数学中的“异想天开”
2019-04-10郜舒竹
□ 郜舒竹
按照百度百科的解释,“异想天开”这一成语具有贬义,指的是在上天的启示和指引下,所产生的不可思议或不符合实际的想法。事实上,如果把“异想(Think Different)”看作是求异的思维过程,与求同的思维过程相对,在思考过程中追求与众不同、不同寻常的想法,那么“异想天开”就应当成为褒义词,是当今学校教育特别是课程与教学应当重视的培养目标。
语文教科书中“司马光砸缸”的故事,寻常的想法是去水中捞人,司马光不同寻常的想法与做法不是去水中救人,而是通过破缸,快捷地实现救人的目的。同样在语文教科书中“围魏救赵”的历史故事,目的是营救赵国,自然的思维是迅速派兵赶往赵国,用武力达到救赵的目的。而孙膑不同寻常的想法是通过围魏,进而救赵,从而不战而胜。这种救人不捞人、救赵不去赵的想法都具有异想天开的特征。数学发展的历史中,类似的例子也很多。
一、赌注分配问题
17世纪的欧洲,盛行博彩业,人们通过下赌注的方式进行诸如掷色子的对弈游戏,根据点数多少分配赌注。当时著名的法国数学家帕斯卡(Blaise Pascal:1623—1662)和费尔玛(Pierre de Fermat:1607—1665)),曾经在相互通信中讨论一个如何公平分配赌注的问题。由于这一问题成为了概率论研究的起源与基础,因此流传至今,被命名为“赌注分配问题”,英译为“Problem of Division of Stakes”或“Problem of Points”。
问题的大意是:甲、乙二人进行对弈游戏,游戏的规则为:每一盘赢者得1分,输者得0分。先得3分者为赢家,获得全部赌注。假设甲、乙二人每人下赌注30元。当第三盘结束时,甲得2分,乙得1分,未分胜负。此时游戏因故停止,二人需要公平分配60元赌注后各自离开。那么此时这60元赌注,应当如何分配最公平?[1]
之前很多人在游戏中都遇到过此类问题,通常的想法和做法是,按照二人已经获得的得分按比例分配。因为此时甲得2分,乙得1分。因此应当把60元平均分为3份,甲分得其中的2份,乙分得其中的1份。也就是甲应当分得60元的三分之二,40元;乙应当分得60元的三分之一,20元。
帕斯卡认为这样的分配并不公平,对弈游戏尚未结束,公平的分配不仅要考虑目前输赢的结果,还要考虑未完成对弈中,输赢可能性的大小。需要进一步研究在目前甲2分、乙1分的情况下,如果对弈过程继续下去,二人胜负的可能性分别是怎样的?
假定二人继续第四盘对弈,会出现两种可能的结果,分别是甲赢乙输和乙赢甲输。如果甲赢,那么游戏结束,甲为赢家,获得全部60元赌注。如果乙赢,二人都得2分,应当平分赌注,每人分别获得30元。因此对于甲来说,第四盘无论输赢,60元中的30元是确定要获得的,而另外30元是由二人第四盘对弈结果决定的,甲、乙二人第四盘输赢的可能性(概率)是相等的,都是二分之一。因此这30元二人应当平均分配,各得15元。因此公平的分配应当是甲得(30+15=)45元,乙得15元。如果用树图,可以更加清晰地看出未完成游戏输赢可能性的大小关系。

图1 输赢可能性示意图
问题的思考中,赌注应当公平分配是没有异议的,因此“公平分配”是解决问题的目标,达到这一目标的方法并不唯一确定。寻常的想法和做法是按照已经获得的得分,按比例分配。而帕斯卡的想法与之不同,是在当前结果的基础上,预测尚未发生游戏结果的可能性大小。也就是说,如果游戏继续下去,甲最终获胜的可能性是四分之三,而不是目前的三分之二;乙最终获胜的可能性是四分之一,而不是现在的三分之一。由于将已经发生的结果和尚未发生的结果的可能性综合考虑,因此使得分配更加公平。
在此基础上,帕斯卡对问题进行了推广。如果在第二盘结束时停止游戏,此时甲两盘全胜得2分、乙两盘全输得0分。那么60元赌注应当如何分配?如果仅按照已有结果分配,此时似乎应当甲获得全部60元赌注,乙得0分自然应当空手而归。但帕斯卡按照预测未完成游戏可能性的方法,得到了不一样的分配结果。
可以设想第三盘游戏的结果,如果甲赢,那么甲三盘全胜,得到3分,游戏结束,甲为赢家,获得全部60元赌注。如果甲输乙赢,那么就转化为前面甲2分、乙1分的情况,甲应得45元,乙应得15元。因此第三盘甲无论输赢,其中的45元是确定得到的,需要平均分配的是15元。因此甲应分得(45+7.5=)52.5元,乙应分得7.5元。
进一步设想,如果在甲1分、乙0分时停止游戏,赌注又应当如何分配?用同样的方法,设想第二盘如果甲赢,那么问题转化为甲2分、乙0分的情况,甲应分得52.5元,乙应分得7.5元。如果乙赢,二人得分相同,应当各自分得30元。因此30元是甲确定得到的,二人应当平分52.5元与30元相差的部分22.5元,因此甲应分得(30+11.25=)41.25元,乙应分得18.75元。
帕斯卡与费尔玛与众不同的异想,不仅解决了困惑已久的问题,而且为数学中可能性问题的研究奠定了基础。概率论中“数学期望”的概念,就源于这一问题的研究。
二、鸡兔同笼问题
在数学课程中,鸡兔同笼问题作为问题解决的教学内容,以各种形式呈现。在2001年出版的《全日制义务教育数学课程标准(实验稿)》以及2011年出版的《义务教育数学课程标准(2011年版)》中,都以案例或例题形式提及鸡兔同笼问题。在小学阶段采用探索规律的方法解决,而初中阶段用代数的方法解决。
鸡兔同笼问题所描述的情境是,二足一头的鸡与四足一头的兔在同一笼中。通常叙述为:鸡和兔在同一个笼子中,总头数为35,总足数为94。问鸡和兔各有多少只?对于这一问题最为经典的算法分别为《孙子算经》中介绍的半足术,以及《算法统宗》中的倍头法。
半足术的算法为:“半其足,以头除足,以足除头即得。”[2]也就是将笼中鸡和兔的总足数94取半成为47。此时相当于笼中的鸡变为一足一头,兔变为二足一头。此时思维中出现的是“一头一足的鸡”和“一头二足的兔”,也就是思维中出现了“是鸡又非鸡”和“是兔又非兔”的情境。
倍头法的算法是:“倍头,减足,折半是兔。”[3]“倍头”就是把总头数35加倍变成70;“减足”是用总足数94减去70得到24;“折半”是取24的一半得到兔子的只数为12。倍头法的第二种算法是先求鸡的只数,算法为“四头,减足,折半是鸡”。“四头”就是用4乘总头数35得到140;“减足”是用140减去总足数94得到46;“折半”是取46的一半得到鸡的只数23。与半足术类似,将鸡与兔总头数加倍,相当于笼中鸡和兔都变成了“二头”或“四头”,同样也出现了鸡非鸡、兔非兔的情境。
按照通常的思维,这种情况是难以理解和解释的。通常的思维一般遵循形式逻辑的基本规律,即同一律(Law of Identity)、无矛盾律(Non-Contradiction Law)和排中律(Law of Excluded Middle)。同一律要求同一思维过程中,任何思维对象应当保持一致,否则就会出现偷换概念的问题;无矛盾律要求任何一个判断或命题不能既真又假,也就是说任何一个判断如果为真,那么其相反的判断一定为假;在此基础上,排中律指的是一个判断或命题或真或假,没有第三种情况。[4]在鸡兔同笼问题的情境中,默认为真的判断至少有如下三条:
判断1:笼中动物非鸡即兔,没有第三种动物。
判断2:凡鸡都是一头二足,不是一头二足的动物一定不是鸡。
判断3:凡兔都是一头四足,不是一头四足的动物一定不是兔。
如果说半足术中所出现的“一头一足”是鸡,“一头二足”是兔,就是承认了判断2和判断3既真又假,违背了无矛盾律。
如果不承认一头一足的是鸡,也不承认一头二足的是兔,就出现了同一思维过程中,鸡和兔概念的属性发生了改变,违背了同一律的要求。如果把一头一足(鸡)以及一头二足(兔)的对象理解为既非鸡又非兔的第三种动物,又违背了判断1所说的笼中动物非鸡即兔,也就是违背了排中律。
因此半足术和倍头法都违背了通常形式逻辑的思维规律,具有与众不同、不同寻常的异想特征。这样的异想不能被认为是错误的思维,而应当看作是对通常逻辑思维的拓展与提升,应当认为是我国历史文化中人们智慧的体现。同时也说明,基于形式逻辑的思维方式是有局限性的。
从人类历史发展的视角看,人的思维形式多种多样。比如,以辩证逻辑为基础的辩证思维,是以辩证唯物主义普遍联系和运动变化的观念为基础,遵循对立统一(Unity of Opposite)的思维规律。认为任何事物的存在,一定伴随着对立一方的存在。对立的双方相互排斥,同时也互为条件、互为因果。对立的双方在一定条件下可以相互转化。在思维过程中,“是”与“非”并非处于截然分离的状态,存在中间地带(Middle Ground)或过渡区(TransitionalArea),思维对象可能同真、共存和相互转化。[5]
半足术中出现的“是鸡又非鸡”的情境,是解决问题过程中思维的产物,是联结“是鸡”与“非鸡”的中间地带或过渡区,作为思维中的存在是合理的。这种是非相容的思维方式可以概括为:是与非可以同地并存、是与非可以同时为真、是与非可以相互转化。因此可以说,半足术与倍头法都是通过不同寻常的异想得到的算法,其中蕴含着辩证思维的特征。
三、将异想融入数学学习
辩证思维对于数学学习中多视角的理解以及方法多样化,具有广泛的实际意义。比如在整数除法运算中,有“余数要比除数小”的规定,与这个判断相对的判断是“余数不比除数小”,其中包含着两种情况,一种是“余数等于除数”,另一种是“余数大于除数”。按照形式逻辑的无矛盾律,如果规定“余数要比除数小”,那么就应当否定余数等于或大于除数的情况。对于2÷2,如果遵循余数要比除数小,那么就是商1余0,写成竖式形式就如图2所示。
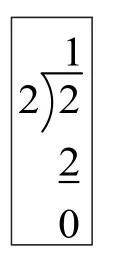
图2
如果按照多视角的辩证思维,可以对此产生异想,余数未必一定小于除数,尝试一下余数等于除数会怎样?将2÷2=1……0改写为2÷2=0……2,也就是商0余2。写为竖式如图3所示。
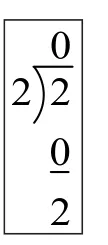
图3
这个竖式(如图4)看起来没有什么意义,如果按照小数除法继续这个竖式的计算,就会得到新的发现,这个异想天开出来的计算过程实际上从除法计算的角度证明了
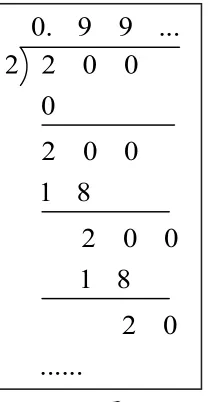
图4
在数学中,许多人为的判断并不是是非分明的,往往具有可能这样,也可能那样的特征。[6]数学学习应当让学生经历这种具有异想特征的思维过程。
再比如在数学课程中,在与“角”有关内容的学习中,有一个“平角”的概念。直观上看平角是一条直线,并不具有通常角的形象,按照形式逻辑的思维方式,就会在思维中产生“平角不是角”的意识。而用辩证思维的眼光看,直观上的“非角”可以与思维中的“是角”并存,用运动与变化的眼光把直线看作是小于180度的角与大于180度的角相互转化需要经过的一个瞬间,这样就实现了“非角”与“是角”的相容和统一。
辩证思维对于探索解题方法,实现方法多样化,也同样具有重要作用。比如小学六年级分数应用题中一个经典的相遇问题:从小红家到小刚家步行需要10分钟,从小刚家到小红家需要15分钟。二人同时从家出发,多少分钟可以相遇?
通常的算法是,设小红家与小刚家之间的距离为“1”,那么小红步行速度为,小刚步行速度为,二人相遇所需要的时间为
这一算法是将思维局限于问题所叙述的“两家之间”的情境。依照是非相容的辩证思维,可以虚拟题目中没有的情境,拓展“两家之间”的情境。比如可以设想,如果二人都按照同样速度步行30分钟,那么小红步行距离就是两家之间距离的3倍,小刚步行距离就是两家之间距离的2倍。说明在相同时间内,小红和小刚的步行距离是3份与2份的关系。如果把两家之间距离视为5份,相遇时小红走了其中的3份,小刚走了其中的2份。那么小红步行时间是10分钟的小刚步行时间是15分钟的,都是6分钟。
这样的思考实质上是将题目中没有的情境视为“有”,在思维中出现了“真情境”与“假情境”的共存与相容,与帕斯卡研究赌注分配问题的思维方式类似,都是虚拟出未发生事件的各种可能性。这样的思维方式符合辩证唯物主义,用运动与变化的眼光看待事物。
如今数学教学倡导变教为学,将以教师教的活动为主的课堂教学改变为以学生学习活动为主的课堂教学。数学教学不再是教师将教科书中单一的、确定的内容传授给学生,而是引导学生积极主动地开展学习活动。在这样的过程中,学生就会产生各式各样异想的结果。
美国苹果公司在题为“异想”的广告词中说:异想的人狂放不羁、不合主流、叛逆传统、制造麻烦、特立独行。但他们是改变世界、推动进步的人。教师在面对学生异想的结果时,如何对待有异想的学生?如何应对学生异想的结果?这将成为数学教学改革需要研究的课题。
