探秘牛顿植树问题
2019-04-10王娜
王 娜
“每行植三株,九株栽十行;种法有多样,请你试试看.”据说这是牛顿曾经提出并思考过的“九树十行”问题.
同学们,动动手,相信你也能给出答案:作一个对称的图形,三横一竖、六根斜线(如图1所示),轻松解决了这个“九树十行”的植树难题.

图1
按实际生活经验,每行3棵,要栽10行,不是需要30棵树吗?现在只有9棵,那有些树肯定应栽在几行的交点上.我们为何会想到画出这样的对称图形?是否有据可依?
我先给同学们普及一下帕普斯定理.
帕普斯定理可以叙述成下面的形式:
如图2,设六边形ABCDEF的顶点交替分布在两条直线a和b上,那么它的三双“对边”所在直线的交点X,Y,Z在一直线上.
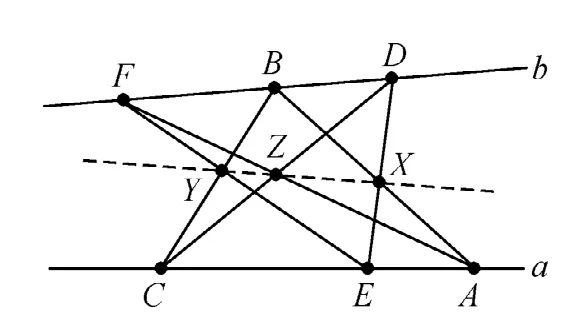
图2
问题初看有点复杂,为了让同学们充分理解定理,我们把问题具体划分为几个步骤进行,同学们可以自己尝试画出这张图形.
三点A,E,C在直线a上,三点D,B,F在直线b上.顺次连结线段AB,BC,CD,DE,EF,FA,得到一条封闭折线ABCDEF,此封闭折线也就是一般意义下的多边形.看六边形的名称ABCDEF,就能知道它的哪两条边是对边.例如,在六边形名称ABCDEF中,字母B和C相邻,说明BC是它的一条边,那么EF就是BC的对边.利用“六边形”和“对边”这两个简单术语,就能概括图2中9个点和9条直线之间的复杂关系.
(注:帕普斯定理的证明可参考《新概念几何》(张景中,2002))
可以看到,图2中有9个点,9条线,每个点上有3条线通过,每条线上又有3个点,由此可直接得到“九树九行”.为了解答现实版的“九树十行”问题,需要在上面“九树九行”的基础上,增加一条新的直线,成为第十条.
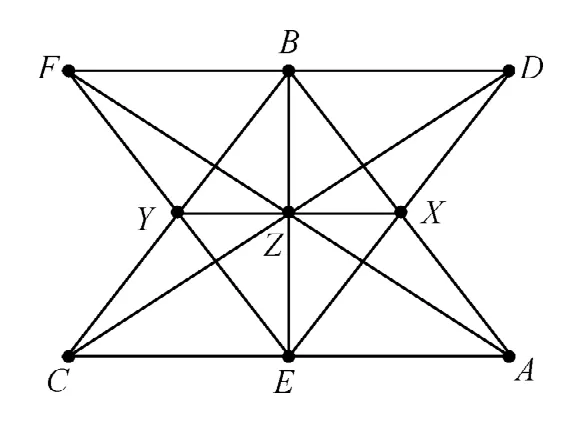
图3
应该怎样安排,才能出现第十条直线呢?
我们回顾文章开头所述问题及图1,显然,运用特殊化的数学思想,让图形具备对称性以后,就完美地出现了第10条直线BE(如图3所示).
继续开动脑筋,如何在一般图形中得到第10条线呢?
如图4所示,可采用下面的办法:

图4
任意作两条直线a和b;
在a上任意取三点A,C,E;
在b上任意取两点B,D;
连结直线AB,BC,CD,DE,AD,记AB与DE的交点为X,BC与AD的交点为Y;
连结直线EY,交直线b于点F;
连结直线FA,交CD于点Z,那么根据帕普斯定理,三点X,Y,Z在一直线上.
这就是解答“九树十行”问题的一般方法.由于两直线a和b的相关位置可以任意变化,六边形顶点在a和b上的排列顺序和距离也可大幅度调节,所以能画出千变万化的解答图形.同学们可以自己尝试操作一下.
