基于灰色马尔科夫模型的上海铁路客运量预测

潘 丽，李 林 （上海理工大学 管理学院，上海 200093）

0 引言

随着科学技术与经济的不断发展，社会的进步改变了人们的出行方式，铁路客运速度的提高，载客量的庞大，使它成为了大多数人出行或旅游交通方式的选择。因此为了方便人们更好的出行，对国家资源进行合理的配置，以及促进铁路部门的发展，实现对铁路客运量的预测变得越来越重要。为了把握铁路运输需求的特征，学者们提出了多种不同的预测模型，但是目前国内外常用的方法还是依赖大量的历史数据，对其进行分析，找出规律，从而做出预测。

国外学者Suryani等建立了一个系统动力学框架模型来预测客运量需求，凭借系统动力学的物理特性和信息流反馈控制连续决策和行动，可以用来模拟、分析和仿真以提高模型的预测水平[1]。Godfrey等应用指数平滑法模型来对客运量进行预测[2]。相对来说，早期的研究方法比较单一，不能结合组合模型的优势。

而国内学者研究客运量的人数更多，常用的预测方法有指数平滑法[3]、Logistic模型[4]、回归分析[5]、支持向量机、神经网络[6]等。这些预测方法具有各自的特点，但是有个共同的特点就是要求预测的历史数据具有良好的平滑度。由于客运量受多种因素的影响，单一的预测方法已经不适合对波动性较大的客流量的预测，往往存在很多弊端。灰色马尔科夫链模型是一种结合灰色系统理论和马尔科夫链理论的预测模型，由于客运量具有明显的灰度特征，因此可以使用灰色模型预测客运量。传统的灰色模型虽然能有效地预测少量数据的序列，但随着数据的增多和波动性的增大，该模型逐渐的失去了它的优势[9]，而马尔科夫模型预测适用于随机波动性较大时间序列中，弥补灰色模型的不足[10]。因此，本研究将上述两种模型相结合，使两者优点互补。

1 建立灰色马尔科夫模型

1.1 灰色GM （1,1）预测模型

灰色GM （1,1）模型是灰色系统理论最常用的一种灰色动态预测模型。是把观测到的数据看作随机时间变化的灰色量或灰色过程，通过累加生成或累减生成局部使灰色量白化，从而建立相应的微分方程模型并做出预测，其建模步骤如下：

（1）假设铁路客运量原始序列为：

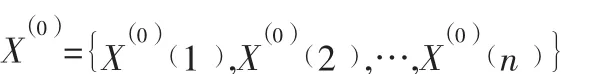
对原始数据进行一次累加得到：

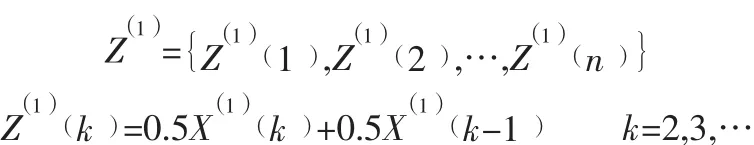
（3） 构建累加序列（X1）的一阶微分方程：

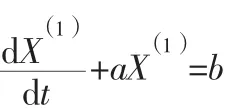
其中：参数a,b可由下列方程式得出：

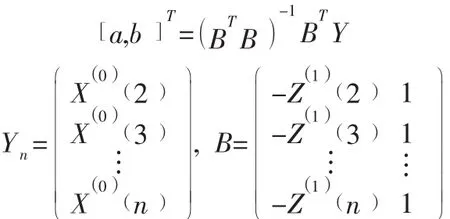
（4）求解微分方程，得到如下的GM （1,1）模型：

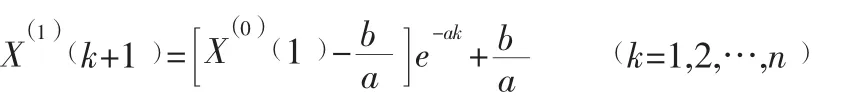
（5）由累加序列还原序列得到：

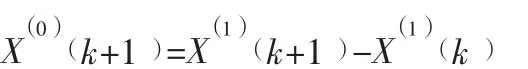
1.2 马尔科夫模型

马尔科夫模型是俄国数学家马尔科夫于1907年提出，后有蒙特卡罗加以发展而建立的一种预测方法，它将时间序列看作一个随机过程，通过对事物不同状态的初始概率与状态之间转移概率的研究，确定事物未来状态的变化趋势。马尔科夫模型可表示为：

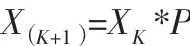
其中：X（K+1）,XK分别为在k+1、k时刻的状态概率向量，P为一步状态转移矩阵。

（1）进行状态区间的划分

根据GM（ 1,1）模型预测的结果，计算原始序列与预测序列的相对误差，并依据状态的集中程度进行划分。

（2）构建状态转移矩阵

由状态Ei经过一个时期转移到Ej的一步转移概率为Pij，将所有的一步转移概率排成一个矩阵，即：

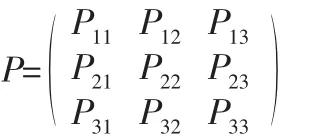
（3） 计算预测值

在状态转移矩阵确定后，根据某一年所处的状态，来预测下一年可能出现的状态，最终求出马尔科夫修正值。

1.3 灰色马尔科夫模型

灰色马尔科夫模型的具体运算步骤：（1）选取预测的时间序列，构建GM （1,1） 模型，得到灰色预测值；（2）计算预测值与实际值之间的相对误差；（3）根据相对误差的大小，从而划分误差范围；（4）计算状态转移矩阵；（5）对灰色预测值进行修正：

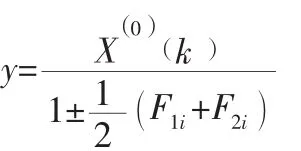
2 实证研究

通过收集资料，得到上海市2007~2016年的铁路客运量数据，并利用灰色GM （1,1）模型求出预测值，再计算其真实值与预测值之间的误差，以及相对误差，得出的结果如表1所示：

2.1 用马尔科夫链修正预测值

根据2007~2016年的上海铁路客运量的实际值和相对误差，划分状态区间，从表1可以看出相对误差的最大值为6.63%，最小值为-5.79%，当灰色预测值与实际值相对准确时，不予修正。即误差范围在（-1%,1%） 之间时，将不对其进行修正，由此划分三个状态区间，分别为E1(-6,-2]，E2(-2,2]，E3(2,7]，如表2所示：

表1 上海市铁路客运量

表2 状态区间划分

2.2 对各年进行状态区间的划分（如表3所示）

表3 相对误差和状态区间

2.3 构建状态转移矩阵

根据各年结果所在状态区间，由状态Ei经过一个时期转移到Ej出现的次数除以Ei的次数，得到如下的一步状态转移矩阵和二步状态转移矩阵：

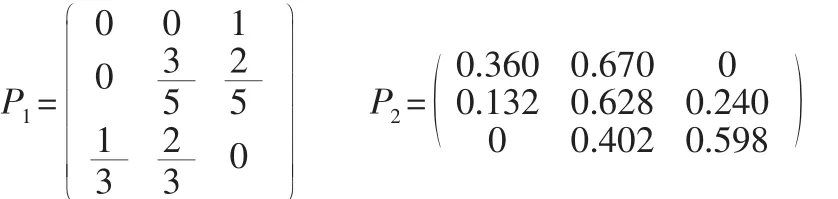
2.4 计算预测值

由状态转移矩阵及各年份所处的状态，可以求出上海市铁路客运量的马尔科夫预测值。以2008年为例，则可以看出2007年的相对误差处于E2状态，经过一年的转换，转换为E2和E3的概率分别为3/5和2/5，则认为2008年的状态最有可能处于E3状态。运用GM （1,1）模型求得的2008年的预测值为49.69，则利用灰色马尔科夫进行修正的预测值为50.60，运用同样的方法得到的其他年份的预测值如表4所示：

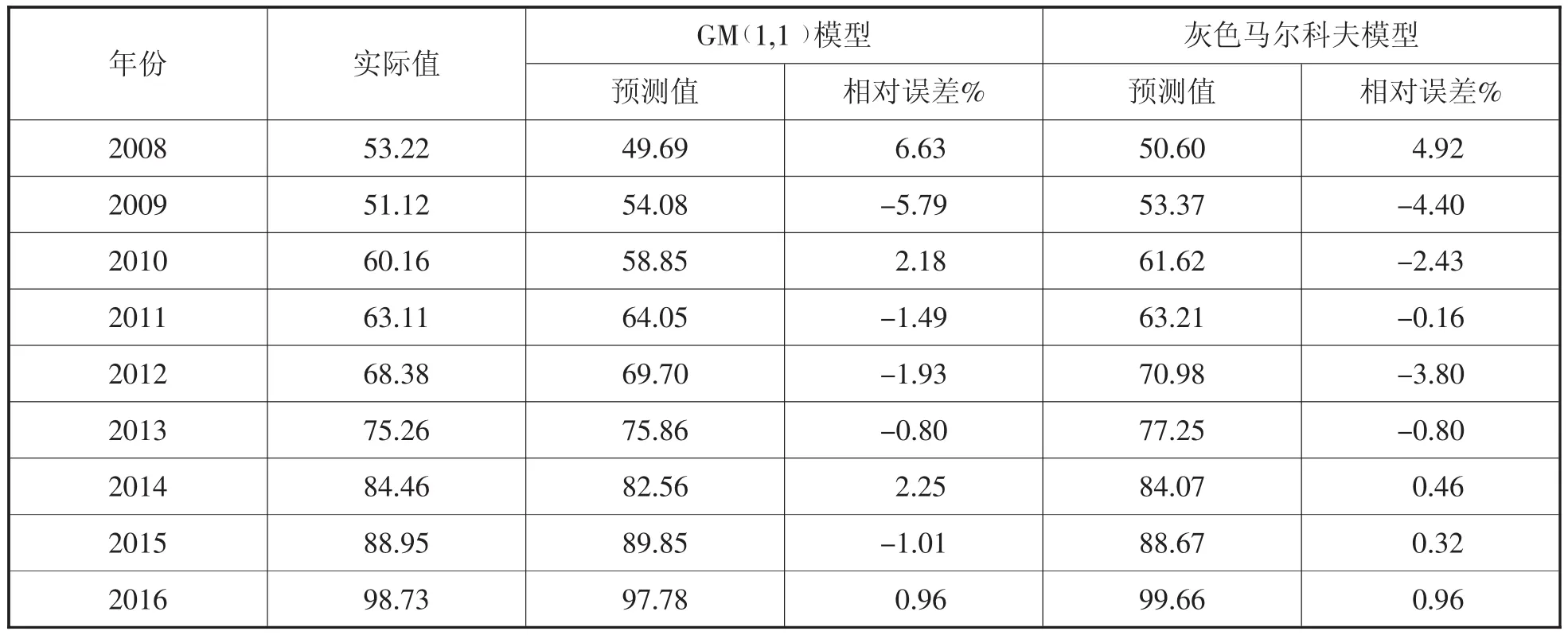
表4 灰色拟合值与马尔科夫拟合值

从上述的预测结果可以得出：利用单独的灰色模型求出的误差是2.56%，利用灰色马尔科夫模型求出的误差是2.03%，对比两种方法，降低了误差范围，说明灰色马尔科夫模型的预测结果更好，更加适用于对客运量的预测。而且可以看出，灰色马尔科夫预测值与实际值的拟合度较高，波动性一致，其参考价值高，利用灰色模型能看出哪些年份的预测值具有较大的变化趋势，而从图1中可以看出灰色模型是一条相对平滑的曲线。不能反映实际值的波动。

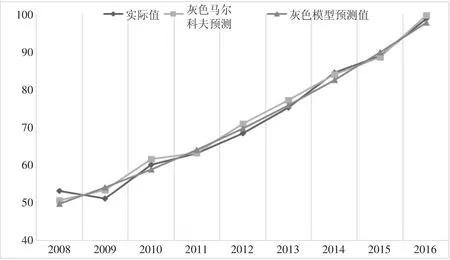
图1 灰色马尔科夫预测值与实际值和灰色值的对比曲线

2.5 由灰色马尔科夫模型预测2017～2020上海客运量的预测值如表5所示：

表5 灰色马尔科夫预测值

从预测的结果来看，上海铁路客运量的增长是必然趋势，趋于一种不稳定的螺旋式增长。铁路部门自发展以来，以其独特的优点吸引越来越多的乘客。本文利用灰色马尔科夫模型，充分考虑了铁路客运量的增长趋势和随机变动趋势，并将两个方面加以考虑，使预测效果更加具有可信性，通过合理利用可以对铁路客运决策产生积极影响。

3 结论

为提高客运量准确性，把握客运量发展趋势，从而更好地帮助铁路行业和相关企业的决策提供科学依据。无论是在铁路还是公路等方面，客运量的预测都是非常重要的手段，在信息发展迅速的今天，客运量的预测能够为相关的部门提供合理地决策依据和建议。

（1）灰色马尔科夫在上述各列表的相对误差的绝对平均值都小于5%，预测结果精确度较高，且效果比灰色预测法更加稳定。

（2）对于实际值序列模型改变明显时，组合预测法的结果优于单一预测法结果，从表4可以明显看出，灰色马尔科夫模型一方面吸收了灰色预测法的有效信息，另一方面也利用了马尔科夫模型的优势，降低了数据的随机性。

（3）但是灰色模型作为一种理论的预测方法，其结果未考虑到客运量变化的主要影响因素。实际情况远远比模型更加复杂，其结果往往起参考作用。通过进一步结合马尔科夫模型，提高精确度。