基于改进蚁群算法的AGV路径研究

何成伟，茅 健 HE Chengwei,MAO Jian

（上海工程技术大学 机械与汽车工程学院，上海 201620）

0 引言

AGV已是现代物流工厂重要的运输设备，在应对越来越复杂的物流环境中，需要解决物流工程与任务复杂度的增加，AGV智能化的需求也越来越高，实现AGV的自主化也是国家实现2025计划，工业4.0智能制造的重要部分。传统的最优路径规划方式有基于A*算法[1]，Dijkstra算法[2]，但是都有着计算量大，收敛速度慢，不具备实时性的弊端。近年来，神经网络[7]、蚁群算法[4]和遗传算法[3]也陆续应用到路径规划中。在这些方法中，神经网络因其具有良好的自适应和学习优化能力，但是其泛化能力弱，不具有普适性；遗传算法有着较强的搜索能力，改进遗传算子，引入适用度权重系数[5]，可以很好地寻求全局最优解，但是效率低；蚁群算法有着很强的启发性和稳定性，许多学者对蚁群算法有着深入的了解，使用蚁群算法结合Dijkstra算法规划AGV初始路径，引入节点随机选择机制得到最优路径[6]，或是通过更改启发函数，算法中引入全局信息，得到全局的最优解[7]。

本文针对单台AGV在复杂物流车间运输过程中如何规划最优路径的问题，研究了基于改进蚁群算法的启发函数和信息素挥发系数，利用引入全局信息，设计避障因子和构造路径光滑参数三个方面进行优化。搜索到保证路径光滑的情况下，得到的最短路径。仿真结果表明，本算法具有较好的最优路径距离，且具有更好的避障能力，耗时较小，更适合于复杂的工厂环境。

1 构造AGV作业环境

在AGV路径规划中，首先需要建立AGV运输环境模型。常有可视图法，栅格法和无向网络图。根据实际物流车间运输的情况，本文应用MAKLINK无向网络图，按如下规则构造AGV可移动路径。

（1）将移动的AGV看作是质点。

（2）将障碍物向各个方向膨胀，将其抽象为凸多边形。即使是规划的AGV沿着凸多边形边缘行走也不会与真实的障碍产生碰撞。

（3）每条自由连接线不能穿过障碍物。

（4）连接线的端点可以是障碍物的凸多边形的顶点，或者是自由空间的边界上的点。

（5）取每条连接线上的中点，作为AGV可行驶的节点。

图1 构造MALINK自由路径

图1中S—AGV行驶起点；T—AGV行驶终点；图中细线封闭凸多边形为障碍物。将节点相互两两相连，作为本文AGV路径规划的无向网络图。

2 改进蚁群算法

根据传统蚁群算法，第k只蚂蚁从节点i出发到达下一个节点j转移概率为：

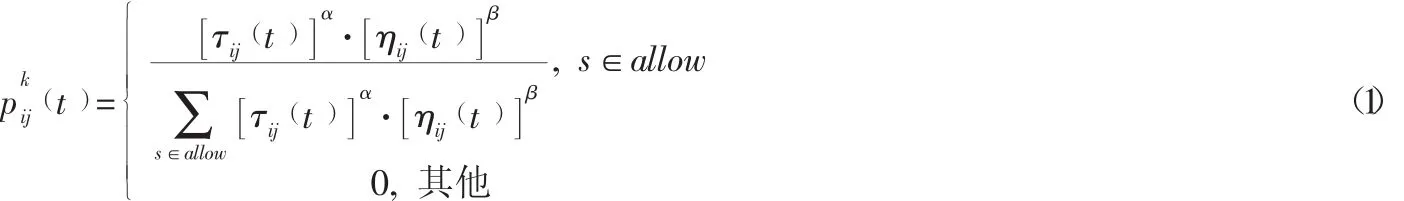
式中：allow为节点i出发到其余所有的节点j的集合；为蚂蚁在路径i到j节点上留下的信息素浓度；ηij（t）为节点i到节点j的转移期望值，是节点j的启发函数；α为信息素浓度对转移概率的影响因子；β节点i到节点j的期望值对转移概率的影响因子。

启发函数ηij（t）的计算公式如下：

式中：dij为节点i与节点j之间的距离值。

若节点i和节点j的距离越短，启发函数的值就越大，节点i到节点j的转移概率也越大。

从上述分析来看，蚁群算法只考虑了相邻节点与节点的距离，没有考虑节点之间是否存在障碍。

2.1 引入避障因子和全局信息

当两个直线段有交点时，即认为节点i和节点j之间有障碍物G存在。即当xg2＞xa＞xg1，xi＞xa＞xj时，节点i和节点j存在障碍物。

计算直线方程lij各参数，计算得到直线lij,lg。

A点（xa,ya）是上述两直线产生的交点，即可得：

各坐标点的大小关系，构造避障函数 γij（t），γij（t）∈[0,1 ]。构造 γij（t）的计算公式如下：

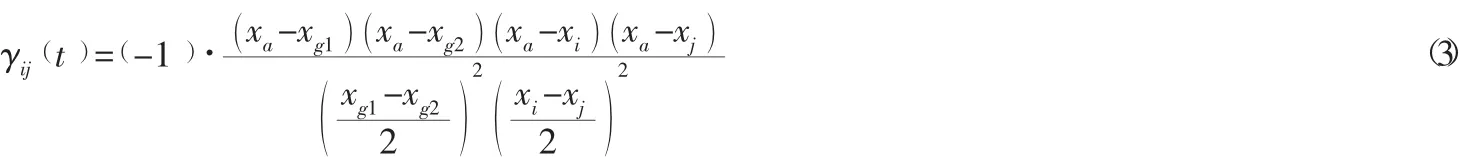
根据式（3） 可见，当满足节点i和节点j之间有障碍物时，的值为负；当节点i和节点j之间无障碍物时，γij（t）的值为正。所以，当存在障碍物时，可得启发函数）的值比原来大幅减小，并通过启发因子β放大，其转移概率大幅下降，此时算法将选择邻近其他无障碍节点作为下一个路径点。

式（4）中，djT为下一个节点到终点T的直线距离。ωj为引入的动态全局优化因子，ωj∈ 0,[ ]1 。ωj的计算公式为：

式（5）中，Mcurrent为从起点运动开始计算的已经通过的自由空间中节点数；Mmax为所有自由空间中节点数量。

当算法刚刚开始，通过计算当前的节点数和所有节点数的比值，ωj的值很小，启发函数ηij（t）的值很大，搜索范围内的转移概率将被放大，可以提高算法的准确性；当蚁群算法逐渐搜索到后期，ωj的值逐渐变大，启发函数）逐渐变小，使蚁群算法收敛速度增加。

将式（4）代入式（1）中，得到改进后的蚁群算法转移概率计算公式：

2.2 路径光滑因子

根据传统蚁群算法运算结果，规划的AGV路径存在有突变节点，即AGV在行驶中速度与加速度变化较大，行进方向有较大突变。带来的后果是按照不光滑路线行驶的AGV，时常需要改变较大的行驶角度，致使在转动的过程中AGV损耗更多的电量和时间。由此，在改进蚁群算法转移概率目标函数时，考虑将路径光滑作为一个参数，构造路径光滑因子。

选取一条AGV行驶路径，取其中三个连续的路径节点A、B、C。如图2所示，夹角φ为后一时刻AGV行驶线段的延长线与当前路径方向的夹角。

为了使规划的路径近似光滑，即是AGV方向转角较小，所以φ的角度在0~90°之间。构造路径光滑参数λ和路径光滑因子f，其计算公式如下：

图2 路径光滑示意图

如式（7）所示，λ作为路径光滑参数，反应了前后两个时刻的规划路径节点是否满足近似光滑条件，即φ的值不超过0.5π，则λ∈[0,1] 。若前后两个时刻规划路径节点不满足近似光滑，即φ的值超过了0.5π，则λ的值超过1，认为AGV行驶在这一节点不光滑。

式（8）为光滑因子f函数表达式，含有路径光滑参数λ，光滑因子f的值决定了AGV已行驶路径的光滑程度。当f的值大于1时，说明路径不光滑，将重新选择路径点；当f的值小于1时，左右说明路径较为光滑，平均每个节点的φi都小于90度，满足路径光滑条件。式中的Mcurrent是指这一条路径上的已经走过的节点数，即AGV行驶中需要变换方向的节点。

根据全局信息因子ω，避障因子γ和光滑因子λ，改进的转移概率计算公式如下：

避障因子（γij）t通过正负值差异来判断是否在下一时刻有障碍物，为保证避障因子在整个转移概率公式中起作用，即保证的分子不为双数。如上式所示，在路径不是很光滑的情况下，则f的值变大，的值就会变小，从而整个转移概率在避障因子计算后，再通过比较大小得出最光滑的路径。

2.3 信息素更新策略

原蚁群算法中，通过构造关于信息素浓度和时间的函数关系来达到这一功能。原下一时刻信息素浓度的计算公式如下：

式 （10） 中，τij（t）为t时刻节点i到节点j路径上的信息素浓度，τij（t+1 ）为t+1时刻节点i到节点j路径上的信息素浓度；（1-ρ）为信息素残留系数；ρ为信息素挥发系数。

当ρ的值较大时，信息素挥发加快，对应路径上的信息素残留浓度小；当ρ的值较小时，信息素挥发缓慢，对应路径上的信息素残留浓度大。

针对信息素挥发系数ρ，同样引入避障函数γij（t），改进更新的信息素挥发系数ρ（t）为：

式（13）中，ρ0为初始信息度浓度；Ncurrent为当前迭代次数；Nmax为算法最大迭代次数。

引入避障函数γij（t）之后，改进的信息素挥发系数ρ（t）在有障碍的路径上挥发率大幅增加，使错误节点的信息素残留少，降低了错误节点的转移概率。

在算法开始初期，经过的节点数较少，ρ（t）信息挥发系数较小，各节点上的信息素残留浓度较大，降低了算法陷入局部最小值的概率；随着算法到后期，经过节点数增多，信息素挥发系数增大，算法收敛加快。将式（13）代入式（10）中，得到改进后的随时间变化的信息素更新方法为：

改进后蚁群算法流程图如图3所示。

3 仿真实验分析

为了验证改进蚁群算法在AGV全局路径规划中的有效性，本文根据广东某物流企业的实地生产线，构建40m×50m的物流工厂环境模型，令AGV的起点为S（ 5,3 5 ），AGV的目标点T（ 45,5）。在空间中含有4个凸多边形作为障碍物。

在蚁群算法初始化中，设定信息素浓度Q=10，信息素挥发系数初始值ρ0=0.1，信息素初始值τ0=0.004。蚁群中的蚂蚁数量为20，启发函数的启发因子数β=5，信息素影响因子为α=1，最大迭代次数为Nmax=100。

基于上述初始化的参数设置，在应用传统蚁群算法之前先应用A*算法，目的是利用A*算法为传统蚁群算法先运算出避开障碍的节点。

改进蚁群算法分别进行实验，搜索得到的最优化路径分别如图4、图5和收敛速度曲线如图6、图7所示。

图4和图5中的粗实线为算法得到的最优化路径。改进算法和传统蚁群结合A*算法的路径光滑因子f的值分别为0.20和2.4。可见，传统蚁群算法路径论光滑程度不如改进蚁群算法的路径，图5中在节点P30、P6和P12处有突变，改进蚁群算法路径仅在节点P12处出现突变。由图6和图7可见，改进蚁群算法在迭代次数为43左右收敛，而传统蚁群算法在迭代次数60左右收敛。改进算法收敛速度快于传统算法。

所示的仅为一次实验的结果，在初始化参数设置相同的情况下，对上述两者分别进行50次仿真实验。得到实验结果在图8和图9中所示，经过计算，改进蚁群算法的平均最优路径为60.31m，传统蚁群算法为68.24m，改进算法比传统蚁群算法短；改进蚁群算法的平均达到最优路径的迭代次数为46次，就已经收敛，传统蚁群算法为迭代75次后收敛，改进算法比传统蚁群算法达到最优路径的迭代次数较少。各评价系数平均值如表1所示：

4 结束语

本文提出了基于改进蚁群算法中的AGV路径规划方法，在启发函数中引入了避障条件，优化路径光滑，构造全局信息因子，来应对AGV面对的复杂地形，找寻避开障碍的光滑最优路径，达到保证安全、提高作业效率的目的。通过实验仿真，验证了该改进算法不仅具备避开障碍的能力，且规划的最优路径和迭代次数均优于传统蚁群算法结合A*算法。研究结果将提高AGV应用的自动化程度，对未来AGV在应对复杂物流环境有着一定的价值。

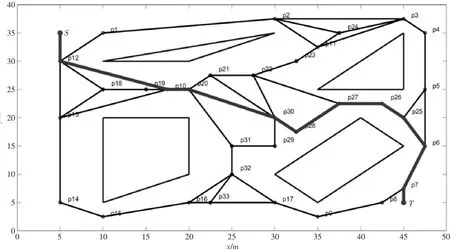
图4 传统蚁群结合A*算法规划结果

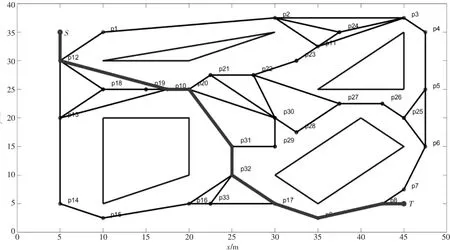
图5 改进蚁群算法规划结果

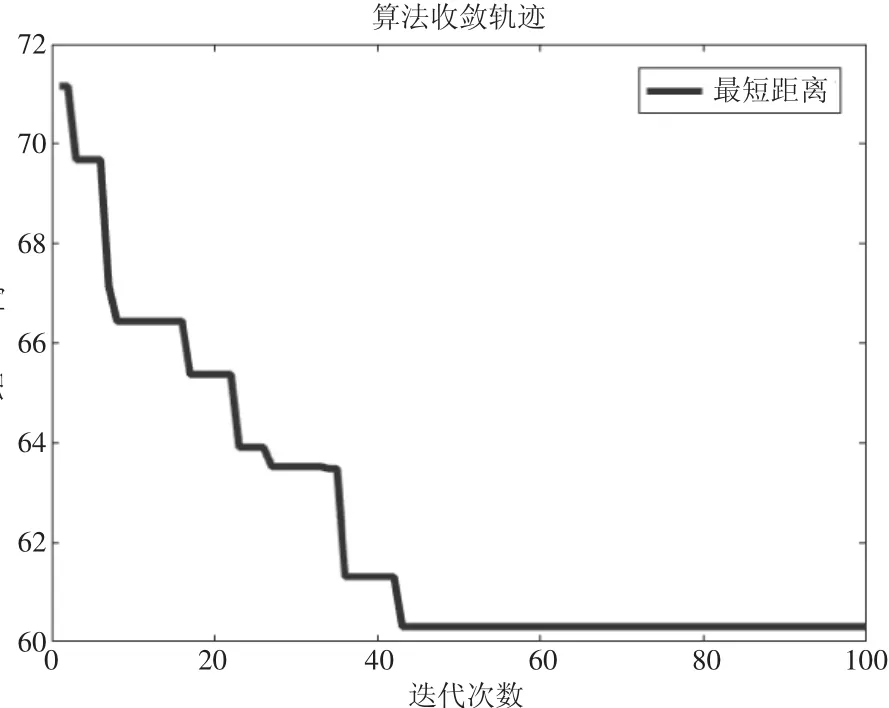
图6 传统蚁群迭代次数

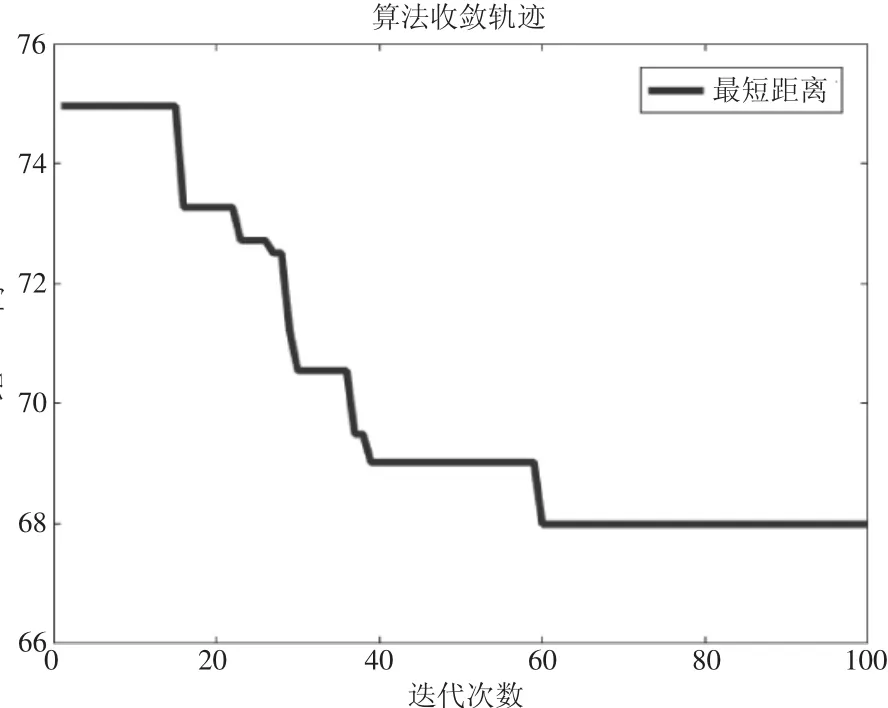
图7 改进蚁群算法迭代次数

表1 各评价参数平均值

图8 两种算法最优路径距离

图9 两种算法最优迭代次数

[2] 汤红杰，王鼎，皇攀凌,等.优化Dijkstra算法在工厂内物流AGV路径规划的研究[J].机械设计与制造，2018(5)：117-120.