函数与导数的综合应用测试题（B卷）

2019-04-09河南省许昌高级中学何晓亚

中学生数理化(高中版.高考数学) 2019年3期

关键词：切线实数单调

■河南省许昌高级中学何晓亚

一、选择题

1.如图1，y=f(x)是可导函数，直线l：y=kx+2是曲线y=f(x)在x =3 处的切线，令g(x)=xf(x)，g "(x)是g (x )的导函数，则g "(3)=( )。

A.—1 B.0C.2 D.4

图1

2.若函数f(x)=2 sinx(x∈[0，π))的图像在切点P处的切线平行于函数g(x)=的图像在切点Q处的切线，则直线P Q的斜率为( )。

3.已知函数f(x)=a x3—3x2+1，若f(x)存在唯一的零点x0，且x0＞0，则a的取值范围是( )。

A.(2，+∞) B.(1，+∞)

C.(—∞，—2) D.(—∞，—1)

4.定义在区间(0，+∞)上的函数y=f(x)使不等式2f(x)＜x f "(x)＜3f(x)恒成立，其中y=f "(x)为y=f(x)的导函数，则( )。

5.定义在R上的可导函数y=f(x)满足f(1)=1，且 2f "(x)＞1，当x∈时，不等式f(2 c o sx)＞的解集为( )。

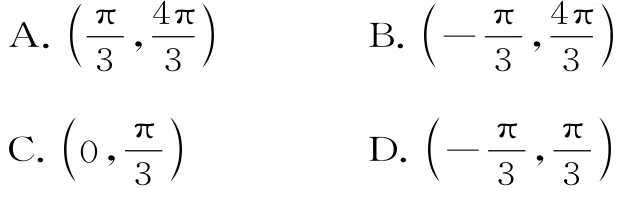
6.若函数f(x)=的最大值为f(—1)，则实数a的取值范围为( )。

A.[0，2 e2] B.[0，2 e3]

C.(0，2 e2] D.(0，2 e3]

7.已知函数若x=2是函数f(x)的唯一的极值点，则实数k的取值范围为( )。

A.(—∞，e] B.[0，e]

C.(—∞，e) D.[0，e)

8.若定义域为R的单调递增函数y=f(x)对于任意两个不相等的实数m，n都有成立，y=f "(x)为函数y=f(x)的导函数，则f(a+1)—f(a)，f "(a)，f "(a+1)的大小关系为( )。

9.对于三次函数f(x)=a x3+b x2+c x+d(a≠0)，给出定义：设y=f "(x)为函数y=f(x)的导数，f″(x)是f "(x)的导数，若方程f″(x)=0有实数解x0，则称点(x0，f(x0))为函数y=f(x)的“拐点”。经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心。设函数，则

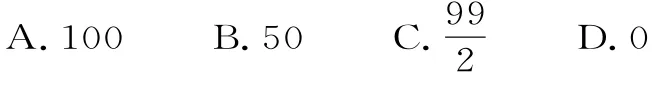
1 0.已知函数f(x)=a x2—4a x—l nx，则f(x)在（1，3）上不单调的一个充分不必要条件是( )。

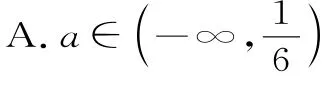
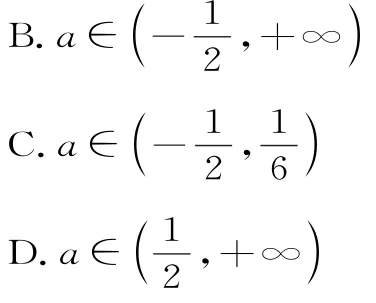
1 1.已知函数f(x)=(x∈R)，若关于x的方程f(x)—m+1=0恰好有3个不相等的实数根，则实数m的取值范围为( )。

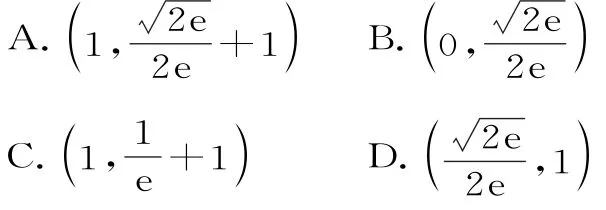
1 2.设直线l1，l2分别是函数f(x)=图像上点，处的切P1P2线，l1，l2垂直相交于点P，且l1，l2分别与y轴相交于点A，B，则△P A B的面积的取值范围是( )。

A.(0，1) B.(0，2)

C.(0，+∞) D.(1，+∞)

二、填空题

1 3.若函数f(x)=x2—ex—a x在R上存在单调递增区间，则实数a的取值范围是____。

1 4.若函数a x+b)的图像关于直线x=—1对称，则f(x)的最大值为____。

1 5.已知函数其中e是自然对数的底数。若f(a—1)+f(2a2)≤0，则实数a的取值范围是____。

1 6.若对任意的x∈D，均有g(x)≤f(x)≤h(x)成立，则称函数f(x)为函数g(x)到函数h(x)在区间D上的“任性函数”。已知函数f(x)=k x，g(x)=x2—2x，h(x)=(x+1)(l nx+1)，且f(x)是g(x)到h(x)在区间[1，e]上的“任性函数”，则实数k的取值范围是____。