导数创新题追根溯源
2019-04-09河南省许昌高级中学杨艳齐
■河南省许昌高级中学 杨艳齐
在近几年全国及各地的高考试题中,创新型试题不断出现,给人耳目一新的感觉,究其实质,基本是以函数的图像性质和导数为平台,构造出新颖的题目,而且突显“能力立意、合理区分”的命题追求。这就要求同学们在熟练掌握函数图像、函数性质、导数应用等基础上认真阅读题目,理解题设要求和符号含义,收集整理有效信息,将问题适时转化为已知问题加以解决。
例题已知函数f(x)与g(x)的公共定义域为I,函数h(x)满足:对任意x∈I,点(x,h(x))与点(x,g(x))均关于点(x,f(x))对称。若f(x)=al nx—x2+a x(a>0),g(x)=ex+1,其中e=2.7 1 82 8…为自然对数的底数。有下列命题:
①当a=1时,曲线y=h(x)在x=1处的切线斜率为—e—2;
②当a=1,x∈[1,+∞)时,函数h(x)的值域为(—∞,—e—1];
③若函数f(x)在(0,2)内不单调,则a的取值范围为(0,2);
④设函数F(x)=bl n[g(x)—1]+f "(x)+2x—a,其中b>0,f "(x)为f(x)的导函数。若O为坐标原点,函数F(x)的图像为C,则对任意的点M∈C,都存在唯一的点N∈C,使得t a n∠MON=b。
其中真命题的个数为( )。
A.1 B.2
C.3 D.4
详细解答:本题主要考查导数在函数研究中的应用。
由题意可知I=(0,+∞),h(x)=2f(x)—g(x)=2al nx—2x2+2a x—ex—1(x>0),所以h "(x)=
命题①,当a=1时,h "(1)=2—4+2—e=—e,故命题①错误。
命题②,当a=1时,由①知h "(1)=—e,又因为x∈[1,+∞)时,h″(x)=—2x—2—4—ex<0,所以h "(x)<h "(1)=—e<0,h(x)在[1,+∞)上单调递减,所以h(x)≤h(1)=—e—1,故命题②正确。
命题③,由题意可知f "(x)=a—2x+x a=0在x∈(0,2)内有解,又因为a>0,所以f "(x)在x∈(0,2)内单调递减,所以有f "(0)·f "(2)<0。又因为)>0,故f "(2)<0,即解得故命题③错误。
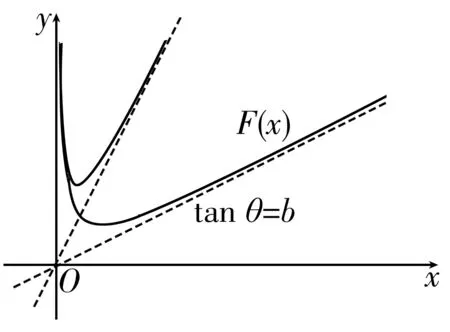
图1
命题④,化简整理得F(x)其大致图像如图1,因为对勾函数的渐近线的斜率为t a nθ=b,由图可知,当θ>4 5°时,不存在符合题意的点N,故命题④错误。
故本题正确答案为A。
易错项分析:本题易错点是利用导数判断单调性及求极值时没有注意对参数的讨论,没有考虑利用数形结合的方法解决问题,不熟悉对勾函数的渐近线性质。对于基本函数,我们一定要掌握其性质。
归纳总结:题设中的新定义涉及三个函数,其中有了f(x)和g(x)之后,h(x)就被确定了。我们逐一分析这三个函数。
f(x)是由对数函数和二次函数组合而成的函数,但是含有参数a,也就是说,f(x)的解析式随a的变化而变化。幸运的是,题中给出了关于g(x)的函数方程。不要急着研究h(x),先看4个命题。
命题①和②都是在a=1时研究h(x)的性质,所以我们首先研究当a=1时h(x)的解析式。当a=1时,f(x)=l nx—x2+x,又g(x)=ex+1,由题意,任取x0>0,则点(x0,h(x0))与点(x0,g(x0))关于点 (x0,f(x0))对称,所以故h(x0)=2f(x0)—g(x0)=2 l nx0—2+2x—ex0—1。
所以h(x)=2 l nx—2x2+2x—ex—1。
下面逐一验证命题①,②。
①h "(x)=2—4+2—e=—e,故①错误。
②当x≥1时,h "(x)=—4x+2—ex<0,故h(x)在[1,+∞)上单调递减,所以h(x)≤h(1)=—e—1,值域为(—∞,—e—1],故②正确。
接着看命题③。
③若函数f(x)在(0,2)上不单调,则f "(x)在(0,2)上有变号零点。
因为f "(x)=—2x+a,则—2x+a=0在(0,2)内有解且无重根,把a分离出来,得
构造函数u(x)=(x∈(0,2)),则>0,故u(x)在(0,2)上单调递增,u(0)=0,u(2)=,所以0<a<故命题③错误。
最后看命题④。
④F(x)=bl n(ex+1—1)+,其中b>0,a>0。
F(x)就是我们通常所说的“对勾函数”(有的地方叫双勾函数,耐克函数)。对勾函数的图像其实是双曲线,如果换一个角度去看的话,和我们在圆锥曲线中学到的双曲线并 曲曲无 线线二
图,的就致2对有。中称渐的轴近虚。线线既。就然是是双双
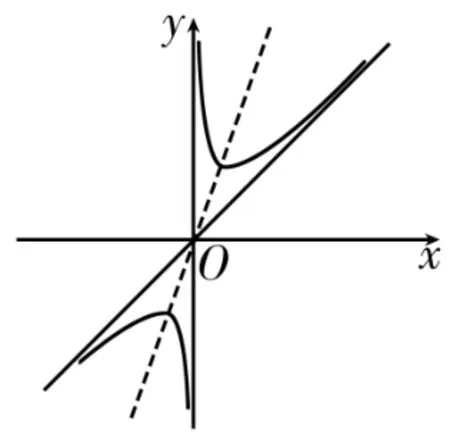
图2
以y=x+为例。
当x→0时,函数图像无限趋近于y轴,当x→+∞时,函数图像无限趋近于直线y=x,故这个函数的图形有两条渐近线x=0和y=x。以此结论作推广,函数(a,b>0)有渐近线x=0和y=a x。
回到命题④。
F(x)=b x+有渐近线y=b x,其中b就是渐近线的斜率。
命题④的意思是说,总存在满足题意的点M,N。
我们不妨从特殊值出发,对b进行取值,验证几个试一试。单则的函
不数数值的妨。图取取像最b如常=图1见3,a、。最=1简,一钝支角
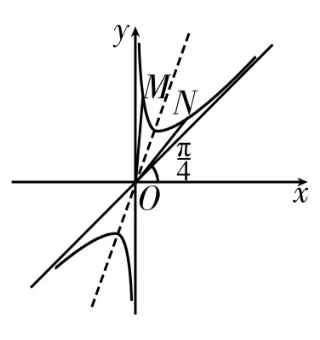
图3
显双,正然曲切,线当值时M为,∠,负NM值O不,N不在同为可能为1,不符合题意。
当M,N在同一支双曲线上时,从图中能够看出,∠MON始终小于
故当b=1,a=1时,不存在M,N两点,使得t a n∠MON=b。命题④错误。
所以真命题只有1个,故选A。
练习:对于函数f(x)和g(x),设a∈{x∈R|f(x)=0},β∈{x∈R|g(x)=0},若存在α,β,使得|α—β|≤1,则称f(x)与g(x)互为“零点关联函数”。若函数f(x)=ex—1+x—2与g(x)=x2—a x—a+3互为“零点关联函数”,则实数a的取值范围为( )。