基于PSO-Simulink联合仿真法的自动变速器换挡优化

于文涛，李晶华，刘 阳

（1.天津职业大学汽车工程学院，天津 300413；2.天津云联科技有限公司，天津 300300）

自动变速器因具有易于驾驶、换挡平稳和通用性良好等优势，在我国汽车制造业得到了广泛的应用和发展[1]。随着人们对汽车安全性、制动性、传动性、经济性、舒适性、驾驶性及智能化要求的不断提高，汽车设计及制造者对自动变速器的品质提出了更高的要求[2]。自动变速器会随路面工况的不断变化而进行即时切断，从而发生换挡。戴卓等[3]基于整车动力学方程和最小二乘法建立了7速双离合自动变速器动力模型，模拟出自动变速器坡道换挡所需的道路坡度与整车质量之间的数学关系。孙贤安等[4]基于XPC平台建立了干式双离合器式自动变速器控制系统的硬件仿真平台，该平台可有效地模拟出普通型和修正型换挡规律。孙慧芳等[5]基于模糊控制理论建立了实际驾驶环境和换挡现象之间的关系模型，确定了换挡规律修正因子，该模型可优化和指导驾驶员行驶控制，减少不必要换挡操作。史炎等[6]使用2个行星齿轮排构建了一种新型自动变速器——双倍挡变速器，通过增加啮合齿轮数量，可增加8速、12速和16速的变挡，并利用SIMPACK软件建立双倍挡变速器的2个挡位启动、换挡及制动工况模型。

换挡决策可分为性能指标最优原则和驾驶员经验或专家系统智能换挡原则。性能指标指最优原则需要精准的数学模型为求解条件，但当车辆实际运行条件与换挡规律求解存在较大差别时，其模型难以及时获得最优解。神经网络理论是智能专家换挡求解的一种新方法。该方法是根据所处环境和行驶状态建立最终的专家系统库，随后根据车辆所处环境和行驶状态来获得最佳换挡参数[7]。目前，我国变速器换挡主要集中于理论研究，处于实验的初级阶段，尚未与人工智能相结合[8]。本文基于粒子群算法（particle swarm optimization，PSO）建立某车型的自动变速换挡过程中的脚踏油门开度、挡位、车速及发动机转速之间的关系模型，为评价该车型的自动变速器的品质提供最优化的换挡条件及理论指导。

1 模型简介

1.1 汽车传动系统

典型汽车传动系统工作示意图如图1所示。驾驶员依据外部环境（人流、路况和信号灯等）和自身车况条件（油门开度、挡位、发动机功率），通过脚踏油门程度、变换挡位和脚踏制动踏板的方式依次直接或间接地调整或控制液力变矩器和齿轮变速器机构，实现对汽车动力系统的控制，即实现了对汽车速度的控制。在这个过程中，变速器结构通过换挡调节传动系统输出力矩，而变速器的传动比为下一时刻车辆变速器的需要输出力矩的放大或缩小倍数[9]，因在车辆连续换挡的过程中，变速器本身输出的力矩已得到了放大或者缩小，故其输出的力矩大小为车辆在该挡位下的传动比。

图1 典型汽车传动系统工作示意图

1.2 PSO算法

PSO算法是基于生物种群行为特征的一种新型群体智能优化算法。算法中的每一个粒子都代表问题的一个潜在解，每个粒子对应一个由适应度函数决定的适应度值。该算法用位置、速度和适应度三者指标表征该粒子的特征，使用度值由适应度函数计算获得。粒子在解空间运动，追踪个体极值PBest和群体极值GBest更新的个体位置。粒子每更新一次位置，就依次计算使用度值，通过比较新粒子的适应度值和个体机制，群体极值的适应度更新个体极值PBest和群体极值GBest位置。

假设在一个D维的搜索空间中，由n个粒子组成的种群 X=（X1，X2，X3，X4，…，Xn），其中第 i个粒子为一个 D 维的向量 Xi=（Xi1，Xi2，Xi3，…，XiD）T，代表第 i个粒子在D维搜索空间中的位置，亦代表问题的一个潜在解。根据目标函数可计算出每个粒子位置Xi对应的使用度值。第 i个粒子的速度为 Vi=（Vi1，Vi2，Vi3，…，VnD）T，其个体极值为 Pi=（Pi1，Pi2，Pi3，…，PiD）T，种群的全局极值为 Pg=（Pg1，Pg2，Pg3，…，PgD）T。在每一次迭代过程中，粒子通过个体极值和全局极值更新自身的速度和位置，更新公式为：

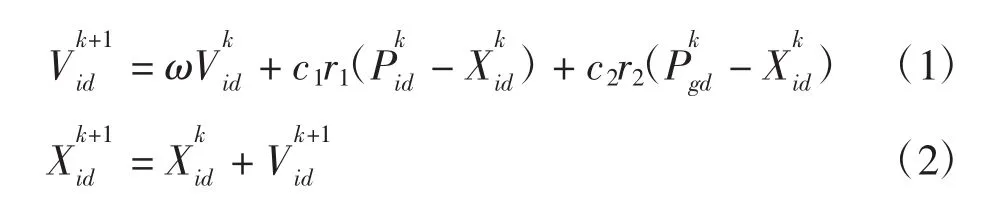
式中：ω 为惯性权重；d=1，2，…，D；i=1，2，…，n；k 为当前迭代次数；Vid为粒子的速度；c1和c2为非负的常数，称为加速度因子；r1和r2为分布于[0，2]之间的随机数。为防止粒子的盲目搜索，一般建议将其位置和速度限制在一定的区间[-Xmax，Xmax]和[-Vmax，Vmax]。

1.3 模型构建

PSO-Simulink法的自动变速器换挡优化流程如图2所示。

图2 PSO-Simulink法的自动变速器换挡优化流程

2 实验结果及分析

2.1 实验条件

实验车为别克凯越（该车已经鉴定，且在鉴定有效期内），在国道开展试验。采用某公司自行研制的车辆自动记录仪检测油门开度、车速及发动机转速数值。车辆换挡过程为1→2挡，2→3挡，3→4挡，4→3挡，3→2挡，2→1挡，在该过程中测试节气门分别显示参数为 0，5%，25%，35%，40%，50%，90%，100%时的车速。测试车速分别为20～180 km/h时的液力变矩器数值。分别利用PSO-Simulink算法和单纯的Simulink算法计算模型所用的运算时间和迭代步数。

2.2 仿真实验结果

基于PSO-Simulink算法和单纯的Simulink算法，分别建立换挡操作模型，模型的输入层为换挡过程中的挡位、换挡时间和发动机转速，输出层为油门开度和汽车速度。PSO-Simulink算法与Simulink算法的结果对比如表1所示。从表1可知，模型采用PSOSimulink算法时，运算耗时0.41 s，迭代步数为499，而采用单纯Simulink算法时，运算耗时0.62 s，迭代步数为763。基于PSO-Simulink算法的汽车换挡操作模型运算过程中的PSO模拟优化结果适应度函数值的迭代如图3所示。从图3可知，模型在迭代19步时，适应度值为0.1，随着迭代步数的增加，适应度值趋近于0，在迭代步数为499时停止了运算。

表1 PSO-Simulink算法与Simulink算法结果对比

图3 PSO模拟优化结果适应度函数值的迭代

2.3 结果应用

发动机换挡模型三维关系如图4所示。从图4（a）可知，随着车速的增加，所需的油门开度略有增加，随着发动机转速的增加，对应的油门开度也逐渐增加；从图4（b）和图4（c）可知，在升挡和降挡过程中，随着油门开度的增加，车速逐渐增加，但升挡过程中，同挡位下车速增加较快。

图4 发动机换挡模型三维关系

发动机换挡（升挡或者降挡）过程中油门开度与车速关系曲线如图5所示。各种油门开度下的发动机车速与转速关系曲线如图6所示。从图5（a）可知，在升挡过程中，在油门开度为0～25%，1挡转化为2挡时，汽车速度为10 km/h；2挡转化为3挡时，汽车速度为75 km/h；3挡转化为4挡时，汽车速度为112 km/h。在油门开度为25%～90%时，所有挡位对应下的车速直线上升，然而在油门开度为90%～100%时，所有挡位对应下的车速均处于一个平台，1挡转化为2挡时，汽车速度为115 km/h；2挡转化为3挡时，汽车速度为140 km/h；3挡转化为4挡时，汽车速度为176 km/h。降挡过程的规律与升挡过程趋势基本一致。从图6知，在空挡时（油门开度为0），随着车速的增加，发动机转速基本无变化；油门开度分别为20%和40%时，随着车速的增加，发动机转速缓慢下降；油门开度分别为50%和100%时，随着车速的增加，发动机转速先略有升高，随后缓慢下降。

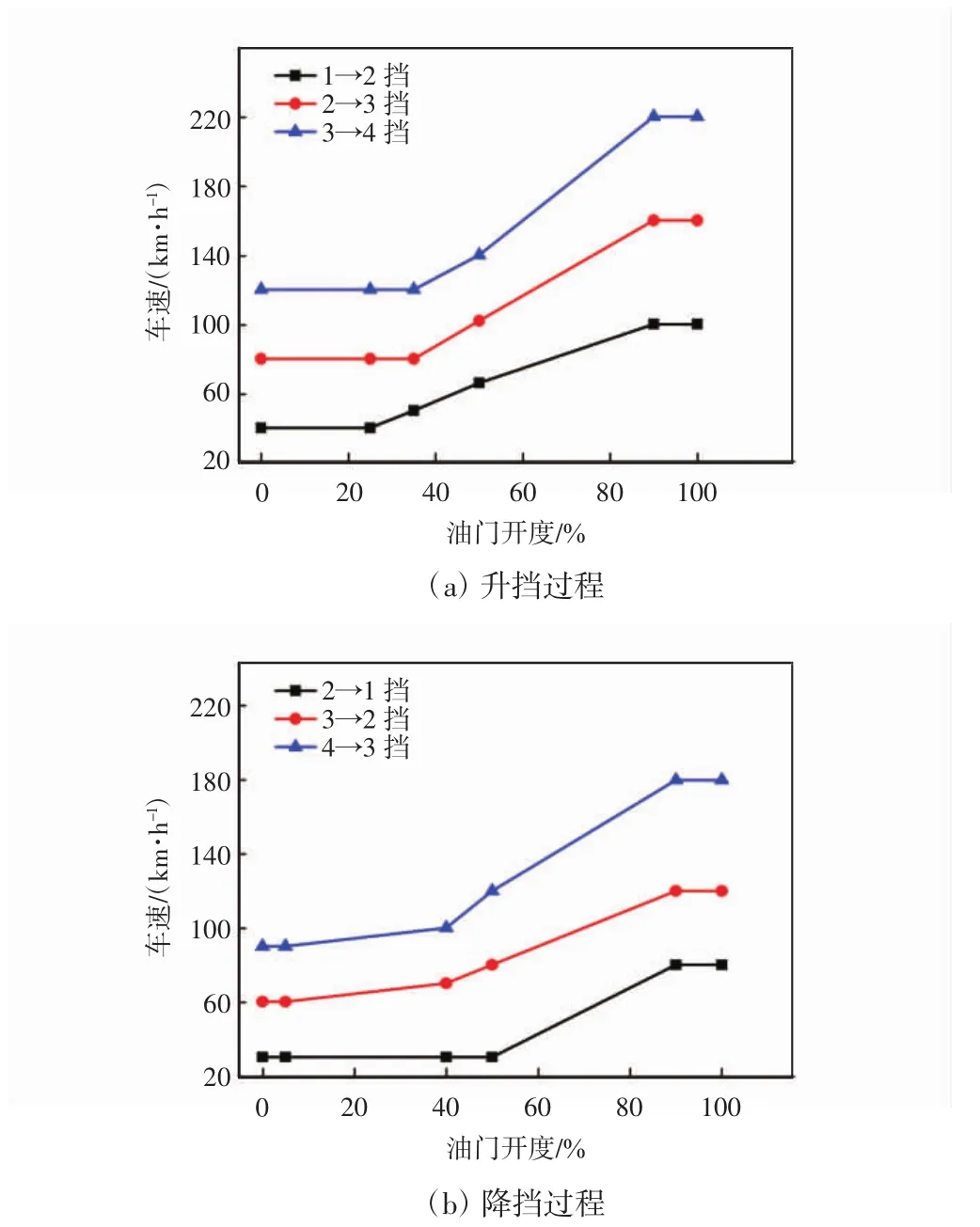
图5 发动机换挡过程中油门开度与车速关系曲线

图6 各种油门开度下的发动机车速与转速关系曲线

3 结语

本文基于PSO-Simulink算法建立了汽车自动变速器换挡模型，模型的输入层为换挡过程中的挡位、换挡时间和发动机转速，输出层为油门开度和车速。模型采用PSO-Simulink算法时，运算耗时0.41s，迭代步数为499，而采用单纯Simulink算法时，运算耗时0.62 s，迭代步数为763。结果表明：基于PSO-Simulink算法的汽车换挡操作模型可有效地节省时间。利用模型模拟的发动机换挡模型、发动机换挡（升挡或者降挡）过程中油门开度与车速关系及各种油门开度下的发动机车速与转速关系与实际结果一致。该模型可有效地指导实践生产，为优化工作提供一种新方法和新思路。