弧齿锥齿轮加工系统的几何仿真研究*

金映丽，程 远

(沈阳工业大学 机械工程学院，沈阳 110870)

0 引言

弧齿锥齿轮是一种传递相交轴或相错轴运动的传动元件[1]。加工系统的仿真是当前弧齿锥齿轮加工技术的一个重要方面,通过在虚拟环境中对弧齿锥齿轮加工机床进行调整，对弧齿锥齿轮进行加工来代替真实的调整、试切，不仅可以初步验证机床调整参数的合理性,还可以为接触分析(TCA)、加载接触分析(LTCA)等分析工作提供精确的齿面数据模型[2]。

国内外许多科研院校针对弧齿锥齿轮的加工进行了虚拟仿真的研究。梁伟开发出一套针对切齿加工过程仿真和数据分析软件[3]；王沉培等研究了准双曲面加工中计算机辅助设计的应用并开发出切齿仿真系统[4]；熊越东等根据弧齿锥齿轮数控加工特点，建立了具有真实感的加工仿真系统[5-7]； W P Wang等提出了一种刀具扫描体计算算法[8]。上述的学者利用相关的数控加工仿真软件或者利用三维建模软件的二次开发功能研发出的切齿仿真模拟系统,实现了弧齿锥齿轮加工的可视化，但是都没有进行考虑机床本身具有误差时加工系统的理论研究。

根据弧齿锥齿轮的切齿原理和啮合原理[9]推导出加工系统的数学模型，通过MATLAB中的SimMechanics模块创建弧齿锥齿轮加工系统的几何仿真模型，将数学模型与加工系统的几何仿真模型结合，获得弧齿锥齿轮的加工仿真齿面，该齿面与理论设计齿面相同，为研究含有误差的弧齿锥齿轮数控机床的几何仿真打下了基础。

1 加工系统几何仿真的数学模型

为了在几何仿真模型中能够正确控制各运动部件的运动，加工出与设计齿面一致的仿真齿面，需要建立加工系统的数学模型，获得弧齿锥齿轮几何仿真摇台与相关参数的数学关系，推导思路如下。

弧齿锥齿轮机床的加工系统由刀具、刀盘、摇台和工件4部分组成，以弧齿锥齿轮大轮为例建立的加工坐标系如图1所示，机床坐标系SO2=[Oo2,Xo2,Yo2,Zo2]、摇台坐标系Sg2=[Og2,Xg2,Yg2,Zg2]、刀盘坐标系St2=[Ot2,Xt2,Yt2,Zt2]、工件坐标系Sp2=[Op2,Xp2,Yp2,Zp2]、辅助坐标系Sa2=[Oa2,Xa2,Ya2,Za2]、辅助坐标系Sf2=[Of2,Xf2,Yf2,Zf2]，共6个坐标系。q2为角向刀位，S2为径向刀位，γ2为工件安装角，E2为垂直轮位,XB2为床位，X2为轴向轮位，φy2为摇台转角，rg2为工件转角，wg2为摇台转速，wp2为工件转速。

图1 弧齿锥齿轮大轮加工坐标系

在弧齿锥齿轮大轮机床坐标系中，啮合方程式为：

no2·vo2=0

(1)

式中，no2为刀盘切削锥面的法向矢量；vo2为啮合点处相对速度。

no2与vo2在机床坐标系So2中的方程为：

no2=no2(θ2,φg2)

(2)

vo2=vo2(g2)-vo2(p2)=
(wo2(g2)-wo2(p2))×ro2-Ro2×wo2(p2)

(3)

式中，θ2为刀具转角，u2为切削点到刀尖距离，ro2为刀盘上的点到其中心的矢量，表示为：

ro2=ro2(u2,θ2,φg2)

(4)

wo2(g2)为加工大轮时产形轮[10]在机床坐标系So2中的角速度，表示为：

(5)

wo2(p2)为加工大轮时工件在机床坐标系So2的角速度，表示为：

(6)

Ro2为So2的原点Oo2到Sp2的原点Op2的矢量，表示为：

(7)

由此推导得出f(φg,u,θ)=0，编程计算获得φg、u、θ三者之间的数学关系：

θ=f(φg,u)

(8)

根据弧齿锥齿轮设计齿面参数，计算加工时大轮摇台转角与切削点之间的关系，对建立的数学模型θ=f(φg,u)进行计算，获得当刀具转角θ固定不变时，不同摇台转角φg和刀具切削深度u之间的数学关系，利用该数学关系进行几何仿真可以获得齿面上的切削轨迹，三者之间的关系如图1所示。

图2 刀具切削深度和刀具转角的数学关系

2 加工系统的几何仿真模型

分析某5轴数控机床，保留底座、滑枕、刀具等关键结构，简化并去除端盖、密封圈、防护罩等次要结构，利用Solidworks建立数控机床的装配实体模型如图3所示。将该模型导入Simulink中，即可得到五轴数控机床的SimMechanics模型，系统将自动根据创建的三维模型的装配关系生成仿真模型的各个构件基本参数，获得各结构的基础模型。由于弧齿锥齿轮数控机床仿真模型中各模块之间具有高度的灵活性，可以通过插入控制函数或驱动副的方法实现加工系统的几何仿真。

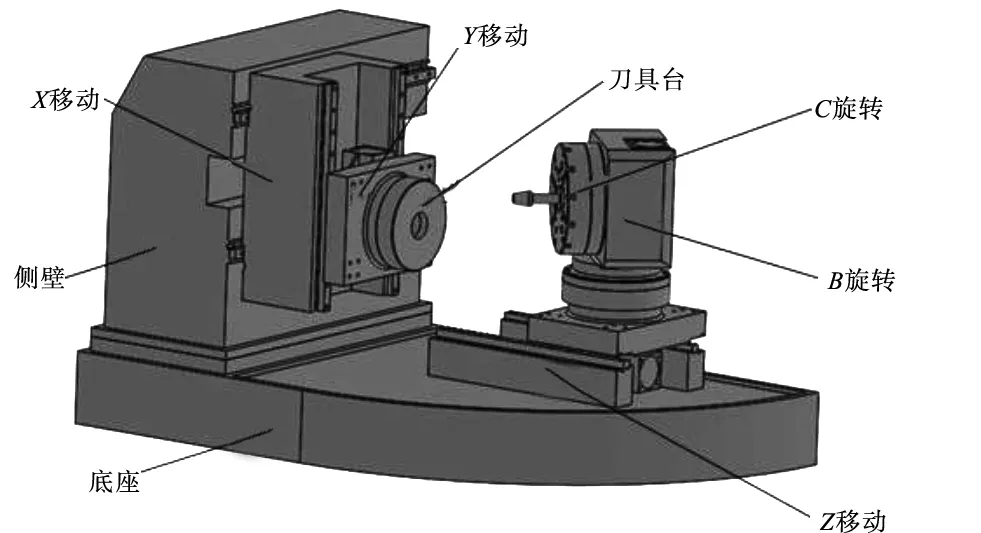
图3 弧齿锥齿轮数控机床三维模型

弧齿锥齿轮数控加工仿真模型分为三个部分，分别为基础仿真模型、控制模块、数据收集模块，建立并连接这三部分即可进行弧齿锥齿轮加工系统的几何仿真。

2.1 基础仿真模型的建立

数控机床通过5个数控轴来完成齿轮加工的全部运动，X、Y、Z为3个平动轴，B、C为2个转动轴。5个轴提供5个自由度，可以在加工过程中通过工件和刀盘的相对运动来实现齿轮加工的实际复杂展成运动。基础仿真模型具有三个平动轴以及两个旋转轴，以机床X平动轴和刀具主轴转动轴为例，仿真模块X轴通过‘Prismatic’模块连接到机床侧壁上，达到控制刀具沿X轴方向移动的目的，再将刀具仿真模块通过‘Revolute’模块连接到Y平动轴仿真模块上模拟刀具的旋转，最后通过上述方法将各个仿真模块连接完成基础仿真模型的建立。图3所示为加工系统的基础仿真模块。

图4 基础仿真模块

2.2 控制模块的建立

数控机床加工时通过X、Y、Z轴插补运动代替传统机床摇台机构，需要在X、Y、Z轴控制模块的Function程序中写入相应的运动规律函数，以保证X、Y轴可以模拟加工时摇台的运动情况，下面以X轴为例说明如何建立控制模块。

将机床X平动轴数学模型y=s·sin(θ+q)与加工系统数学模型θ=f(φg,u)结合，其中s为径向刀位，θ为刀具转角，q为角向刀位，在Simulink中构建驱动模块，通过Function程序建立X轴运动函数，并与Clock函数连接，以时间t作为X平动轴运动的自变量来控制X轴的运动。在控制X平动轴位移的同时，与速度、加速度联合MUX模块，输入到Joint Actuator中实现对X平动轴的控制。

如图4所示为X轴控制模块。

图5 X轴控制模块

2.3 数据收集模块的建立

数据收集模块如图5所示连接Body Sensor与To Workspace，将仿真加工的运动轨迹通过Body Sensor模块进行输出，并利用To Workspace模块将输出的仿真加工运动轨迹三维坐标点保存到MATLAB的数据变量区，方便后续在MATLAB当中的进行数据处理工作。

图6 数据收集模块

3 加工系统几何仿真分析

在仿真过程中将数学模型导入仿真模型的控制模块中，通过仿真得到轮齿齿面的加工坐标点。某型弧齿锥齿轮齿坯参数和加工调整参数见表1和表2。

表1 弧齿锥齿轮齿坯参数

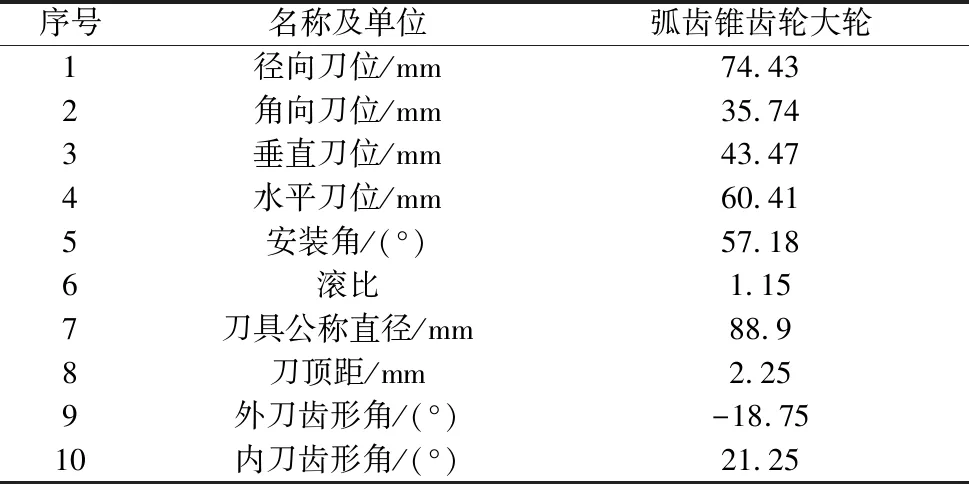
表2 加工机床调整参数

根据数学模型中的摇台角，编写X，Y轴控制器中的 Function 函数，同时在模块Revolute 中输入相对应的刀具转角，模拟加工系统在某一摇台转角(170°～205°)时对应不同的刀具转角与刀具切削深度(0～15mm)。对弧齿锥齿轮加工系统进行几何仿真，即可得出刀盘在加工过程中与弧齿锥齿轮实际齿面接触的三维坐标，其中刀盘与凹面所接触点的坐标如表3 所示。

表3 加工时刀盘与凹面所接触点的坐标

分析刀具在仿真加工过程中与实际齿面所接触的数据点，将这些数据点经过MATLAB编程计算得出大齿轮凹面坐标点，根据坐标点数据在三维软件进行绘制。构建Nurbs三次样条曲面，通过旋转坐标系使之与理论曲面重合，并分析比较弧齿锥齿轮的仿真齿面与理论设计齿面，两者的重合精度可以达到10-3。图6所示为几何仿真过程中刀具在齿坯上的加工轨迹。

图7 弧齿锥齿轮凹面仿真齿面

4 结论

根据机床加工理论与齿轮啮合原理，通过弧齿锥齿轮加工时产形轮与齿坯的相对速度的和法矢量建立了加工系统的数学模型，通过数学模型中摇台转角、刀具转角、刀具切削深度三者之间的关系对弧齿锥齿轮加工系统几何仿真加以控制，获得了仿真加工系统的仿真加工齿面，该加工齿面与理论设计齿面相同。在该五轴数控机床加工系统几何仿真中加入误差模块，可以研究不同误差(包括机床本身误差)对仿真加工齿面的影响，为具有误差的几何仿真分析奠定了基础。