履带式设备接地比压的分析
2019-04-08焦宏章
焦宏章
(中国煤炭科工集团太原研究院有限公司,太原 030006)
履带行走机构被广泛应用于矿山机械和工程机械。主要由导向轮、涨紧装置、支重轮、拖链轮、驱动装置、履带和履带架组成。具有承载大,爬坡能力强,地面适应性好等诸多突出特点。其中履带接地比压是设备的重要参数之一,目前在矿山机械仅标称平均接地比压,即机重与履带接地面积的比值,由于计算过程中没有考虑重心的影响,因此平均接地比压不能反映地基的真实受压情况,设备实际工作过程中的真实接地比压比平均比压大很多,甚至数倍于平均比压,因此履带行走机构设计过程中平均接地比压会留有足够的安全系数,防止地面被压溃,引发事故[1-2]。即使对接地比压限制较高的工程起重设备,目前检索到的关于接地比压的计算文献,也是在各种简化的基础上的进行计算,与真实接地比压误差较大[3-7]。针对这一问题,本文建立了履带式设备工作过程的等效模型,假设履带接地面积内比压呈平面分布,推导了各种工况下最大接地比压的计算公式。
1 建立履带式设备的等效模型
履带式设备工作过程中的受力模型如图1所示,由重力G0和执行机构受到的反作用力(FX,FY,FZ,MX,MY,MZ)组成,重心位于(X0,Y0,Z0),反作用力作用点位于(X1,Y1,Z1)为了便于分析,将此受力模型等效为设备只受重力G,重心位置为(X,Y,Z).建立图1所示坐标系,坐标原点取在接地比压最大点处,Y向取履带行走方向,X向取设备宽度方向。
根据等效前后Z向支反力不变,可列
G=G0+FZ
(1)
根据等效前后X向倾覆力矩不变,可列
G×Y=G0×Y0+FY×Z1+FZ×Y1+MX
(2)
根据等效前后Y向倾覆力矩不变,可列
G×X=G0×X0+FX×Z1+FZ×X1+MY
(3)
联合式(1)~(3)可求得等效后的设备模型参数:G,X,Y.

图1 履带式设备工作过程中的受力模型
Fig.1 Force model in the working process of caterpillar equipment
2 履带接地比压计算
根据上节计算得出的G,X,Y.可进一步计算履带接地比压。现有文献只有重心在X向对称面上接地比压的计算方法,本文根据重心是否在行走部的对称面上,分三种工况进行分析,涵盖重心在任意位置下的最大接地比压计算方法。
2.1 重心在行走部X向对称面上
若重心在行走部X向对称面上,建立图2所示坐标系,使重心坐标X=(B+b)/2,同时Y≤L/2,假设履带接地比压呈平面分布,则可列式(4)所示比压在接地范围内的分布方程:
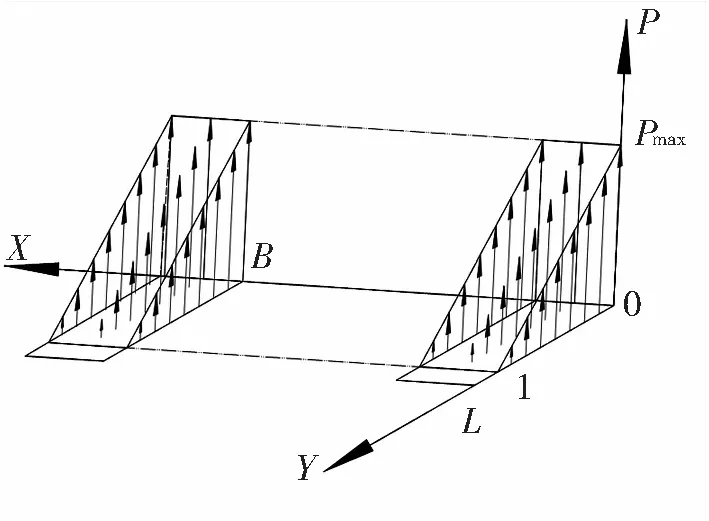
图2 履带接地比压分布图-X
Fig.2 The distribution of ground pressure-X
图2中:L——履带接地长度,l——履带接地比压分布平面与Y轴交点坐标,b——履带板宽度,B——履带中心距,Pmax——履带最大接地比压。
(4)
根据Z向受力平衡,可列式:
(5)
根据X向力矩平衡,可列式
(6)
联合式(5)和式(6)可得:
(7)
l=3Y
(8)
式(5)和式(6)的积分区间为(0,l),适合履带接地比压分布平面与Y轴交点坐标l≤L的工况,根据式(8)要求Y≤L/3.若L/3
(9)
综上,若Y≤L/3,根据式(7)计算最大接地比压;若L/3 设备工作过程中一般要求履带接地面积内任意点处的比压0,即等效后的设备重心L/3 若重心在行走部Y向对称面上,建立图3所示坐标系,使重心坐标Y=L/2,同时X≤(B+b)/2,假设履带接地比压呈平面分布,则可列式(10)所示比压在接地范围内的分布方程: (10) 图3 履带接地比压分布图-Y 图3中:L——履带接地长度,m——履带接地比压分布平面与X轴交点坐标,b——履带板宽度,B——履带中心距,Pmax——履带最大接地比压。 根据Z向受力平衡,可列式: (11) 根据Y向力矩平衡,可列式 (12) 联合式(11)和式(12)可得: (13) (14) 由于计算前不知道履带接地比压平面与X轴交点位置,因此式(11)和(12)中的左半侧履带的积分区间初定为(B,B+b),然后求解得出最大接地比压Pmax和履带接地比压平面与X轴交点坐标m,若m 图4 含有负值接地比压的分布图-Y 根据履带接地比压分布平面与X轴交点坐标,分三个区间进行讨论: (1)m≥B+b 若m≥B+b,代入式(14)可得: 说明履带在接地面积范围内最小接地比压大于0,则最大接地比压按式(13)计算。 (2)B 若B 说明左侧履带有一部分接地面积的接地比压等于0,计算过程中左侧履带的X向积分区间为(B,m),将式(11)和式(12)修改后重新积分计算求的Pmax.所有式子全部用符号替代,解析式非常庞大,由于篇幅限制文中暂且省略,应用数学软件MATLAB照文章所述列示可以非常容易地计算出最大接地比压Pmax. (3)b 若b 说明履带严重偏载,左侧履带的接地比压全部等于0,将式(11)和式(12)中的左侧删除后重新积分计算求的Pmax. 设备工作过程中一般要求履带接地面积内任意点处的接地比压大于0,即 若重心偏离行走部对称面,建立图5所示坐标系,使重心坐标X≤(B+b)/2,同时Y≤L/2,假设履带接地比压呈平面分布,则可列式(15)所示比压在接地范围内的分布方程: (15) 图5 履带接地比压分布图 图5中:L——履带接地长度,l——履带接地比压分布平面与Y轴交点坐标,b——-履带板宽度,k——履带接地比压分布平面与XY平面交线的斜率,B——履带中心距,Pmax——履带最大接地比压。 根据Z向受力平衡,可列式: (16) 根据X向力矩平衡,可列式: (17) 根据Y向力矩平衡,可列式: (18) 联合式(16)~(18)求解可得: (19) (20) (21) 由于计算前不知道比压平面与XY平面交线位置,因此式(16)~(18)的Y向积分区间初定为(0,L),求解得出最大接地比压Pmax,以及比压平面与Y轴交点坐标l,比压平面与XY平面交线的斜率k,代入式(15)得出比压平面方程P(x,y). 若计算得出的履带接地比压分布平面与XY平面交线切入履带接地面积,按(16)-(18)式计算会导致部分接地面积的比压是负值(图6所示),一旦出现这样的情况,履带的实际接地比压会重新分布,因此需要对式(19)-(21)的计算结果进行进一步讨论。 图6 含有负值接地比压的分布图 根据左侧履带比压最小点(B+b,L)和右侧履带比压最小点(b,L)两点的比压值,分三个组合进行讨论: P(B+b,L)≥0 若P(B+b,L)≥0,说明比压平面与XY平面交线未切入履带接地面积,履带在接地面积范围内最小接地比压大于0,则最大接地比压按式(19)计算。 P(B+b,L)<0,且P(b,L)≥0 若P(B+b,L)<0,说明履带接地比压分布平面与XY平面交线已经切入履带接地面积,履带的实际接地比压会重新分布,计算过程中左侧履带的Y向积分上限为l+kx,右半侧履带的积分上限为L,将式(16)~(18)修改后重新积分求得Pmax. P(B+b,L)<0,且P(b,L)<0 若P(B+b,L)<0,且P(b,L)<0,说明履带偏载非常严重,接地比压分布平面已经深度切入履带接地面积,计算过程中左侧履带和右侧履带的Y向积分上限全部为l+kx,将式(16)~(18)修改后重新积分计算得出Pmax. 设备工作过程中一般要求履带接地面积内任意点处的接地比压大于0,即P(B+b,L)≥0. 以某型号履带式巷道修复机为例进行验算。具体参数如下:设备总重G=350 000 N,履带接地长度L=2 000 mm,履带板宽b=500 mm,履带中心距B=2 000 mm,按照图1建立计算坐标系。假设设备重心在不同位置,应用前文所述计算公式可计算得出表1所示计算结果。 表1 不同重心对应的接地比压 工况重心(mm)实际比压(MPa)实际比压/平均比压X-Y1250,10000.1751X1250,5000.4672.67Y900,10000.251.43X-Y900,9000.30251.73 分析表中数据可以得出以下结论: (1)若设备重心位于行走部接地形心,应用本文所推导的公式计算得出的接地比压与平均接地比压相等。 (2)若设备重心位于行走部X向对称面,应用本文所推导的公式计算得出的接地比压与参考文献1、2计算的得出的接地比压相等,验证了公式的正确定。 (3)若设备重心偏离行走部接地形心,实际最大接地比压远大于平均接地比压,即平均接地比压不足与反映地基的真实受压情况。 (4)若设备重心位于行走部Y向对称面或者偏离行走部对称面,本文首次给出了最大接地比压的计算解析式。 本文建立了履带式设备工作过程的等效模型,基于履带接地面积内比压呈平面分布的假设,系统推导了各种工况下最大接地比压的计算公式,得出如下结论: (1)等效后设备重心在行走部X向对称面上,若Y向坐标Y≤L/3,根据式(7)计算最大接地比压Pmax;若L/3 (4)若等效后设备重心不在行走部的对称面上,根据式(19)~(21)初算最大接地比压Pmax和接地比压分布平面方程P(x,y),然后根据左右两侧履带距离坐标原点最远处两点的比压值P(B+b,L)和P(b,L),进一步讨论分析得出最大接地比压。设备设计过程中一般要求距离坐标原点最远处的比压大于等于0,即P(B+b,L)≥0. (5)对于重心在X向对称面上本文所推导公式的计算结果与参考文献计算结果相等。对于设备重心偏离行走部接地形心,其实际最大接地比压会远大于平均接地比压,具体数值可依据本文所述公式进行计算。2.2 重心在行走部Y向对称面上
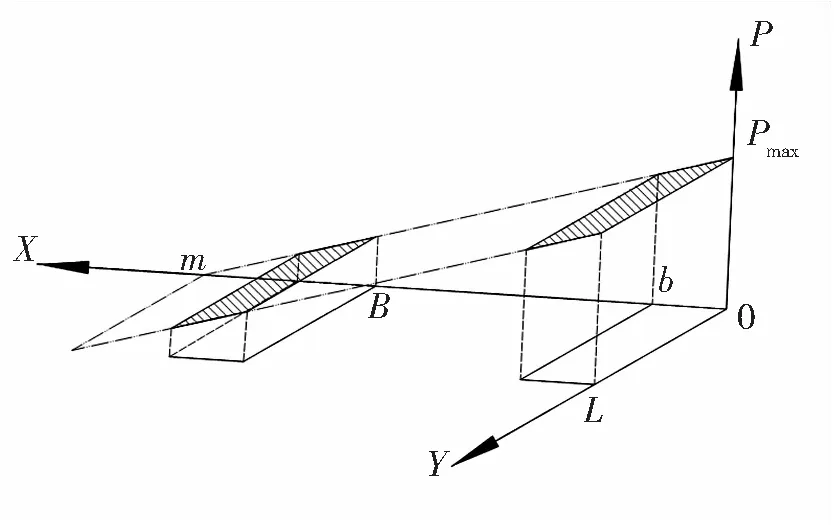
Fig.3 The distribution of ground pressure-Y
Fig.4 The distribution of contain negative ground pressure-Y

2.3 重心偏离行走部对称面
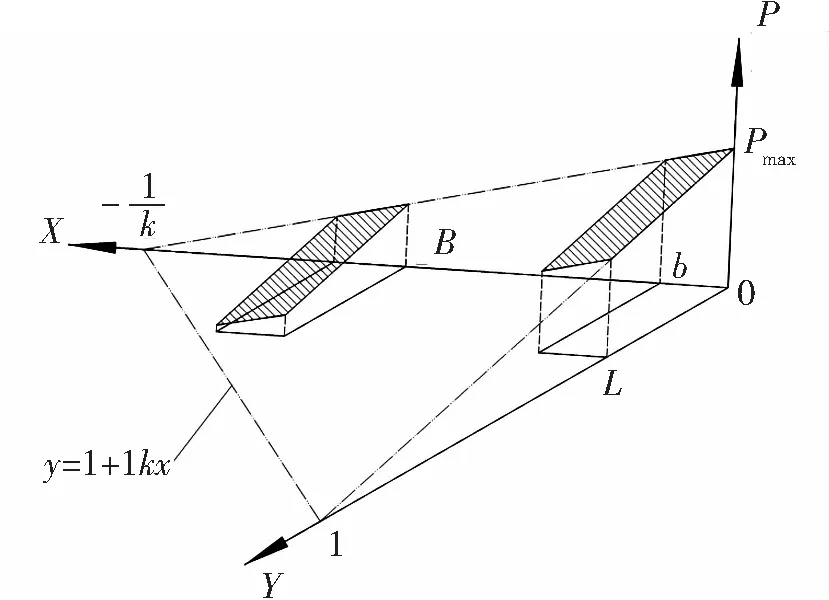
Fig.5 The distribution of ground pressure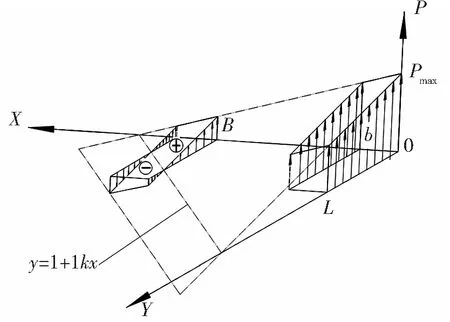
Fig.6 The distribution of ground pressure containing negative values3 应用实例
Tab.1 The ground pressure under different centers of gravity position
4 结 论

