基于惯性权重的蝙蝠算法

杨晓琴

(太原广播电视大学，太原 030024)

随着近年来社会快速发展，在许多工程应用中出现大量单目标优化问题，如求解光伏发电系统中的全局最大功率点问题[1]、柔性车间调度问题[2]以及梯级水电站中长期经济调度问题等[3-6]。这些问题大部分具有非连续、不可导和不可微等特征，利用经典的数学方法一般无法有效求解此类问题。针对此类问题，许多研究者受到自然界生物信息的启发，相继提出了蝙蝠算法(Bat Algorithm, BA)[7]，微粒群算法(Particle Swarm Optimization Algorithm, PSO)[8]和布谷鸟搜索算法(Cuckoo Search algorithm, CS)[9]等。由于此类启发式算法对求解问题的约束条件较少，而且可以有效地解决实际应用中的复杂优化问题，迅速得到许多研究者的追捧和深入研究。

蝙蝠算法，作为一种有效地求解复杂优化问题的启发式算法，虽然被广泛应用于实际问题，但仍存在求解精度较低、算法后期移动步长较小、局部搜索能力较差以及容易陷入局部最优的缺点。为解决算法后期移动步长较小的问题，张宇楠提出蝙蝠个体随着迭代次数的增加，步长自适应调整的策略；Bahman[10]则针对蝙蝠个体提出了四种更新方式，并根据每种更新方式的特点分配不同权重，有效改进了算法的求解性能。针对算法局部搜索能力差的缺陷，Cai[11]提出利用高斯分布代替均匀分布，有效地改进了算法的局部搜索能力；刘长平[12]利用混沌序列的随机性和遍历性，提出了基于混沌搜索策略的蝙蝠优化算法。为解决蝙蝠算法容易陷入局部最优的问题，杨晓琴[13]提出将Levy飞行引入蝙蝠速度更新公式，提出了融合Levy飞行的蝙蝠算法；同样针对此问题，孙健[14]提出利用混沌变异的方式改进算法性能；同样，郭旭[15]提出蝙蝠个体不再单一地向全局最优蝙蝠学习,而是与邻域内所有蝙蝠进行信息共享与交流,并根据自身寻优能力自适应地调节向其他蝙蝠学习的力度；上述几种方式有效地改进了蝙蝠算法跳出局部最优的能力。为将蝙蝠算法应用于离散化的优化问题，李枝勇[16]将遗传算法中的变异思想融入蝙蝠算法，并引入诱变因子进一步提升算法的求解精度。

为了进一步提升蝙蝠算法求解精度，改进蝙蝠算法过早收敛的缺陷，本文详细分析了缺陷产生了的原因，并针对性地提出基于惯性权重的蝙蝠算法。在实验部分，本文详细分析了惯性权重采用不同分布函数时算法的性能，并与其他算法做了详细比较，验证了本文所提算法的有效性。

1 标准蝙蝠算法

蝙蝠是唯一一种具有翅膀的哺乳类动物，其在夜间视线较差的情况下，利用其回声定位能力能够轻易且有效地地捕捉食物和躲避障碍物。受蝙蝠此种行为的启发，Yang提出了模拟蝙蝠回声定位行为的蝙蝠算法(Bat algorithm, BA).为简化BA模型，Yang提出了三条假设：

(1)食物与障碍物之间的差异依靠蝙蝠的回声定位判断；

(2)在位置Xi处，以速度Vi飞行的蝙蝠个体，通过波长(频率fi)和脉冲(响度Ai)搜索猎物；而且，蝙蝠个体可以根据与搜索目标的接近程度自适应调整波长。

(3)脉冲随着不同情境变化也不同，本文假设脉冲随着代数增加而减少，即在Amax到Amin之间变化。

根据上述条件，可定义蝙蝠个体i在t+1时刻位置和速度全局更新方式，如下：

(1)

(2)

fi=fmin+(fmax-fmin)×β

(3)

式中，β∈[0,1]，fmax和fmin分别是脉冲频率上限和下限。

局部搜索方式可定义如下：

(4)

为模拟蝙蝠个体在搜索前期以较大脉冲强度搜索目标，后期发现猎物后逐渐减少脉冲频率的过程，本文采用以下方式描述此过程：

(5)

(6)

标准蝙蝠算法伪代码如下所示：

算法1：标准蝙蝠算法

Begin

初始化蝙蝠个体位置，速度以及其它基本参数；

While (未满足结束条件)

用式(3)更新蝙蝠个体频率；

用式(1)更新蝙蝠个体速度；

用式(2)更新蝙蝠个体位置；

用式(4)更新蝙蝠个体位置；

End

计算每个蝙蝠个体适应值；

End

选择当前最优个体;

End

输出最优个体;

End

2 基于惯性权重的蝙蝠算法

(7)

式中w为随机数。本文采用常见的三种随机数生成方式，即r=randn为服从标准高斯分布的随机数(即期望为0，方差为1)、r=rand在[0,1]区间变化的随机数, 以及r=λe-λx(在实验部分用exp表示)为服从指数分布的随机数，其中指数分布对应率参数λ设置为1.0，x=1-Gcurrent/Gmax,Gcurrent为当前代数，Gmax为算法最大代数。上述三种方式将在后续实验中详细验证其性能, 本文所提算法命名为基于惯性权重的蝙蝠算法(Bat Algorithm with Inertia Weight, IWBA).

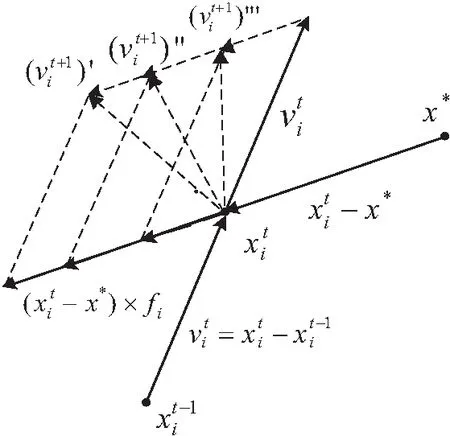
图1 标准蝙蝠算法速度更新示意图
Fig.1 Illustration of velocity update in BA

图2 改进速度更新示意图
Fig.2 Illustration of improved velocity update

基于惯性权重的蝙蝠算法伪代码如下所示：

算法2：基于惯性权重的蝙蝠算法

Begin

初始化蝙蝠个体位置，速度以及其它基本参数；

While (未满足结束条件)

用式(3)更新蝙蝠个体频率；

用式(7)更新蝙蝠个体速度；

用式(2)更新蝙蝠个体位置；

用式(4)更新蝙蝠个体位置；

End

计算每个蝙蝠个体适应值；

End

选择当前最优个体;

End

输出最优个体;

End

3 仿真分析

为验证本文所提算法性能，本文采用微粒群算法(Particle Swarm Optimization algorithm, PSO)和标准BA作为对比算法，其中每个算法相应参数按照开发者建议设置。测试函数采用CEC2013测试集[17-18]，如表1所示，括5个单峰函数、15个多峰函数以及8个复合函数。种群数量设置为100，每个算法独立运行51次，个体维度为30维，算法最大运行代数为3 000次。算法评价指标为平均值误差(Mean Error)：

(8)

式中f*为理论最优适应值，fbest为算法所求最优适应值。

3.1 惯性权重w所采用不同分布策略讨论

表2所示为惯性权重w采用不同分布策略时对应IWBA算法的求解结果，其中最优结果用黑体显示, 最后一行“w/l/t”表示惯性权重采用均匀分布或者指数分布的算法与采用高斯分布的算法相比分别在w个函数上较优，在l个函数上较差以及在t个函数上相等。从最后一行统计结果可以看出，惯性权重w采用高斯分布时对应算法比采用均匀分布和指数分布对应的算法性能较优。

表1 CEC2013测试函数
Tab.1 CEC2013 test suit

函数函数名称最优值(无单位)F1Sphere Function-1 400F2Rotated High Conditioned Elliptic Function-1 300F3Rotated Bent Cigar Function-1 200F4Rotated Discus Function-1 100F5Different Powers Function-1 000F6Rotated Rosenbrock’s Function-900F7Rotated Schaffers F7 Function-800F8Rotated Ackley’s Function-700F9Rotated Weierstrass Function-600F10Rotated Griewank’s Function-500F11Rastrigin’s Function-400F12Rotated Rastrigin’s Function-300F13Non-Continuous Rotated Rastrigin’s Function-200F14Schwefel's Function-100F15Rotated Schwefel's Function100F16Rotated Katsuura Function200F17Lunacek bi-Rastrigin Function300F18Rotated Lunacek bi-Rastrigin Function400F19Expanded Griewank’s plus Rosenbrock’s Function500F20Expanded Scaffer’s F6 Function600F21Composition Function 1700F22Composition Function 2 800F23Composition Function 3 900F24Composition Function 4 1 000F25Composition Function 5 1 100F26Composition Function 6 1 200F27Composition Function 7 1 300F28Composition Function 8 1 400搜索空间[-100,100]D

表2 不同分布策略对应算法实验结果对比
Tab.2 Comparison of IWBA with different distribution strategies

函数IWBAw=randn(无单位)w=rand(无单位)w=exp(无单位)〛F15.00E-011.95E+002.04E+00F25.39E+052.70E+063.52E+06F34.63E+072.22E+083.13E+08F42.80E+023.60E+042.16E+04F52.94E-015.55E-015.73E-01F65.29E+014.67E+016.22E+01F71.49E+022.61E+021.78E+02F82.09E+012.09E+012.09E+01F93.56E+013.38E+013.42E+01F101.24E+001.31E+001.32E+00F114.53E+024.60E+024.18E+02F124.55E+024.54E+023.66E+02F133.94E+024.83E+024.31E+02F144.70E+034.85E+035.09E+03F154.63E+034.80E+034.56E+03F169.96E-012.08E+002.31E+00F173.88E+024.65E+027.61E+02F183.78E+024.25E+027.99E+02F192.68E+013.04E+015.79E+01F201.45E+011.47E+011.44E+01F212.49E+023.40E+023.67E+02F225.52E+036.00E+035.97E+03F235.60E+036.14E+035.82E+03F243.20E+023.22E+023.13E+02F253.50E+023.60E+023.37E+02F262.28E+022.97E+022.00E+02F271.36E+031.34E+031.27E+03F283.35E+034.17E+032.87E+03w/l/t4/24/09/19/0

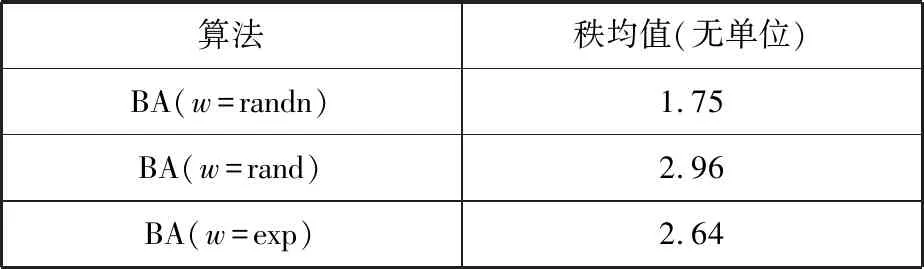
表3为上述采用不同分布策略的算法Friedman测试结果。从表3测试结果可以看出，惯性权重w采用高斯分布时对应算法具有较小的秩均值，即惯性权重采用标准高斯分布时对应算法具有较优性能。

表3 Friedman测试结果
Tab.3 Friedman test results

算法秩均值(无单位)BA(w=randn)1.75BA(w=rand)2.96BA(w=exp)2.64

3.2 不同算法性能对比

为进一步测试本文所提算法性能，本部分将IWBA(惯性权重w采用高斯分布)与PSO, 混沌BA以及标准BA做进一步对比。表4列出了多个对比算法实验结果。从表4最有一行对比结果可以看出，IWBA相比于标准BA以及PSO具有较大的优势。在F23-F27测试函数上，IWBA结果略差于标准BA, 其原因是本文所设计的改进机制旨在使算法跳出局部最优，使得对部分局部最优或者全局最优无法充分地搜索，这也从侧面说明了本文所提算法在跳出局部最优方面的有效性。

表4 不同算法对比
Tab.4 Comparison of different algorithms

函数IWBA(无单位)BA(无单位)PSO(无单位)F15.00E-011.83E+002.96E+04F25.39E+053.26E+064.02E+08F34.63E+072.26E+081.65E+14F42.80E+023.44E+045.25E+04F52.94E-014.74E-011.04E+04F65.29E+015.99E+014.54E+03F71.49E+021.75E+021.60E+04F82.10E+012.10E+012.10E+01F93.56E+013.57E+014.05E+01F101.24E+001.32E+003.98E+03F114.53E+023.81E+025.72E+02F124.55E+024.04E+025.18E+02F133.94E+024.73E+025.43E+02F144.70E+034.61E+038.21E+03F154.63E+035.17E+037.19E+03F169.96E-012.30E+002.59E+00F173.88E+029.31E+027.25E+02F183.78E+029.49E+027.12E+02F192.68E+016.15E+019.52E+04F201.45E+011.46E+011.50E+01F212.49E+023.70E+022.28E+03F225.52E+035.66E+038.55E+03F235.60E+035.73E+038.38E+03F243.20E+023.12E+023.76E+02F253.50E+023.43E+023.92E+02F262.28E+022.00E+022.44E+02F271.36E+031.26E+031.49E+03F283.35E+033.79E+034.43E+03w/l/t8/20/00/28/0

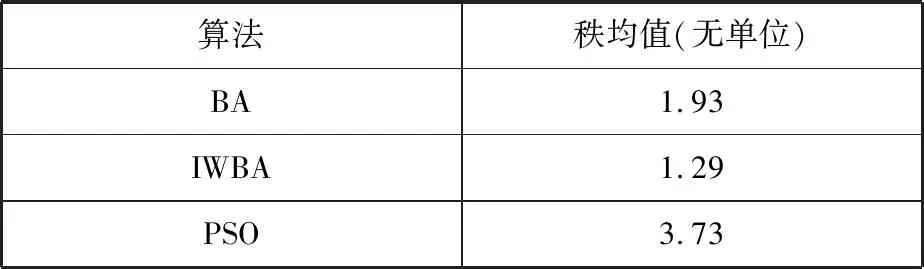
表5列出了不同算法 Friedman检验结果，从对比数据可以看出本文所提算法具有最小秩均值。综合以上实验结果可以得出，本文所提改进算法有效地改进了个体陷入局部最优的难题，提升了算法搜索性能。

表5 不同对比算法Friedman测试结果
Tab.5 Friedman test results of different comparison algorithms

算法秩均值(无单位)BA1.93IWBA1.29PSO3.73

4 结论

在对蝙蝠算法速度更新方式详细分析的基础上，本文发现标准蝙蝠算法原有速度更新方式有利于发掘当前全局最优解附近个体；然而，当个体陷入局部最优时，此时全局速度更新方式无法有效地跳出局部最优解。针对此缺陷，本文提出了基于惯性权重的蝙蝠算法，即对速度添加惯性权重。实验结果显示，本文所提IWBA有效地提高了蝙蝠算法的性能。