基于相干度优化的极化顺轨干涉SAR慢小目标CFAR检测

张鹏， 张嘉峰， 刘涛，*

(1. 海军工程大学电子工程学院, 武汉 430033； 2. 海军作战支援舰第二支队， 舟山 316000)

地面运动目标检测(Ground Moving Target Indication,GMTI)是合成孔径雷达(Synthetic Aperture Radar,SAR)遥感领域重要的研究分支[1]。近年来，随着SAR顺轨干涉(Along-Track Interferometry,ATI) 理论的逐步完善，基于干涉图的GMTI方法因其具有对慢速运动目标的检测能力而备受关注[2-4]。但现有的、包括干涉图在内的SAR GMTI方法在对慢速运动目标尤其是淹没在背景杂波内的慢动小目标进行检测时，仍存在虚警概率与漏检概率高的问题，且最小可检测速度往往高于预期的结果。在经典雷达极化中，全极化雷达已被证明能够检测单极化雷达所检测不到的弱小目标[5-6]，因而利用全极化信息进行GMTI或许是解决上述问题的有效手段[7-10]。

利用全极化SAR(Polarimetric SAR,POLSAR)进行GMTI的研究分为单通道与多通道2类方法。在单通道POLSAR GMTI领域，加拿大学者Liu[11-12]提出利用当前分时极化测量体制POLSAR所获取的交叉极化项进行干涉处理以提高运动目标检测性能的方法，并采用CV-580 SAR实测全极化数据证明了交叉极化进行GMTI的潜力，但本质上这种利用了HV与VH极化的互易性的方法仍可看作单极化ATI方法的拓展。对于多通道POLSAR GMTI，文献[13]指出利用单航过极化干涉SAR进行GMTI是未来极化干涉技术的重要应用，并以可测速区间为优化准则对全极化顺轨干涉SAR(AT-POLINSAR，添加前缀“AT-”用以区分极化交轨干涉SAR(POLINSAR))系统进行了优化设计，但该研究立足于现有的分时极化测量SAR，并不适用于未来同时极化测量体制且没有对新系统进行具体的检测器设计。文献[7-10]指出具有精确极化散射特性测量能力的同时极化测量技术是未来乃至相当长一段时期内极化测量体制发展的主流趋势，因而开展同时测量AT-POLINSAR慢动目标自动检测算法的研究对POLSAR GMTI理论体系的建立以及AT-POLINSAR系统设计都具有重要的意义。当前可直接用于AT-POLINSAR进行GMTI的算法主要有2类：一是文献[1]提出的基于多频段多孔径极化SAR(MFMA POLSAR)的方法，即通过最优极化干涉理论[14-16]对MFMA POLSAR回波降维后采用杂波对消进行运动目标成像；二是文献[17]提出的利用对数似然比(Likelihood-Ratio Test,LRT)[18]对目标极化干涉协方差矩阵进行检测的方法。但这2种方法都难以推导检测量的统计分布，且依赖于对目标先验信息的获取，不宜扩展成恒虚警(Constant False Alarm Rate,CFAR)检测器。综上所述，为设计实用的AT-POLINSAR慢动目标自动检测算法，主要有2方面亟待研究的问题：一是建立POLSAR 顺轨干涉的统计建模与参数估计理论，与传统单极化ATI不同的是，全极化ATI除考虑同一极化通道内的干涉相干度外，还要额外考虑不同极化通道之间的相干度以充分挖掘运动目标与杂波背景之间的差异；二是构造性能较优且解析门限易于求解的检测量，单极化条件下利用干涉图幅度和相位联合CFAR检测量的检测性能较优[2-4]，那么如何将这种方法扩展至全极化或者针对极化矢量干涉回波重新构造新的检测量将是实现慢动目标CFAR检测的关键。

针对上述问题，本文首先对单基线AT-POL-INSAR回波进行建模分析；然后针对其6维极化矢量干涉数据，提出基于背景杂波平均相干度最优的降维新方法，从高维干涉矢量中合成出次优极化标量干涉数据，从而可以将单极化顺轨干涉SAR(AT-INSAR)慢动目标检测算法直接应用到全极化系统进行目标检测；最后，分别采用蒙特卡罗仿真实验与场景检测实验对次优极化、单极化的慢动目标CFAR检测进行性能对比。

1 全极化顺轨干涉SAR系统

本节基于MFMA POLSAR[1]与分时极化AT-INSAR[13]的设计思路，提出一种设备复杂度相对较低、可实现度高的单基线AT-POLINSAR的新系统。基于对系统工作方式、天线收发模式与信号形式的设计，建立了极化矢量干涉模型, 将SAR单极化顺轨干涉扩展成全极化矢量干涉。本节的AT-POLINSAR的信号模型可扩展到MFMA POLINSAR，同时，矢量干涉模型也适用于分时极化测量顺轨干涉SAR。

1.1 AT-POLINSAR系统信号与回波建模

图1为单基线AT-POLINSAR系统的成像几何示意图，设雷达平台在高度为H的直线轨迹以速度vp匀速飞行，沿雷达平台运动方向配置2副相同的全极化天线分别作为前、后向干涉通道m和s，并在不同的方位采样时刻同时发射h极化与v极化状态的正交波形，从而在h、v极化天线之间形成了共同的物理干涉基线2Lb。关于天线工作方式，本文假设2副天线按照“乒乓”模式工作，即2副天线轮流发射全极化信号并同时接收极化回波，相较于全孔径发射子孔径接收的方案，这种方式在基线配置、系统实现等方面具有更高的灵活性[19]。

图1中，β为合成孔径雷达下视角，Ra为雷达成像斜距，θ为斜视角，Lb为基线长度，vp为平台运动速度，设雷达平台运动方向(方位向)为x轴正方向，设地距方向为y轴正方向。在t=0时刻，前向干涉通道m的天线相位中心的坐标为(0,0,H)，后向干涉通道s的天线相位中心的坐标为(-Lb,0,H)，设目标以初始坐标T0(x0,y0,0)作匀速直线运动，其方位向与距离向的速度分量分别为vx、vy。m通道天线发射全极化线性调频(Linear Frequency Modulation,LFM)信号s=[sh(τ),sv(τ)]T[9-10]，sh(τ)与sv(τ)分别为水平、垂直极化，两者相互正交，且具有如下的共同形式：

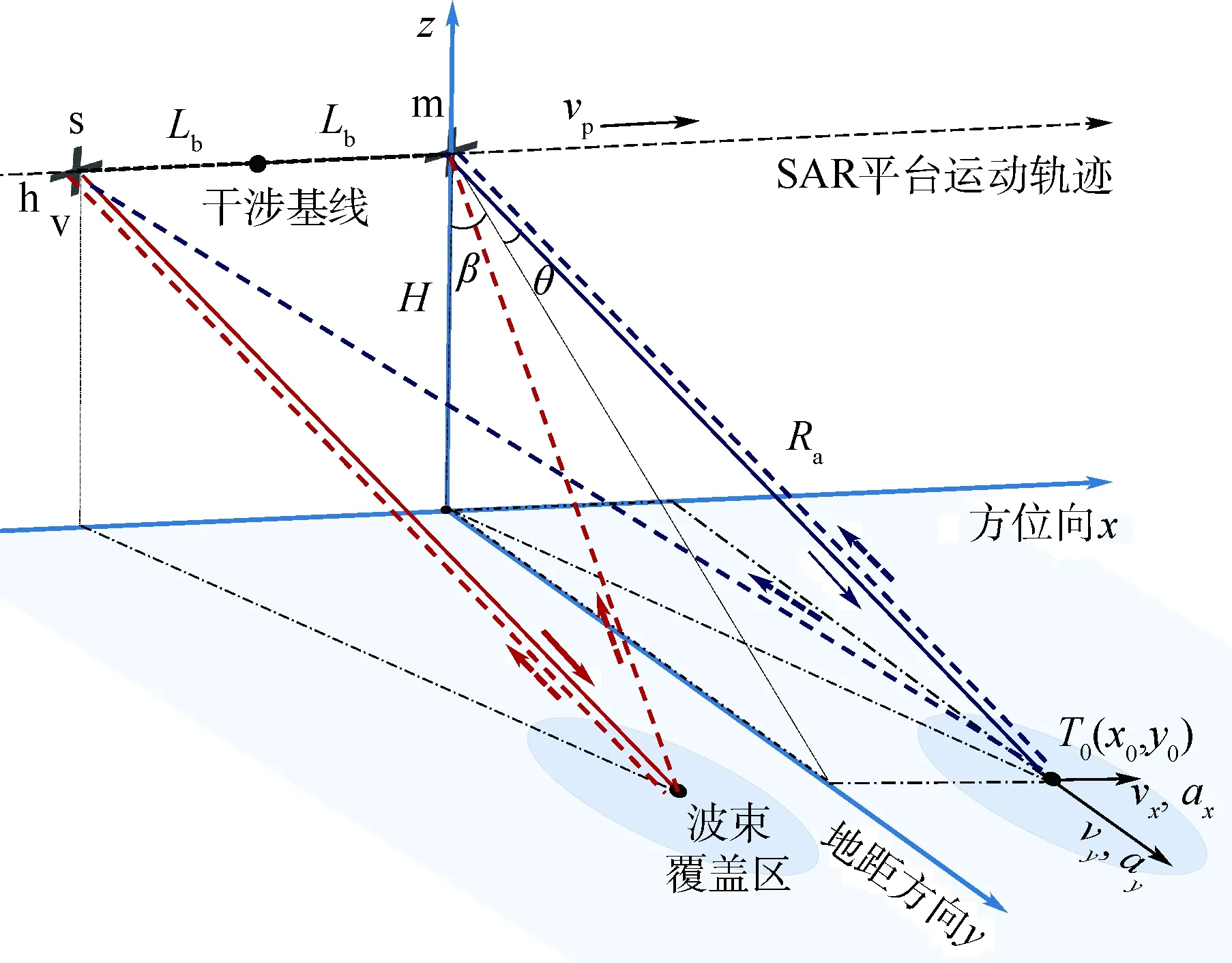
图1 单基线AT-POLINSAR成像几何示意图Fig.1 Geometry schematic diagram of single-baseline AT-POLINSAR acquisition

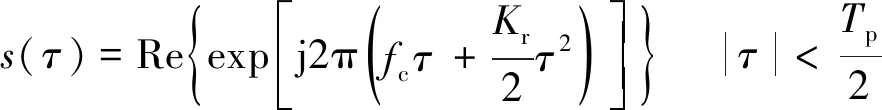
(1)

式中：τ为合成孔径处理的快时间；fc为发射信号载频；Kr为线性调频率；Tp为脉冲宽度；|·|表示取绝对值算；Re{·}表示取实部运算。为讨论方便，下文SAR信号处理时不区分极化状态。发射信号s(τ)目标T0散射后分别由m、s通道的全极化天线进行接收。

sxyi(t,τ)=Axysy(τ-τdi)=

(2)

其中：sxyi(t,τ)表示i通道x极化天线接收到的y极化状态发射信号的回波，t为慢时间，x,y∈{h,v}，i∈{m,s}，这里h、v表示极化状态，m、s则表示干涉通道类型；Axy为目标散射系数；τdi为i通道接收到回波的时延，若t时刻目标与m通道和i通道天线相位中心的瞬时斜距分别为RTm(t)与RTi(t)，则τdi=(RTm(t)+RTi(t))/c，c为光速。对i通道回波进行距离压缩，可以得到

sinc(πKrTr(τ-τdi))

(3)

其中：sinc(·)表示冲激响应函数；Tr为脉冲重复时间；λ为载波波长，对瞬时斜距进行抛物线近似[20]，i通道回波的相位即为

(4)

式中：R0为最短距离[20]，mi的下标i=m或s，mm=0，ms=1。对式(4)的信号进行方位向压缩，并忽略幅度系数，可以得到目标在目标存在的某一固定距离单元内的复图像为

(5)

其中：u为方位向像素；ux0为静止目标方位向像素位置；Δu=ΔX/ΔRx为目标偏移像素数，ΔRx为方位向分辨率，ΔX为方位向偏移距离，且ΔX=(x0vx+y0vy)/vp。再对前后通道各极化回波进行干涉处理可得

(6)

式中：Ixy-xy(u)也被称为ATI干涉图；Ta为合成孔径时间，从式(6)可得目标的干涉相位φi表达式为

(7)

1.2 AT-POLINSAR系统极化矢量干涉模型

(8)

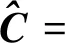
(9)

(10)

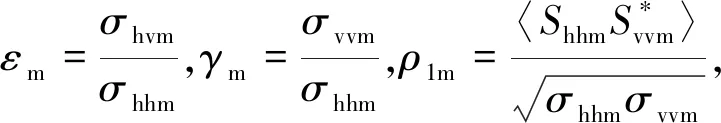
(11)

采用R进行表示的优势在于能够同时分析极化通道与干涉通道之间的相干度，且二者都能用于区分运动目标与静止目标。因而，对于单极化SAR ATI来说，以hh极化回波(h极化发射、h极化接收)为例，只需要考虑c11、c33即可。在式(9)的复高斯分布假设下，C将服从复Wishart分布[5-6]：

(12)

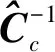
2 极化矢量干涉降维

由第1节的信号模型可知，相较于传统的极化SAR或干涉SAR，AT-POLINSAR信号处理维度急剧增加，为从其回波中检测出运动目标并估计运动状态，需要对高维极化干涉矢量数据进行降维处理，本节在回顾经典的最优极化干涉降维方法的基础上，提出了一种新的次优极化干涉降维方法。

2.1 经典最优极化干涉降维方法

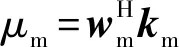
(13)

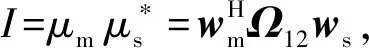
(14)

对于式(14)需要说明的是，相干度的任意损失都将引起干涉相位差估计精度的下降，因而“信号s1之间的与s2相干度ρ越大，干涉相位φi的估计就越准确”[1]。为获得最大相干度ρmax，Cloude和Papathanassiou[14]首次提出通过式(15)求解最优权矢量wm与ws的方法：

(15)

通过式(15)，可以求得km与ks的最优加权矢量分别为wm,opt与ws,opt，利用最优权矢量加权得到的新的合成极化状态μm,opt与μs,opt称为最优极化，同样还可得到最优干涉矩阵Jopt，最优干涉图Iopt以及最优干涉相位φi,opt。

2.2 基于背景杂波平均相干度最优的次优极化干涉降维新方法

传统的干涉图模型之所以不再适用于最优极化状态，是因为极化矢量km和ks最优加权矢量wm,opt与ws,opt是从每一像素单元逐一计算得到的[16]，而这种非线性的加权系数会严重影响最优干涉图的分布类型和分布函数的复杂度。但如果对整副全极化图像采用统一的线性加权矢量进行降维，分布推导的问题将可得到简化，但线性加权矢量的选取并不是任意的，其必须满足一定的准则。本文为对极化数据线性降维处理并使其降维后的杂波背景区域仍然能够像最优干涉那样达到较高的相干度，提出了针对背景杂波的次优干涉相干度准则(Suboptimal Interferometric Coherence Principle,SICP)。

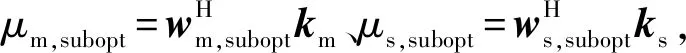
(16)

式中：μ=[μm,suboptμm,subopt]T;θ为潜在的干涉相位，对于静止杂波背景θ=0，对于运动目标θ与其径向速度有关。由式(16)，定义杂波背景区域的平均相干度为

(17)

(18)

对其求偏导，得

(19)

(20)

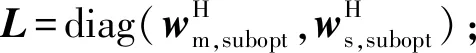
(21)

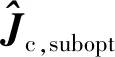
p(ξ)=

(22)

p(ψ-θ)=

(23)

式(22)中：I0(·)与Kn-1(·)分别为第1类和第2类修正的贝塞尔函数，二者的阶数分别为0阶与n-1阶[22]。式(23)中：-π<ψ≤π；2F1为广义超几何函数，分布函数的最大取值是ψ=θ，对于静止杂波背景而言θ=0 rad。对AT-POLINSAR分布式杂波进行仿真，可以得到式(22)和式(23)的理论PDF曲线对实验数据统计直方图，拟合效果如图2(a)和(b)所示，由图可见单极化干涉图统计分布理论对次优极化的适用性。文献[23]对基于干涉图的自动检测算法进行了研究，提出了检测性能较优的利用幅度相位进行联合检测的M&P检测量并推导了检测量所服从的S分布[见文献[23]式(6)～ 式(13)]。本文将M&P检测量应用于次优极化干涉图幅度、相位并将其命名为次优极化检测量(SICD)，采用仿真实验可以得到S分布对次优极化SICD检测量的统计分布拟合效果如图2(c)所示。

图2(a)～(c)所示的拟合效果充分验证了式(21)结论的正确性，表明次优极化干涉与单极化干涉具有相同的统计分布类型，因而可直接将单极化多通道SAR慢动目标检测方法应用到次优极化进行慢动目标CFAR检测。图2(d)为仿真得到的各单极化状态、最优极化状态、次优极化状态的相干度统计分布，由图可知，次优极化同样 能够达到较高的相干度，从而可以提高分布式杂波背景的相位估计精度。

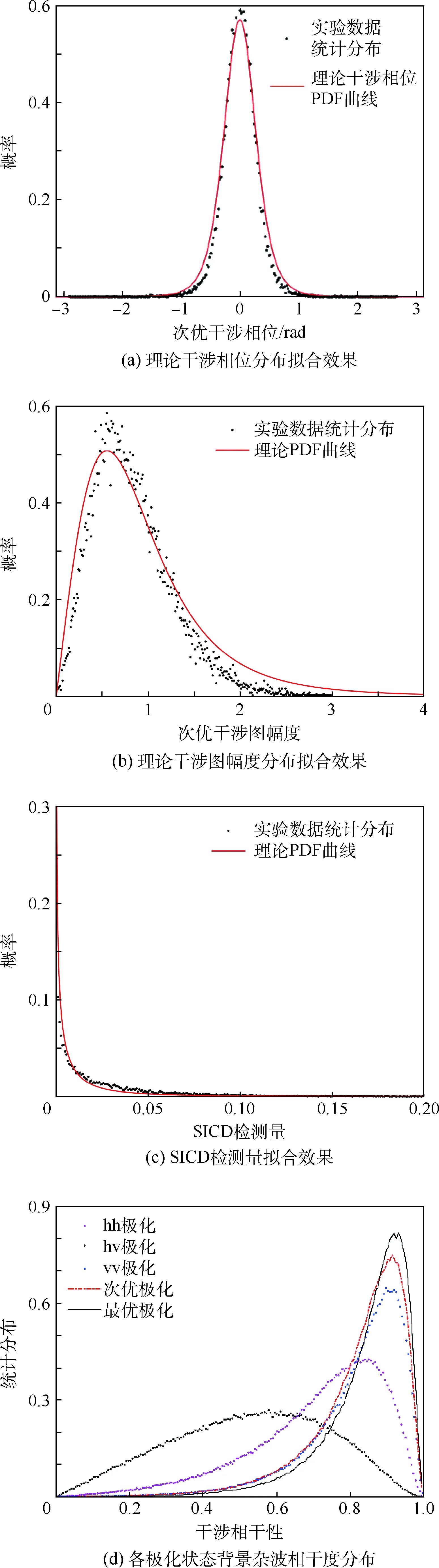
图2 次优极化统计分布Fig.2 Statistical distribution of suboptimal polarization

图3为hh单极化与次优极化的干涉图在极坐标系下的二维分布散点图(图中径向表示相干度幅度，紫色数字标注)，从图中也看出上述结论。对比图3(a)、(b)可以发现,次优干涉图的杂波分布比较集中，与目标之间的区分度明显提高，这也是次有干涉准则能够利用全极化优势以提高检测性能的原因。但需要注意的是，由于目标采用了与杂波相同的加权系数，其相干度往往不能达到最优，干涉相位中心也会发生随机的偏移，目标干涉相干度与相估计中心偏移的方向、大小与杂波特性密切相关，但总的来说，采用这种降维方式可较充分地利用全极化信息以提高运动目标检测时的信杂比。

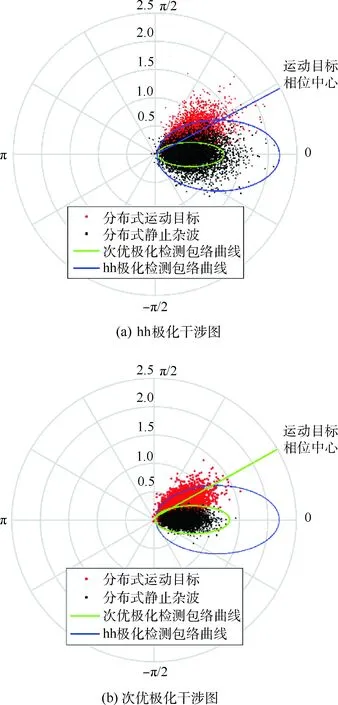
图3 干涉图二维散布特性Fig.3 2D scatter characteristics of interferograms

3 AT-POLINSAR慢小目标CFAR检测

3.1 基于SICP的慢小目标CFAR检测流程

第2节讨论了次优极化的统计特性及干涉图散布特性，结果表明现有单极化AT-INSAR慢动目标CFAR检测方法亦适用于次优极化，因而采用SICP准则对AT-POLINSAR进行慢动目标检测的流程可归纳为图4所示。

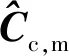
2) 将wm,subopt与ws,subopt分别应用到前后通道的全极化图像，矢像加权结果作为“次优极化”输出，即μm,subopt与μs,subopt。

3) 对前后干涉通道应用慢动目标检测算法进行慢动目标检测。

3.2 检测实验与结果

3.2.1 蒙特卡罗仿真实验

为检验次优极化的检测性能，首先将次优检测与单极化检测、全极化LRT方法[17]进行性能对比。采用蒙特卡罗实验，对文献[23]中单极化干涉相位检测器、天线相位中心偏置(DPCA)检测器、双曲线检测器以及M&P检测器应用到次优极化时的检测性能接收机工作特性(ROC)曲线进行仿真分析。实验前首先需要对AT-POLINSAR进行数据仿真，本文借鉴了文献[24]的数据生成方法对AT-POLINSAR分布式杂波与目标数据进行仿真：即产生6维相互独立的复高斯分布数据后对其进行二维相关滤波得到服从6维联合复高斯分布的干涉矢量回波序列。但与文献[24]不同的是，本文采用特征值分解方法代替Choleskey分解方法进行6维复高斯分布序列的产生，从而降低了对干涉协方差矩阵正定性的要求，只需要满足半正定即可对分布式目标或杂波的回波数据进行仿真。为使比较更有针对性，数据仿真的关键参数参考文献[17]进行设置，信杂比(Target-to-Clutter Ratio,TCR)、目标运动速度等参数如表1所示，其中雷达平台运动速度为126 m/s，重复观测时间为1.6 ms。

表1中，TCR为hh极化状态下的目标与杂波的RCS之比；信噪比(Signal-to-Noise Ratio，SNR)参数用于计算各单极化状态下顺轨干涉的相干度，即还需手动设置杂波与目标极化相干矩 阵RC,RT(但不是任意地选取)，本文假设目标交叉极化之间的相干度比杂波低，将RC与RT设为

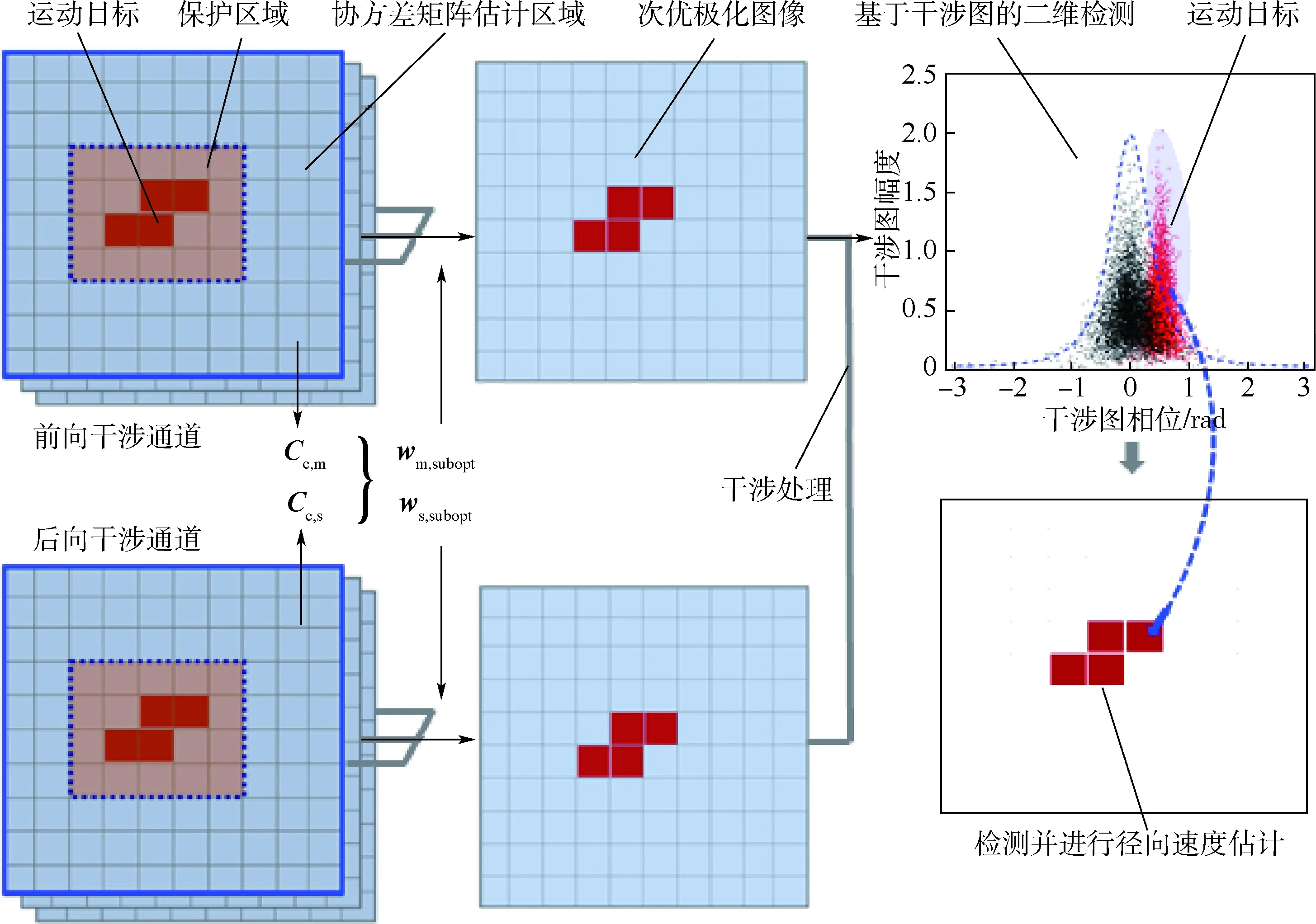
图4 采用SICP进行运动目标检测流程图Fig.4 Flowchart of moving target detection using SICP

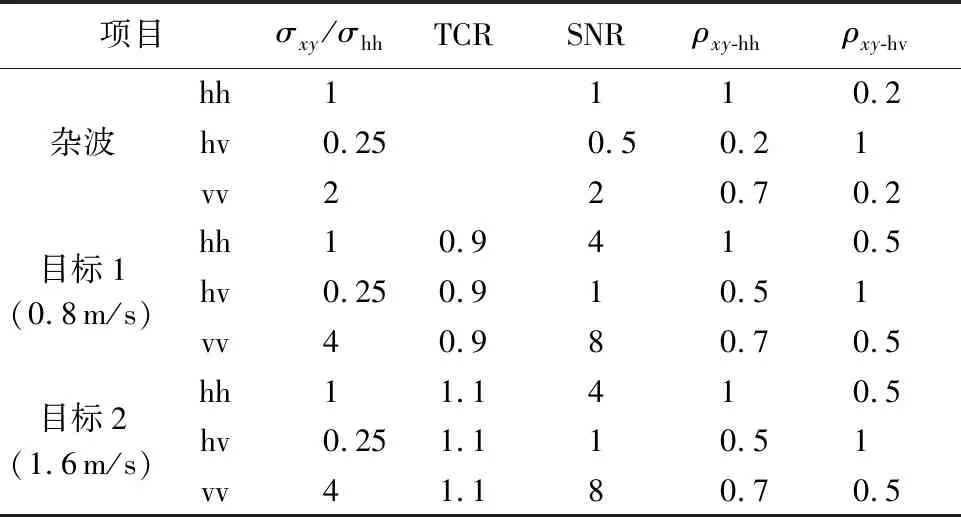
项目σxy/σhhTCRSNRρxy-hhρxy-hv杂波hh1110.2hv0.250.50.21vv220.70.2目标1(0.8m/s)hh10.9410.5hv0.250.910.51vv40.980.70.5目标2(1.6m/s)hh11.1410.5hv0.251.110.51vv41.180.70.5

(24)

由上述参数即可对AT-POLINSAR在低TCR条件下的慢动目标和杂波图像进行仿真，对仿真数据进行4视处理，分别采用次优极化、单极化对目标1、2进行107次的蒙特卡罗检测试验，可以得到如图5所示的ROC曲线。文献[20]指出，实际应用中对于ROC曲线只需要关注其低虚警区间，如(10-5,10-3)。因而由图5可得，对于当前2类试验场景，次优极化检测性能排序依次为LRT>SICD>DPCA>双曲线检测器测器。另外，还能发现全极化信息对每一类检测器所带来的检测性能增益是不同的，但总的来说，各检测器均能

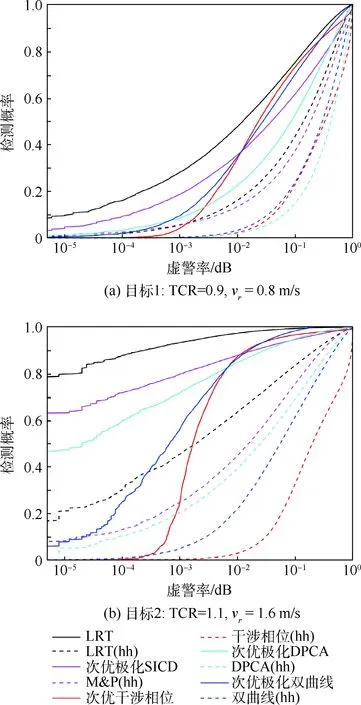
图5 ROC曲线仿真结果Fig.5 Simulated curves of ROC

通过次优极化提高检测概率。

3.2.2 场景检测实验

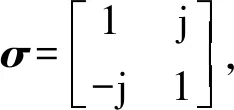
下面进行场景图像检测实验。重新对表2中的4个点目标进行信号级成像仿真，得如图7(a)所示点目标响应图像，然后设置TCR=1，得到图7(e)所示的带有杂波背景的AT-POLINSAR场景图像，由图知，此时所有目标均淹没于杂波背景中，故传统单通道幅度检测已无法对目标进行提取。现首先对AT-POLINSAR场景图像的hh极化通道应用M&P检测器，得到图6(b)所示的检测量输出；然后利用SICP方法获得求解次优极化，并对次优极化应用DPCA、SICD，可以得到如图7(c)、(d)所示的SICD输出。经计算，此时M&P(hh极化)、DPCA(次优极化)、SICD对目标2的TCR输出分别为4.77、13.11、17.16 dB，对目标3的TCR输出分别为11.25、13.52、17.39 dB。

最后，设置虚警率Pfa=10-4，对图7(b)～ (d)所示检测量输出进行CFAR检测，可以得到如图7(f)～(h)所示的检测结果，对比可见，2次优极化检测器对目标区域的检测结果较为完整，且无运动目标漏警发生，而单极化检测器中检测性能较优的M&P检测量则产生了一次漏警，未能检测出目标2。通过次优极化，AT-POLINSAR不仅能够提高对低信杂比条件下慢动的目标检测概率，还可利用全极化信息对检测出的运动目标进行最优相位估计，对慢动目标的径向速度进行高精度的估计，从而计算并校正方位向的成像位置偏移，即运动目标成像，如图7(h)所示。

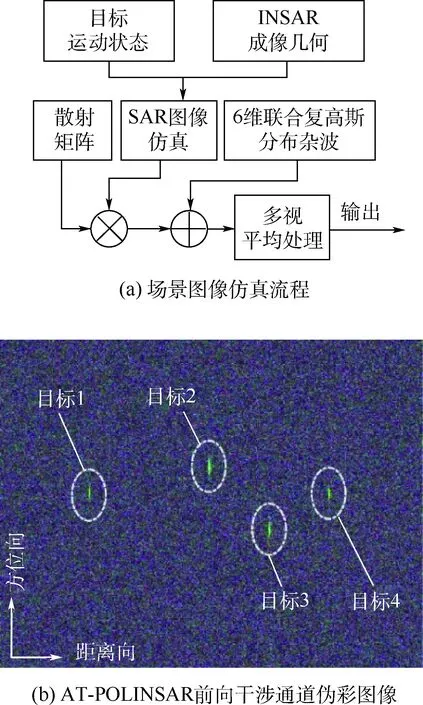
图6 场景图像仿真流程和仿真结果Fig.6 Generated flow and result of simulated scene image

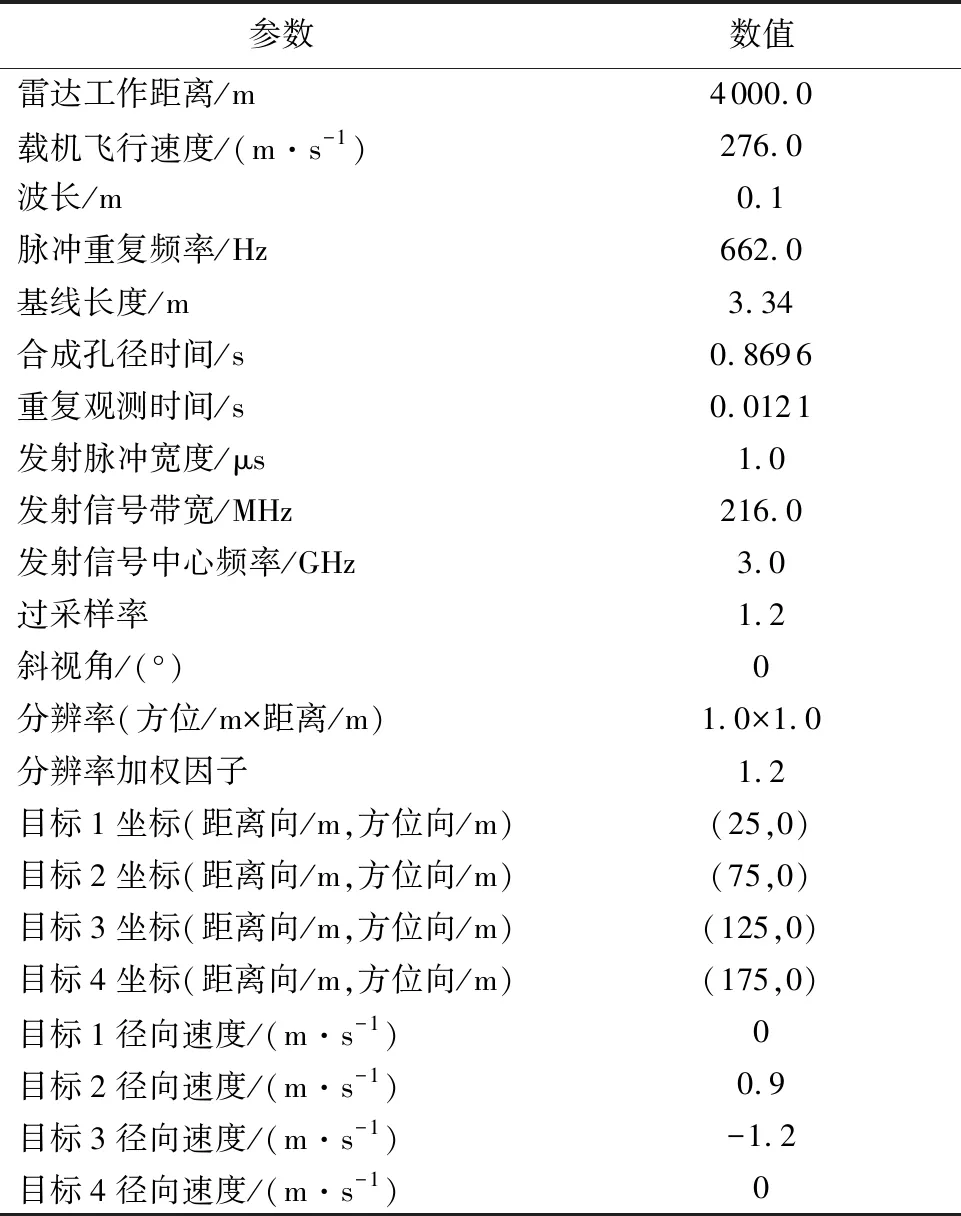
参数数值雷达工作距离/m4000.0载机飞行速度/(m·s-1)276.0波长/m0.1脉冲重复频率/Hz662.0基线长度/m3.34合成孔径时间/s0.8696重复观测时间/s0.0121发射脉冲宽度/μs1.0发射信号带宽/MHz216.0发射信号中心频率/GHz3.0过采样率1.2斜视角/(°)0分辨率(方位/m×距离/m)1.0×1.0分辨率加权因子1.2目标1坐标(距离向/m,方位向/m)(25,0)目标2坐标(距离向/m,方位向/m)(75,0)目标3坐标(距离向/m,方位向/m)(125,0)目标4坐标(距离向/m,方位向/m)(175,0)目标1径向速度/(m·s-1)0目标2径向速度/(m·s-1)0.9目标3径向速度/(m·s-1)-1.2目标4径向速度/(m·s-1)0

注：成像算法为距离多普勒； 杂波类型为复Wishart。

3.2.3 AT-POLINSAR速度估计精度

采用次优极化方法对目标的径向运动速度进行估计，需要先对图像进行GMTI，然后再对检测结果中心区域重新进行最优干涉处理和径向速估计，这是由于SICP对均匀图像背景应用统一的权矢量，会导致目标像素位置处的干涉相位具有一定的偏差。虽然采用这种二次估计的速度估计流程不如单极化情形速度提取的方便，但却能充分利用全极化信息，图8为目标径向速度估计相对误差曲线，从图中可见，在各个测试速度点上，利用AT-POLINSAR全极化信息进行相位估计，均能达到最优的径向速度估计精度(亦可验证文献[14]中“干涉相干度越高，相位估计越准确”的结论)。

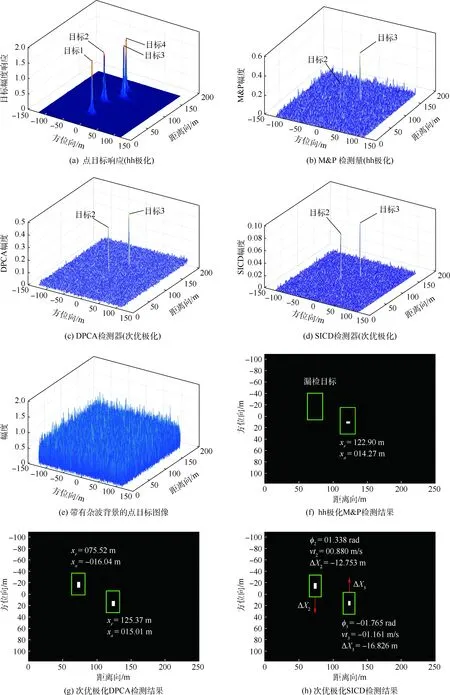
图7 AT-POLINSAR信号级仿真图像和不同检测算法的检测结果Fig.7 Signal level simulation image AT-POLINSAR and its detection results by different algorithms

3.2.4 极化干涉协方差矩阵估计点数的选取

背景杂波极化干涉协方差矩阵的估计是SICP处理的重要步骤，协方差矩阵的估计精度会直接影响次优极化干涉相干度及慢动目标CFAR检测器的检测性能，如图9所示。从图9的不同估计点数下相干度分布和SICD检测性能ROC曲线结果可以发现，对于常用的4视处理极化顺轨干涉SAR图像，估计点数选择64即可获取较高的杂波相干度和慢动目标检测性能，因而3.2节开展实验时，SICP处理选用8×8窗口对协方差矩阵进行估计。

图8 目标径向速度估计相对误差Fig.8 Relative estimation error of target radial velocity

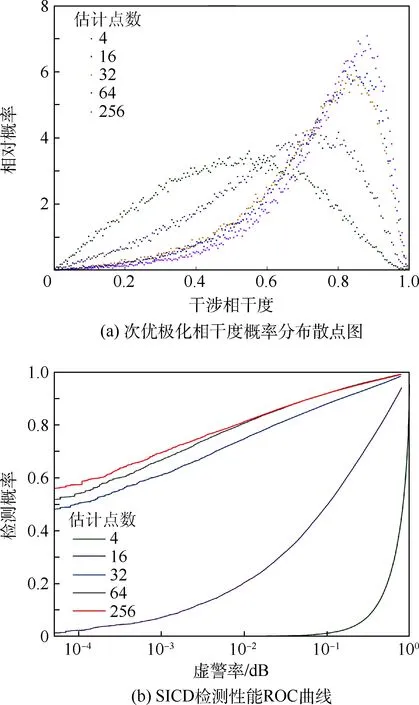
图9 估计点数对SICP性能的影响Fig.9 Performance of SICP vs. estimation point number

4 结 论

本文对如何利用AT-POLINSAR进行慢动目标CFAR检测的问题进行了研究。在对单基线AT-POLINSAR进行回波建模的基础上，针对其高维矢量干涉数据提出了基于次优干涉相干度准则。实验结果表明：

1) 次优极化能使杂波背景与目标均获取较高的相干度，但目标的相干度取值与目标特性有关。

2) 次优极化因其具有线性加权矢量,故统计分布类型与单极化相同，从而单极化AT-INSAR慢动目标检测理论能够通过其扩展至全极化并实现AT-POLINSAR的慢动目标CFAR检测。

3) 将单极化检测器应用到次优极化，检测器的性能排序与单极化情形基本一致，但通过全极化方法能显著提高干涉系统对慢小目标的检测概率。

AT-POLINSAR在慢小目标CFAR检测方面具有绝对的优势，但需要指出的是，目前仍然没有实际的AT-POLINSAR系统，为快速获取AT-POLINSAR半实测等效数据进行检测算法研究，并将极化干涉方法应用于实际POLSAR系统的GMTI，在下一步的研究中可参考文献[25]的单通道ATI方法展开单通道POLSAR ATI的研究。