单箱三室宽箱梁桥有效翼缘分布宽度研究

(中铁一院集团新疆铁道勘察设计院有限公司 新疆 乌鲁木齐 830011)

引言

箱梁由于其结构特点，在道路交通得到了大量的应用，为了满足桥面宽度的要求，近年来单箱多室箱梁桥也被人们更多地采用。箱梁在受弯时由于剪力滞效应[1-3]的存在，导致弯曲正应力的横向分布呈曲线形式，因此一般采用“有效翼缘分布宽度”的方法进行计算处理[4-6]。

目前一般的研究只针对特定的箱梁桥展开计算，没有通用性。祝明桥按照1:6缩尺比例进行了混凝土箱梁模型受弯性能试验，并通过ANSYS分析，给出了翼缘有效宽度计算系数的计算公式[7]。张彦玲采用能量变分法推导了反向集中荷载作用下截面应力的解析解，计算了组合梁负弯矩区的有效翼缘宽度，将计算结果与试验结果进行了对比[8]。我国《钢筋混凝土及预应力混凝土桥涵设计规范》第4.2.3节对箱梁有效分布宽度做出了规定，它使用“二曲线+等效简支跨长”的计算模式，其中两条曲线以单箱单室梁桥作为基础进行绘制，但没有明确指出对于单项三室箱梁桥是否适用的问题。因此本文针对单箱三室箱梁桥，通过引入合理取值的随机参数，随机生成有限元模型进行分析，寻求其有效翼缘分布宽度统计规律。

一、箱梁有效翼缘分布宽度理论

箱梁的有效翼缘分布宽度，是以翼板和腹板交接处的最大正应力为标准时的翼板折算宽度，它的提出是为了使初等梁理论能应用于解决混混凝土箱梁正截面受弯承载力计算问题，使得箱梁相关计算能简单化。其数学表达式为：

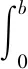
(1)

式(1)中，be为翼缘的有效分布宽度；b为翼缘的实际宽度；t为翼缘的实际厚度，σ为翼缘的实际正应力；σmax为翼缘的实际正应力峰值。

由于实际箱梁桥宽度的随机性，导致有效翼缘分布宽度也呈现随机分布，不利于整体变化规律的把握。因此按照规范JTG D62-2004方式，以有效宽度和实际宽度之比作为横坐标、实际宽度与等效简支跨长之比作为纵坐标，统计得到了单箱三室箱梁在不同跨径、不同翼缘宽度下有效宽度的分布规律。

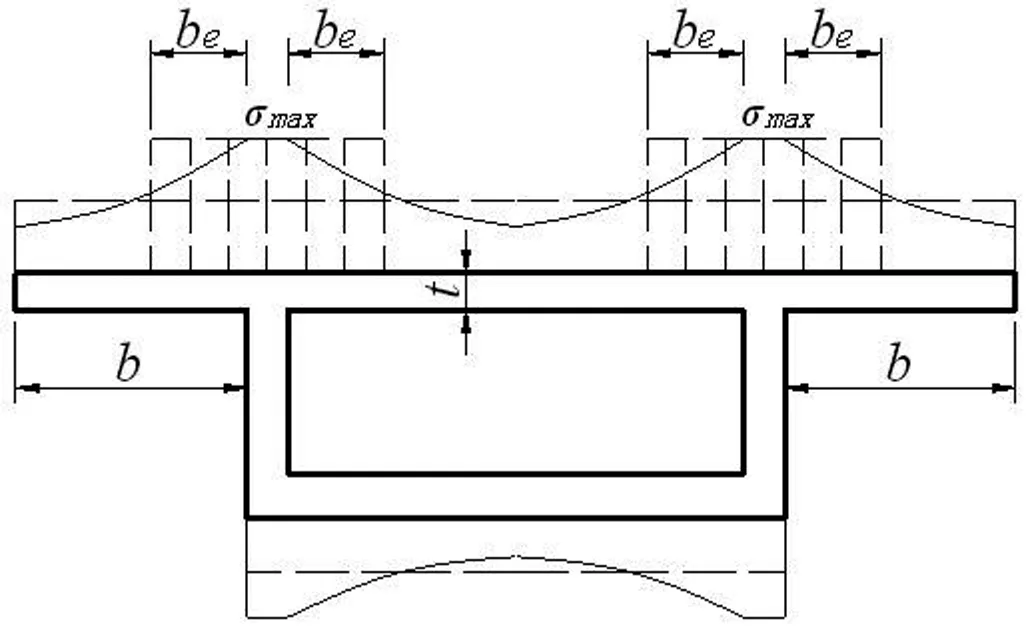
图1 有效翼缘分布宽度图示

二、单箱三室简支梁桥有效翼缘分布宽度研究

研究单箱三室箱梁有效宽度分布规律，要有大量数据作为基础。对实际桥梁结构，箱梁顶底板厚度相对与桥梁整体来说很小，属于薄壁结构，因此选用SHELL63板单元建立有限元模型，它能够反映桥梁结构整体的受力情况，便于有效翼缘分布宽度规律统计时使用。如图2所示，以bi表示各板的实际宽度，bmi表示各板的有效宽度。

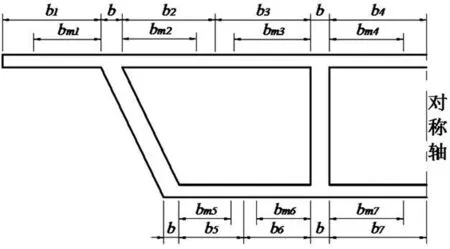
图2 三室箱梁有效宽度图示

(一)各项参数的确定

要建立合理的箱梁计算模型，首先需确定箱梁桥合理的参数取值，包括跨径、高跨比、桥面宽度、顶底板厚度、腹板厚度等。只有确保各项参数取值合理，才能建立正确的有限元模型，得出正确的结果。为了研究方便，选择等截面箱梁作为研究对象，各项参数根据规范以及各种研究资料和成桥资料确定。

(1)跨径

JTG D62-2004规范9.3.1条指出，梁的跨径根据目前较多采用的最大跨径概括得出。目前，装配式钢筋混凝土箱梁的常用跨径在8m～20m，等高度箱梁适用于中等跨径20m～60m，另外《箱型梁桥设计理论》指出，公路桥梁采用单箱或多箱的截面形式，最大跨径可达到76m，本文选用跨径10m～60m进行研究。

(2)高跨比

在梁式桥当中，桥梁高度与跨径之比称为高跨比，在装配式简支梁桥结果中其取值一般在1/11～1/18之间，在预应力混凝土桥梁中一般采用1/15～1/25的取值范围，等高度连续梁一般在1/16～1/26之间变动，并且在跨径偏大时一般取用较小的比值，综上选用1/10～1/25的取值区间。

(3)顶底板厚度

JTG D62-2004第9.3.3条规定：箱形截面梁顶、底板的中部厚度，不应小于板净跨径的1/30，且不应小于200mm。本文为了建模方便，决定选用等高度箱梁进行有效翼缘分布宽度研究，顶板厚度选用200～300mm。底板厚度采用200～250mm。

(4)腹板厚度

箱梁腹板主要承受剪力及主拉应力，并承受局部荷载产生的横向弯曲，中小跨径箱梁跨中腹板厚度一般取40～60cm，支点腹板厚度一般取60～80cm，另外参照已建成桥梁资料，一般腹板厚度取得较大，因此腹板厚度采用400～700mm。

(5)桥面宽度

箱型梁桥桥面宽度主要根据所要布置的车道确定，按照设计速度的不同，车道宽度从3.75到3.0m变化，而三室箱梁一般用于双向四车道及以上的交通中，因此取b2/b3/b4/b7在2～4.5m范围内取值，b1悬臂板取b2的0.5～1.0倍，腹板角度取45～90°。

(6)连续梁桥边中跨比

连续梁桥边跨与中跨的跨径之比称为边中跨比，参照各国对于边中跨比取值的规定，中国一般取0.6～0.65，美国允许取值范围为0.5～0.8，为了统计规律的需要，本文取边中跨比0.5～0.8进行研究。

(二)APDL参数化模型的建立

通过应用APDL参数化设计语言[9,10]，首先定义箱梁关键参数范围，用rand命令随机取值，后按照点线面的顺序生成随机的箱梁有限元模型，自由度约束加在腹板中性轴位置，同时借助do循环得到需求数量的有限元模型，get命令提取相应数据，cfopen命令存储数据。为判断建立模型的正确性，在建模同时加入BEAM188梁单元建立同尺寸对比模型，桥梁纵向为整体坐标系z轴，横桥向为x轴，竖向为y轴，建立有限元模型，运行计算后提取简支梁跨中最大挠度即箱梁在荷载下的最大y向位移作为对比项。

(1)板单元模型

(2)梁单元模型

剪力滞效应是箱梁在受弯时截面表现出的特性，剪力滞效应与荷载大小没有直接关系，但是施加的荷载过小又会导致剪力滞效应不明显，因此综合考虑施加440kN的荷载于最不利位置截面进行求解计算。

(1)简支梁纵向加载

(2)连续梁中跨纵向加载

(4)连续梁边跨纵向加载

(2)横向加载

三、结果分析

(一)挠度对比

模型建立完毕运行计算后，提取40组不同箱梁参数控制下的两种单元模型跨中最大挠度做对比。由图3可知，两种单元模型跨中最大挠度很接近，可以判定模型建立正确。

图3 挠度对比图

(二)模型数据处理结果

下图5为规范规定的有效翼缘分布宽度曲线图，其中ρf曲线适用于梁的跨中梁段截面，ρs曲线适用于支点及附近梁段截面。

根据模型应力数据，由公式(1)计算得到箱梁各板块的有效翼缘分布宽度。对计算所得数据依照规范方式整理成曲线，如下图6所示。

图5 ρf、ρs曲线图

(1)简支梁跨中梁段有效宽度图示

(2)简支梁支点梁段有效宽度图示

(3)连续梁跨中梁段有效宽度图示

(4)连续梁中支点梁段有效宽度图示

(5)连续梁边支点梁段有效宽度图示

由图6得出，对于单项三室箱梁，除连续梁跨中梁段的有效翼缘分布宽度计算曲线和规范曲线基本重合外，另外四条曲线都与规范曲线有较大差距，因此规范条文不能直接用于三室箱梁的设计计算。此外，拟合曲线两侧分布有很多数据点，为保证安全，还需对曲线进行修正。

(三)曲线修正

参照混凝土强度保证率的思想，结合本文研究内容，当样本点处于拟合曲线左侧时，在相同宽跨比时，拟合曲线的有效宽度比取值比样本点大，用于设计时是偏于不安全的，只有使95%以上的样本点处于曲线右侧，才能保证在95%的情况下结构的安全性。

图7 三室箱梁有效翼缘宽度建议取值曲线

图7中第一条曲线为单箱三室简支箱梁和连续箱梁跨中部分梁段的有效翼缘分布宽度的建议取值曲线，第二条为简支箱梁支点梁段和连续箱梁边支点梁段的有效宽度的建议取值曲线，第三条为连续箱梁中支点梁段的有效宽度的建议取值曲线。

四、结语

本文通过参数化设计语言建立大量箱梁有限元模型，根据有效翼缘分布宽度的定义计算归纳了单箱三室箱梁的有效宽度取值曲线，得到以下结论：

(1)由计算结果与规范的对比，发现对于单箱三室梁桥计算得到的有效翼缘分布宽度曲线与规范曲线不能很好的吻合，说明在实际设计中，不能直接使用规范数据。

(2)参照混凝土强度保证率的思想，对拟合曲线进行了修正，修正后的曲线具有95%以上的保证率，能保证在绝大多数情况下结构的安全性。