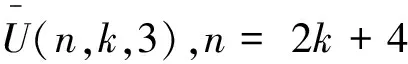恰含k个悬挂点的单圈图的极大Wiener极化指数*

胡俊伟, 邵燕灵

(中北大学 数学系,山西 太原 030051)

1 引 言

图的Wiener极化指数是由Harold在1947年研究化学分子结构提出的.目前，Wiener 极化指数已引起大家的广泛关注[1-11].设U=(V,E)是一个简单连通图，且|V|=n,|E|=m,称U为(n,m)图.若m=n+c-1,则称U为c圈图,特别当c=1时，称U为单圈图，并用c(U)表示U中圈的长度.用dU(u,v)或d(u,v)表示图U中u与v两点之间的距离.用NU(v)表示点v的邻点集合，则dU(v)=|NU(v)|为点v的度,特别的，如果dU(v)=1,则v称作U的悬挂点，一条i度悬挂路是一条内部点度均为2且两端点度分别为1和i(i≥3)的路.如果一个图U是由一个顶点v连接若干条长度至少为2的路所得到的图，则称U为类星图，点v为U的中心点.

图U的Wiener极化指数定义为图U中距离为3的点对{u,v}的数目[1-2]，记为

Wp(U)=|{{u,v}|dU(u,v)=3,u,v∈V}|

目前关于树的Wiener极化指数的研究较多，但是对于含圈图的Wiener极化指数问题的研究却很少，本文将研究具有k个悬挂点且无1长悬挂路的n阶单圈图的Wiener极化指数，通过引出五种图的变换，给出了这类图的极大Wiener极化指数，并且刻画了相应的极图.

2 引理及图的变换

引理1[1]设T=(V,E)是一个树图，则

令mi,j是树图T中一端点度为i且另一端点度为j的边的数目，则由引理1，有

引理2[4]设U=(V,E)是一个单圈图，C是U中的圈.

(i)若c(U)=3且记V(C)={v1,v2,v3},则

(ii)若c(U)=4且记V(C)={v1,v2,v3,v4},则

(iii)若c(U)≥5,则

为证明本文结果，下面定义五种单圈图的变换，并考虑变换前后单圈图的Wiener极化指数.

2.1 第I种图变换

设n≥2k+c,U是如下图所示的具有k个悬挂点且无1长悬挂路的n阶单圈图，其中U1是U的含圈子图，e=uv∈E(U),点v处连接k1条悬挂路.设图U′=U/e是图U通过对e收缩得到的，即在图U中删除边e,将点u和v合并为一点，然后在点v连接的某条悬挂路上添加一个顶点得到.称图U′是由图U经过第I种图变换(缩边变换)所得(如图1所示).

图1 第I种图变换

引理3 设n≥2k+c,图U′是由图U经过第I种图变换(缩边变换)所得(如图1所示).若c≥4,或c≥3且u不在图U的圈上，则Wp(U′)≥Wp(U).

证明令NU(u)/v={u1,u2,……,us}和NU(v)/u={v1,v2,……,vt}.考虑以下两种情形.

情形1.c≥5或点u不在圈c上时,根据引理2，有

由于

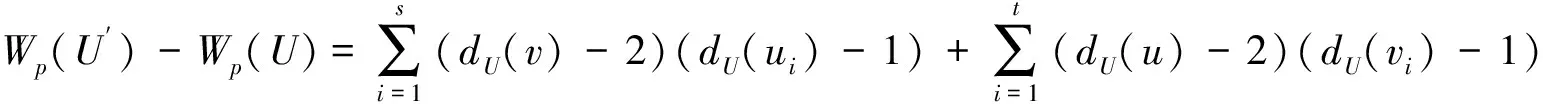
又由于dU(ui)≥2,dU(vi)≥2,则

故

因此，Wp(U′)-Wp(U)≥0.

情形2.c=4且点u在圈c上,根据引理2，有

同理由于

因此

1-(dU(u)-1)(dU(v)-1)+(2-dU(v))

由于dU(ui)≥2,dU(vi)=2,dU(u)≥3,则

故

(dU(v)-1)(dU(u)-1)+(dU(v)-3)

因此Wp(U′)-Wp(U)≥0.

当c=3且点u不在圈c上的情况已在情形1中证明，因此引理得证.

2.2 第II种图变换

设c≥4或c=3,n=2k+3,m≤c,U′(n,k,c)是在一个c长圈的m个顶点v1,v2,…,vm处分别连接k1,k2，…,km条2长或2长以上的悬挂路所得的n阶单圈图，其中k=k1+k2+…+km,设U(n,k,c)是将U′(n,k,c)的k条悬挂路全部连接到c长圈的一点处(如v1)所得的图.称图U(n,k,c)是由U′(n,k,c)经过第II种图变换所得(如图2所示).

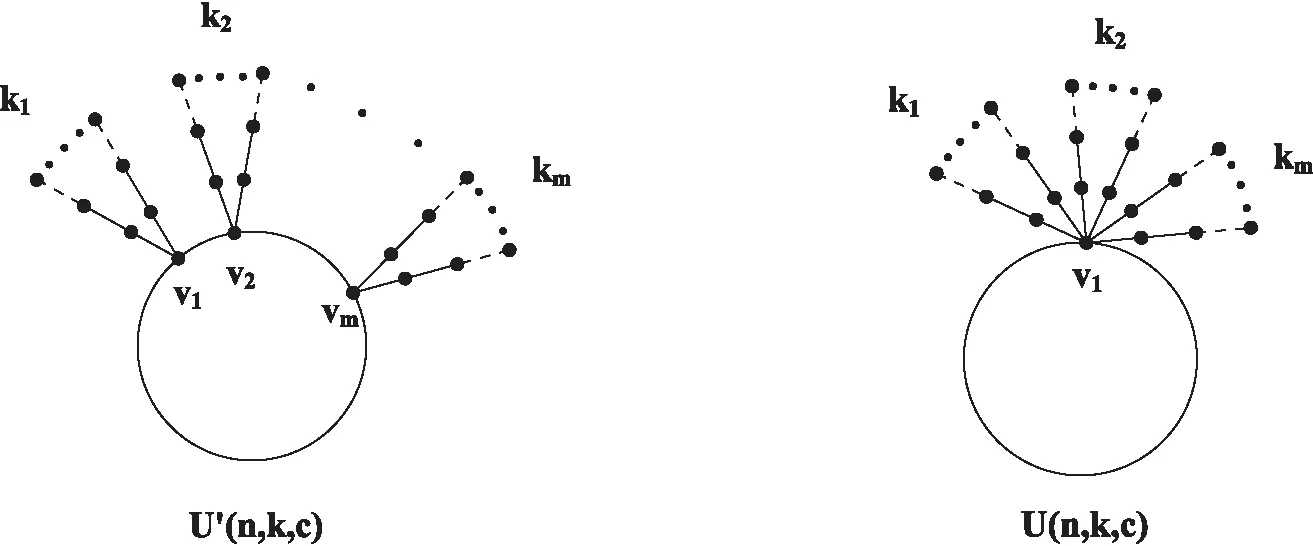
图2 第II种图变换

引理4 设c≥4或c=3,n=2k+3,m≤c, 图U(n,k,c)是由U′(n,k,c)经过第II种图变换所得n阶单圈图(如图2所示)，则Wp(U(n,k,c))>Wp(U′(n,k,c)).

证明分别记U=U(n,k,c),U′=U′(n,k,c).将Wp(U)和Wp(U′)分为三部分计算，第一部分

是悬挂路之间Wiener极化指数的值，第二部分

是悬挂树到圈上Wiener极化指数的值，第三部分

是圈上Wiener极化指数的值，则

由引理1和引理2知

(1)当c≥7时，因

Wp(U1) =(k1+k2+…+km)(k1+k2+…+km-1)+(n-2k1-2k2-…-2km-c)=

k(k-1)+n-2k-c=n+k2-3k-c

Wp(U2)=4(k1+k2+…+km)=4k

Wp(U3)=c

所以Wp(U)=n+k2+k.同理，

Wp(U1′)=k1k2+k2k3+…+km-1km+kmk1+k1(k1-1)+…+km(km-1)+

Wp(U2′)=4(k1+k2+…+km)=4k

Wp(U3′)=c

(2)当c=6时，因Wp(U2)=Wp(U2′)=4k,Wp(U3)=Wp(U3′)=3,Wp(U1)>Wp(U1′),故WP(U)-WP(U′)>0.

(3)当c=5时，因Wp(U2)=Wp(U2′)=4k,Wp(U3)=Wp(U3′)=0,Wp(U1)>Wp(U1′),故WP(U)-WP(U′)>0.

(4)当c=4时，因Wp(U2)=Wp(U2′)=3k,Wp(U3)=Wp(U3′)=0,Wp(U1)>Wp(U1′),故WP(U)-WP(U′)>0.

(5)当c=3,n=2k+3时，因Wp(U2)=Wp(U2′)=2k,Wp(U3)=Wp(U3′)=0,Wp(U1)>Wp(U1′),故WP(U)-WP(U′)>0.

综上所述，引理得证.

2.3 第III种图变换

设图U1是具有k个悬挂点、圈长为3且无1长悬挂路的n阶单圈图(如图3所示)，其中v1v2v3是一个3圈，3圈上每一点连接一些悬挂树，其中这些悬挂树可以是悬挂路，也可以是通过一条边与一个类星图中心连接.设图U2是将U1中3圈上点v2,v3处连接的悬挂树全部移到点v1处所得的图.称图U2是由U1经过第III种图变换所得(如图3所示).

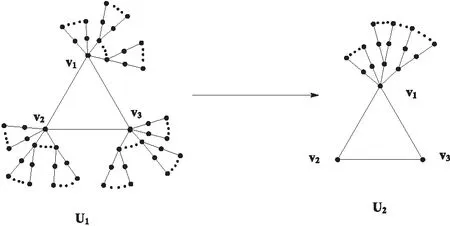
图3 第III种图变换

引理5 设图U2是由U1经过第III种图变换所得的n阶单圈图(如图3所示)，则Wp(U2)>Wp(U1).

证明设在图U1中，与v1点距离为1的点有a个，距离为2的点至少有a+m1(m1≥0)个；与v2点距离为1的点有b个，距离为2的点至少有b+m2(m2≥0)个；与v3点距离为1的点有c个，距离为2的点至少有c+m3(m3≥0)个.则

Wp(U2) -Wp(U1)=(a+b+c+1)(a+b+c+m1+m2+m3)-ab-ac-bc-

(a+1)(a+m1)-(b+1)(b+m2)-(c+1)(c+m3)

因(a+b+c+1)(a+b+c+m1+m2+m3)=(a+m1)(a+b+c+1)+(b+m2)(a+b+c+1)+(c+m3)(a+b+c+1),所以Wp(U2)-Wp(U1)>0,引理得证.

2.4 第IV种图变换

如图4所示，图U2只在点v1处连接一些悬挂树，其中这些悬挂树可以是悬挂路，也可以是通过一条边与一个类星图中心连接，设这样的类星图有m个，将每一个类星图以及与它直接连接的边记做一个分支，每个分支上分别有k1,k2，…,km条悬挂路，在悬挂路不变的情况下，设图U3是将U2上这m个分支的悬挂路均转移到一个分支上的图.称图U3是由U2经过第IV种图变换所得(如图4所示).

图4 第IV种图变换

引理6 设图U3是由U2经过第IV种图变换所得的n阶单圈图(如图4所示)，则Wp(U3)>Wp(U2).

证明假设第i个分支上的2长悬挂路的数目是最多的，从除第i个分支的其他任意一个分支取一条悬挂路转移到这个分支上，可知此时第i个分支上有ki+1条悬挂路，第j个分支上有kj-1条悬挂路，则Wiener极化指数变化为

ΔWp(U)=2ki-2(kj-1)=2(ki-kj)+2

由于ki-kj≥0,则ΔWp(U)>0,因此可知经过变化后，图的Wiener极化指数是增大的.依次将其他分支上的悬挂路均移到第i个分支上，可知Wiener极化指数是不断增大的，直到将所有分支上的悬挂路都移到这一个分支上，此时图的Wiener极化指数是最大的.证毕.

2.5 第V种图变换

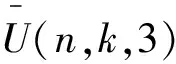
图5 第V种图变换

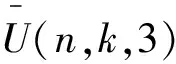
3 主要结论

定理1 设图U是具有k个悬挂点且无1长悬挂路的n阶单圈图，c(U)≥4,则

等号成立当且仅当U=U(n,k,c)(如图2所示).

证明由引理3，图U经过第一种变换(缩边变换)后，得到所有2长以上的悬挂路均分布在图U的圈上各点，再通过引理4，所有2长以上的悬挂路均集中在图U的圈上一点，用U(n,k,c)来表示所得到的图.超过2长悬挂路的点均可以转移到其中的一条悬挂路上，因为在圈长不变的情况下，这些点移动到圈图上的任何一个位置，都不会改变单圈图Wiener极化指数的值.下面根据引理1、引理2分别进行计算.

(iii)当n=2k+6时，圈图U(n,k,c)有c=4、c=5、c=6三种情况.计算得

(iv)当n≥2k+7时，c≥7.当c=7时，Wp(U(n,k,7))=n+k2+k,当c>7时，圈长的增加并不影响图U的Wiener极化指数，则Wp(U(n,k,c))=n+k2+k(c≥7).

综上所述，定理得证.

定理2 设U是具有k个悬挂点且无1长悬挂路的n阶单圈图，c(U)=3,则

证明由引理3，图U经过第一种变换(缩边变换)后，得到圈上每一点连接一些悬挂树，其中这些悬挂树可以是悬挂路，也可以是通过一条边与一个类星图中心连接.通过引理4，将所有悬挂树均集中在图U的圈上一点，通过引理5，在悬挂点不变的情况下，将各分支上的悬挂路集中到一个分支上，用U(n,k,3)来表示所得到的图.超过2长悬挂路的点均可以转移到其中的一条悬挂路上，因为在圈长不变的情况下，这些点移动到圈图上的任何一个位置，都不会改变单圈图Wiener极化指数的值.下面根据引理1、引理2分别进行计算.

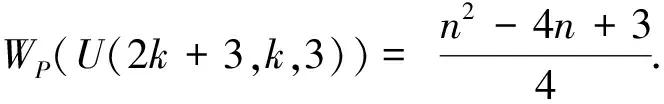
综上所述，定理得证.

将定理2中c=3的情况与定理1中c≥4的情况在阶数相同时分别进行比较，显然可得以下结论.

定理3 设U是具有k个悬挂点且无1长悬挂路的n阶单圈图，c(U)≥3,则