有限时间稳定的球杆控制系统设计
2019-04-04何标涛王建晖
黄 星,何标涛,王 涛,王建晖
(广州大学 机械与电气工程学院,广东 广州 510006)
球杆系统是高校控制实验室常见的设备,是安全性较高的开环系统,通常用来检验控制方法的效果,是经典控制方法与现代控制方法的理想研究对象[1-4]。近几年来,很多学者对球杆系统作了大量的研究,并从不同的角度提出了控制器的设计方法,主要有PID控制、滑模变结构控制和模糊控制等。其中PID控制器以其结构简单、对模型误差具有鲁棒性以及易于操作等特点,得到了广泛的应用。
在广泛的实际应用中,发现上述方法存在局限性,主要表现在系统难以实现有限时间稳定,且对强干扰过程难以实现稳定控制,从而无法实现对系统的高精度控制,甚至导致控制系统崩溃。而工业系统中,有限时间稳定性能和抗扰动性能无疑是十分重要的,因此针对有限时间稳定和抗扰动性能的研究是非常具有实际意义的工作。
本文首先对球杆系统进行数学建模和分析,设计出有限时间稳定控制器,然后通过仿真实验验证有限时间稳定控制方法的扰动性能,最后与PID控制进行对比分析,验证有限时间稳定控制方法的有效性和可行性。
1 球杆系统的建模与分析
球杆系统的机械部分主要由钢制支架、底座、小球、平衡杆、带轮、电机等部分组成[5],其闭环控制结构图如图1所示。

图1 球杆系统闭环控制结构图Fig.1 Closed-loop control structure of the Ball&beam system
图1中,实时控制电机的转动使带轮转动,带轮再带动机械结构运动,从而控制小球在导轨上运动[6]。具体地说,基于让小球在导轨上稳定运行的目的,对直流伺服电机的转速与方向进行控制以实现对带轮转动的控制,从而带动机械结构控制导轨的倾斜程度,进而达到对小球稳定运行的精准控制。
球杆系统运动示意图如图2所示。通常直流伺服电机所带的增量式码盘可以测量电机的实际转动位置,而小球的实际位置则是通过导轨上的电阻传感器测量,并进行相应的转换计算得出。图2中,电机的转动带动带轮转动θ角度,带轮又带动连杆运动,使得导轨产生α角度的偏转,从而导致小球在导轨上滚动。
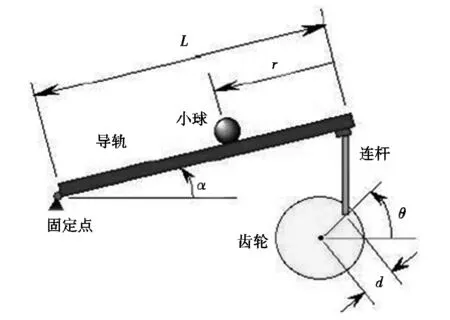
图2 球杆系统运动示意图Fig.2 Motion diagram of the Ball&beam system
图2中,连杆与带轮连接处的中心点与带轮中心点的距离记为d,mm;连杆与带轮连接处的中心点与带轮几何中心点的连线与水平线的夹角记为θ,(°),在系统运行过程中θ的大小有一定的范围限制;连杆与导轨的连接点与导轨固定点之间的距离记为L,mm。在忽略一些部件构成因素的情况下,利用经典力学理论建立球杆系统的运动学方程,近似得出导轨的倾斜角度α与带轮转角θ间关系如下:
(1)
因此,通过控制带轮上齿轮的转角θ,可以实现对小球位置的控制。球杆系统控制器的设计原理就是通过控制直流伺服电机达到对带轮转角θ的精确调整,实现对小球位置的精确控制[7]。
对球杆系统进行动力学分析,得出小球运动与其自身重力、惯量、导轨的转角α、自身的位移r之间的关系如下:
(2)
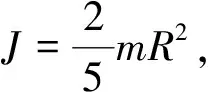
由于所建模型不需要很精确,且α的期望在0附近,故在0附近对α进行线性化,得
sinα≈α,

(3)
因此,方程(2)可以近似简化为:
(4)
将式(1)带入式(4),可得
(5)
式中,小球在导轨上的实际位移r是系统的实际输出量,带轮转动角度θ是控制的输入量[8-10]。
2 有限时间稳定控制器设计
2.1 系统状态方程描述
根据式(5),定义如下变量:
由上述定义可得
(6)


(7)
因此,控制器可以设计为:
u=-k1signy1|y1|α1-k2signy2|y2|α2
(8)

2.2 系统的稳定性分析
球杆系统要具有有限时间内稳定的特性和鲁棒性的要求。现对有限时间内球杆系统稳定性进行证明,过程如下:
选择Lyapunov函数如下:
(9)
对式(9)的Lyapunov函数求导,可得
k1sign(y1|y1|α1y2+
y2(-k1signy1|y1|α1-k2signy2|y2|α2)=
-k2signy2|y2|α2y2=
-k2|y2|1+α2
(10)

k2signy2|y2|α2
(11)
令
g1(t)=-k1signy1|y1|α1y1=
-k1|y1|1+α1
(12)
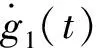
根据齐次系统定义,系统的向量场满足
f(φλ1y1,φλ2y2)=
(13)
由此可得
(14)

3 仿真结果与分析
3.1 球杆系统有限时间稳定控制模型仿真搭建
球杆系统模型可以描述如式(5)所示,即
对球杆系统模型分析后可得式(8)形式的有限时间控制器,即
u=-k1signy1|y1|α1-k2signy2|y2|α2
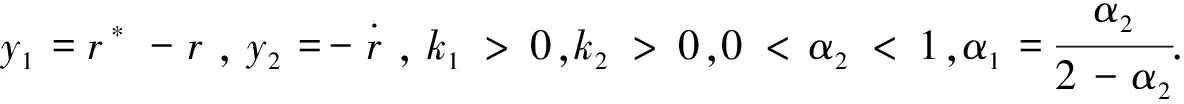
在Simulink中使用相应模块并调整参数搭建球杆系统仿真模型,如图3所示。
3.2 传统PID控制与有限时间稳定控制的对比分析
3.2.1 未加扰动分析
对图3的模型运行后得到传统的PID控制与有限时间稳定控制的响应曲线对比,如图4所示。

图3 未加入扰动时有限时间稳定控制的Simulink仿真图Fig.3 Simulink simulation diagram of undisturbance finite time stability control
对图4的响应曲线作误差分析,得到图5所示的误差分析曲线。
分析图4、图5可知:传统PID控制与有限时间稳定控制相比,有限时间稳定控制几乎没有超调量,且能够让系统在更短的时间内稳定,控制误差范围更小,符合对于有限时间稳定控制优势的理论分析。
3.2.2 加扰动分析
对已搭建好的模型稳定运行300 s后加入扰动d(t)=20sint+20cost。加入扰动后,有限时间稳定控制和PID控制在Simulink上的仿真模型分别如图6、图7所示。

图4 未加入扰动的响应曲线Fig.4 Undisturbance response curve graph
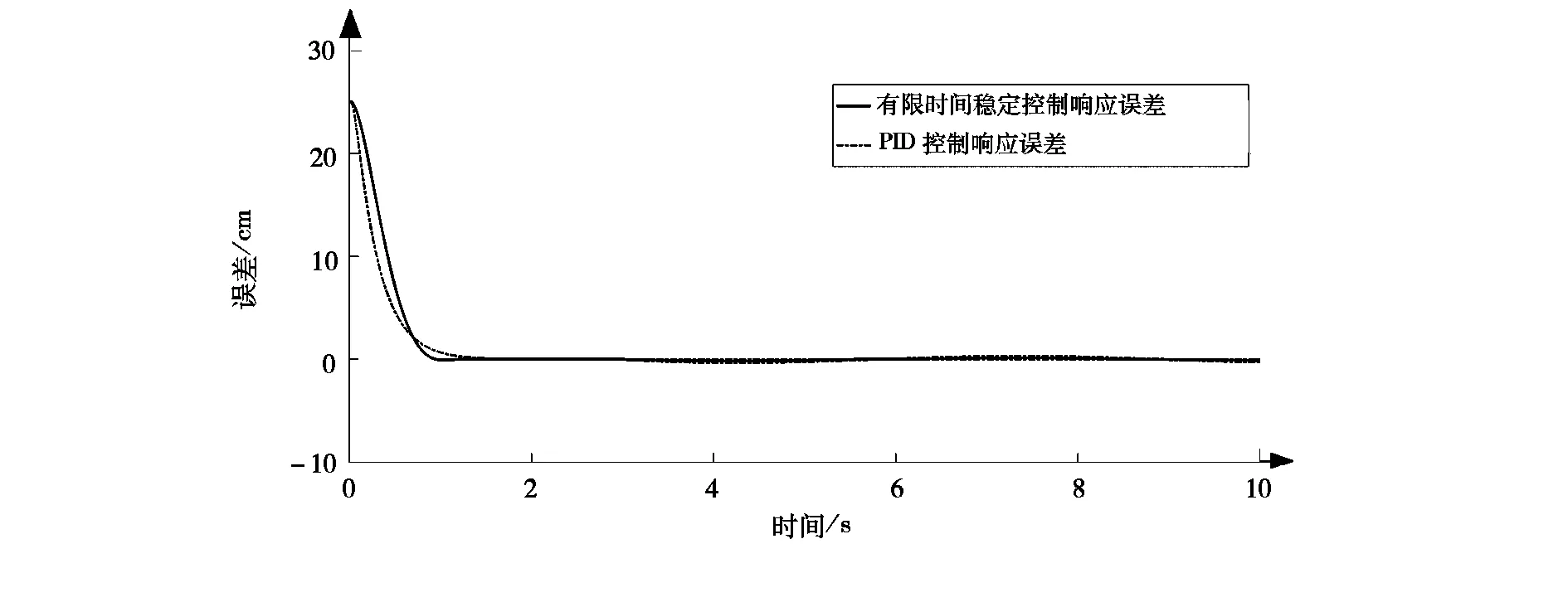
图5 未加入扰动的误差曲线Fig.5 Undisturbance response error curve graph

图6 加入扰动后有限时间稳定控制的Simulink仿真图Fig.6 Simulink simulation diagram of add disturbance finite time stability control

图7 加入扰动后PID控制的Simulink仿真图Fig.7 Simulink simulation diagram of add disturbance PD control

图8 加入扰动响应曲线Fig.8 Add disturbance response curve graph

图9 加入扰动误差曲线Fig.9 Add disturbance response error curve graph
运行后得到传统的PID控制与有限时间稳定控制的响应对比曲线如图8所示。
对图8的响应曲线作误差分析,得到图9所示的误差分析曲线。
由图8、图9可以看出:加入扰动后,PID控制系统出现轻微的振动,其振动变化幅度比有限时间稳定控制的更大,即有限时间稳定控制方法具有更强的抗干扰能力,符合有限时间稳定控制方法优势的理论分析。
4 结论
针对现有球杆系统控制方法在有限时间稳定和抗干扰能力上的不足,提出一种有限时间稳定控制的方法。基于已有的球杆系统的动力学分析,建立球杆系统的简化数学模型;结合相应的控制理论,设计出有限时间稳定控制器;最后通过仿真实验,对有限时间稳定控制和PID控制在加入扰动前后的仿真结果进行对比分析。实验结果表明,有限时间稳定控制方法能够让系统在更短的时间内稳定,同时提高了系统的抗干扰能力。因此,有限时间稳定控制方法在球杆系统上表现出的优异控制性能,能够满足现代工业系统在短时间内稳定且具有较强抗干扰能力的需求,即对有限时间稳定控制方法的研究具有非常重要的现实意义。
