弧形双悬臂梁试样裂纹扩展电测接线点布局研究
2019-04-04倪陈强赵凌燕崔英浩
倪陈强,薛 河,赵凌燕,崔英浩,王 帅
(西安科技大学机械工程学院,陕西西安710054)
0 引 言
核电压力容器及管道的应力腐蚀开裂显著降低了核电设备的设计寿命和安全性[1-5],利用含裂纹试样进行应力腐蚀裂纹扩展试验是核电站安全评价研究工作的重要组成部分之一[6-9]。应力腐蚀裂纹扩展试验中常用的试样有3点弯曲试样[10]、紧凑拉伸试样[11-12]和弧形双悬臂梁试样等,其中,弧形双悬臂梁(Contoured Double Cantilever Beam,CDCB)试样是一种特殊设计的试样,在裂纹扩展过程中可保持应力强度因子恒定[13-15]。在应力腐蚀裂纹扩展试验中,试样被放置于模拟实际工作条件的高压釜密闭环境中,对裂纹扩展很难直接观测,只能用间接方法对裂纹长度进行测量。电位降法是可用于高压釜密闭环境中的一种常用裂纹扩展监测方法[16-17],其分为直流电位降(Direct Current Potential Drop,DCPD)法和交流电位降(Alternating Current Potential Drop,ACPD)法,原理都是对被测金属试样施加激励电流(直流或交流),通过测量试样特定位置的电位差变化来确定裂纹长度变化量[18]。DCPD法不存在ACPD法的集肤效应,是裂纹扩展试验中实时测量试样裂纹动态扩展长度的主要手段[19]。裂纹长度与电位差的关系与试样形状有关,Johnson研究了无限长有限宽板中心裂纹试样的电位场,并给出了均匀电流密度条件下电位差与裂纹长度关系的解析解[20],陈篪用解析法研究了3点弯曲试样的电位场和无销钉孔紧凑拉伸试样的电位场[21]。对于各种实际试样的理论标定,一般使用有限元方法给出电位场数值解,并回归得到近似理论标定公式。Ritchie利用有限元法求得了紧凑拉伸试样的电位场,并回归得到了裂纹长度-电位差标定公式。李智军利用有限元法对含半圆表面裂纹试样的电位场进行了有限元分析,为含裂纹试样三维电位场有限元求解奠定了基础[22]。相关研究表明,表征裂纹长度的电位差信号的灵敏度和幅度不但与材料的电导率有关,还与被测试样的形状、电流加载点和电位差测量点的布局密切相关[23-25]。另外,DCPD法裂纹测量中电位差信号非常微小(微伏级)[26],再加之热电势、仪器温漂、环境电磁干扰等因素的影响,信号的准确测量面临很大困难[27-29]。因此,寻求被测试样最优接线点布局以获得最优的信号灵敏度和信号幅度,对于提高测试精度具有重要意义。文中利用有限元软件建立CDCB试样三维模型,求取不同裂纹长度下的试样三维电位场分布,从信号灵敏度,信号幅度和测点位置误差敏感度3方面对电流加载点和电位差测量点的合理选择进行研究。
1 理论基础
电位降法是基于金属材料本身导电特性测量裂纹长度的方法。如图1所示,在含裂纹试样上电位场是裂纹尺寸的函数,在恒定激励电流下,当裂纹长度发生变化时试样的电位场发生变化,通过测定裂纹两侧电位差的变化就可以求出裂纹长度的变化。电位降法一般需要4根引线,与试样形成4个接线点。在图1中,激励电流从外侧两接线点(C1,C2)通过被测试样,电位差信号从内侧两接线点(P1,P2)引出测量。
通电导体中的电位场可由拉普拉斯方程描述

式中 V为导体中任意一点的电位。对于二维平面内的电位场分布,此方程可以用共形映射法求解。Johnson首先研究了无限长有限宽板中心裂纹试样通以垂直于裂纹面恒定电流的情况,求得了电位差与裂纹长度的关系式
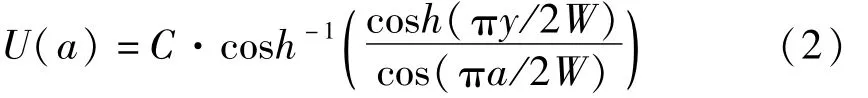
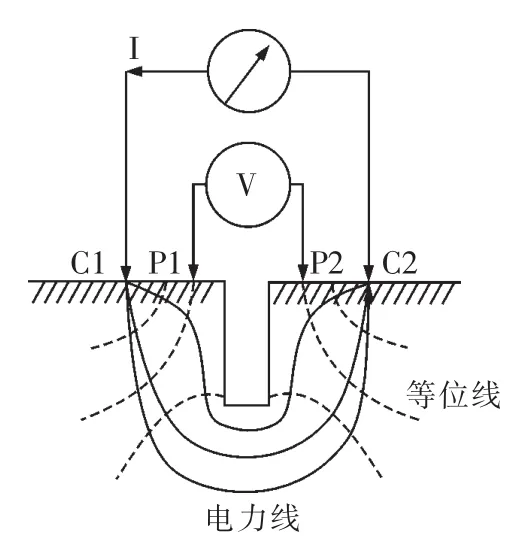
图1 直流电位降法原理Fig.1 Direct current potential drop method
式中 a为裂纹半长;y为中轴线上两测点间距离的半长;W为试样半宽;U为两测点间电位差;C为常数。单边裂纹试样可看作中心裂纹试样的一半,常数C的具体表达式由陈篪给出
式中 ρ为电阻率;I为电流;B为试样厚度。陈篪还给出了无销钉孔CT试样的近似解析解,当电流从裂纹两侧最远顶点加载且电位差从裂纹嘴处测量时,电位差为
式中 H为试样半高;W为试样宽度,其他参数同上。
CDCB试样的几何形状如图2所示,由于试样形状并非简单的等截面体,高度和宽度尺寸接近,在边界条件方面电流输入点的位置对裂纹尖端已不再相当于“远处”加载,因而现有解析公式均不能直接应用。销钉孔的存在使求解域成为非单连通区域,使解析解求取变的非常困难,而有限元法不但可以求解任意形状试样的二维电位场近似解,还可求出试样三维空间的电位场分布,结果更接近实际情况。
2 有限元模型
如图2所示,取CDCB试样公称宽度W=60 mm,取试样厚度B=16 mm,试样有限元模型使用商用有限元软件ABAQUS建立。需要注意的是裂纹长度a是从销钉孔算起的,这符合常用断裂力学试样标准中裂纹长度的规定。由于试样几何形状相对于裂纹面对称,且实际应用中电流加载点和电位差测量点一般也对称于裂纹面,所以只需建立试样1/2有限元模型,以节约计算成本和提高模型的网格质量。试样有限元网格如图3所示,单元类型为8节点线性热电耦合实体单元(DC3D8E)。为了保证计算结果准确,裂纹附近的单元尺寸被充分细化。材料属性方面,设置材料电导率为核电站压力容器结构材料中常用的304不锈钢的电导率1 388.89 S/mm.有关热传导的参数不作设置,这样ABAQUS将只进行电传导分析。
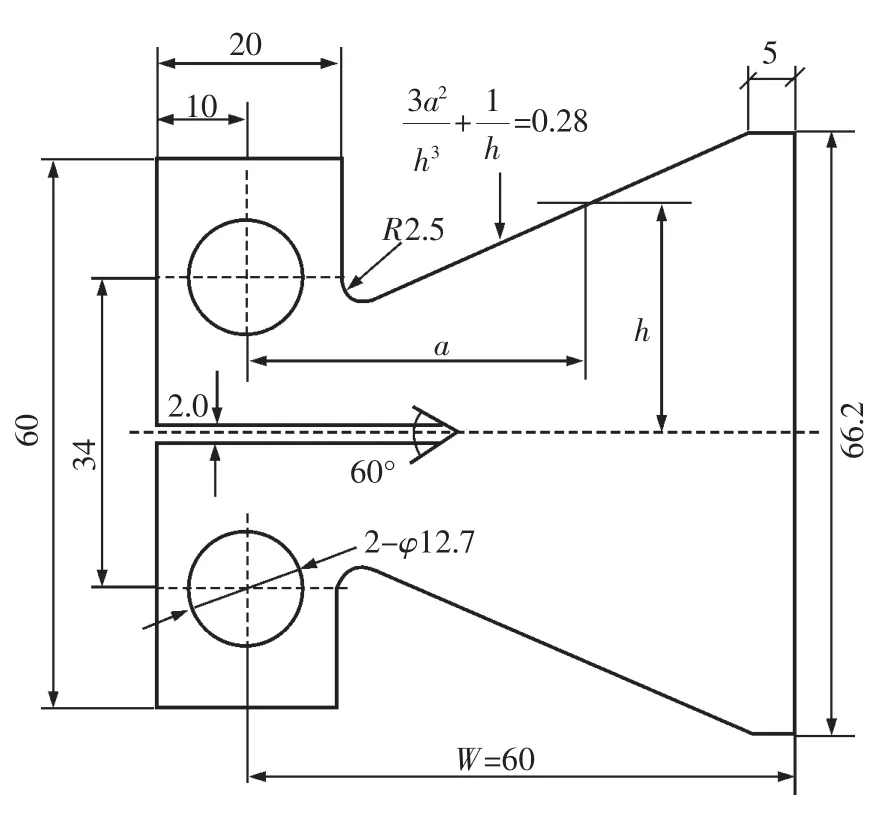
图2 CDCB试样几何形状和尺寸Fig.2 Geometry of the CDCB specimen
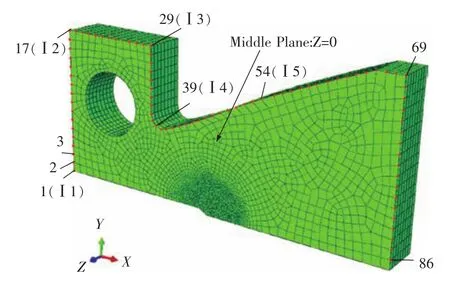
图3 有限元网格、电流输入点和电位差测量位置Fig.3 Finite elementmesh,current injection points and potential difference probe positions
试样接线点布局包括电流输入点的选择和电位差测量点的选择2方面。考虑5种电流输入位置,如图3所示,均位于垂直于试样厚度方向(Z方向)的中间平面上,电流输入点为 I1,I2,I3,I4和I5,电流输出点为这些点相对于裂纹面的对称点。在载荷模块中,向电流输入点加载集中电流,在边界条件中,设置试样韧带为零电势,模拟恒定电流通过试样。在分析步模块中,共建立13个分析步,通过在每个分析步中改变零电势面沿X方向的长度来模拟裂纹长度的增长。取初始裂纹长度a0=0.4W,从初始裂纹开始按裂纹长度a每增加0.5 mm计算1次,通过13步计算获得所需要的全部计算结果。为了验证仿真计算的正确性,对公式(2)所适用的情况进行了建模分析,计算结果与解析解误差在0.1%以内,这说明所用的仿真计算方法具有足够精度。
电位差测量点的选择有多种可能,如图3所示,考查的电位差测点与电流输入点位于同一平面上,在此平面上取试样边界上所有单元结点以及其相对于裂纹面的对称点作为电位差测量点,共86种电位差测量点布局方案。在图3的半模型中,从试样缺口嘴部开始沿逆时针方向将所有测点依次标记为1,2,…,86,以此来表示选定的电位差测量位置。
3 分析和讨论
图4给出了试样电位场的一个示例(电流从I2点输入,a/W=0.45),比较图 4(a)和图 4(b)可以看出,试样前表面的电位分布与垂直于Z轴的中间纵切面的电位分布差别不大。根据计算结果数据,试样在各纵切面内的电势分布在电流加载点附近差别较大,但在离电流加载点稍远处差别非常小,这说明在中间纵切面讨论电流加载点和电位差测量点是合宜的。
3. 1 信号灵敏度
电流从I1点和I2点输入时6个测点的电位差U与无量纲化裂纹长度a/W关系曲线如图5所示。从图中可以看出,电位差信号的量级为微伏级,各测点差别较大,电位差随裂纹长度的变化曲线非常平坦,信号灵敏度低。
图6给出了电流从I1,I4和I5输入时10个测点的电位差增量ΔU与无量纲化裂纹长度a/W关系曲线,从图中可见,ΔU-a/W曲线近似呈线性关系,测点1,9,17,23,29,33和39的曲线几乎重合。根据图3,这些测点均位于试样缺口一侧。这说明当测点位于试样缺口侧时,电位差测点位置对信号灵敏度影响不大。比较图 6(a)、(b)和(c)可见,电流输入位置的不同对各测点灵敏度的相对关系几乎没有影响。

图4 试样电位场计算结果(μV)Fig.4 Calculation results of potential field in the specimen
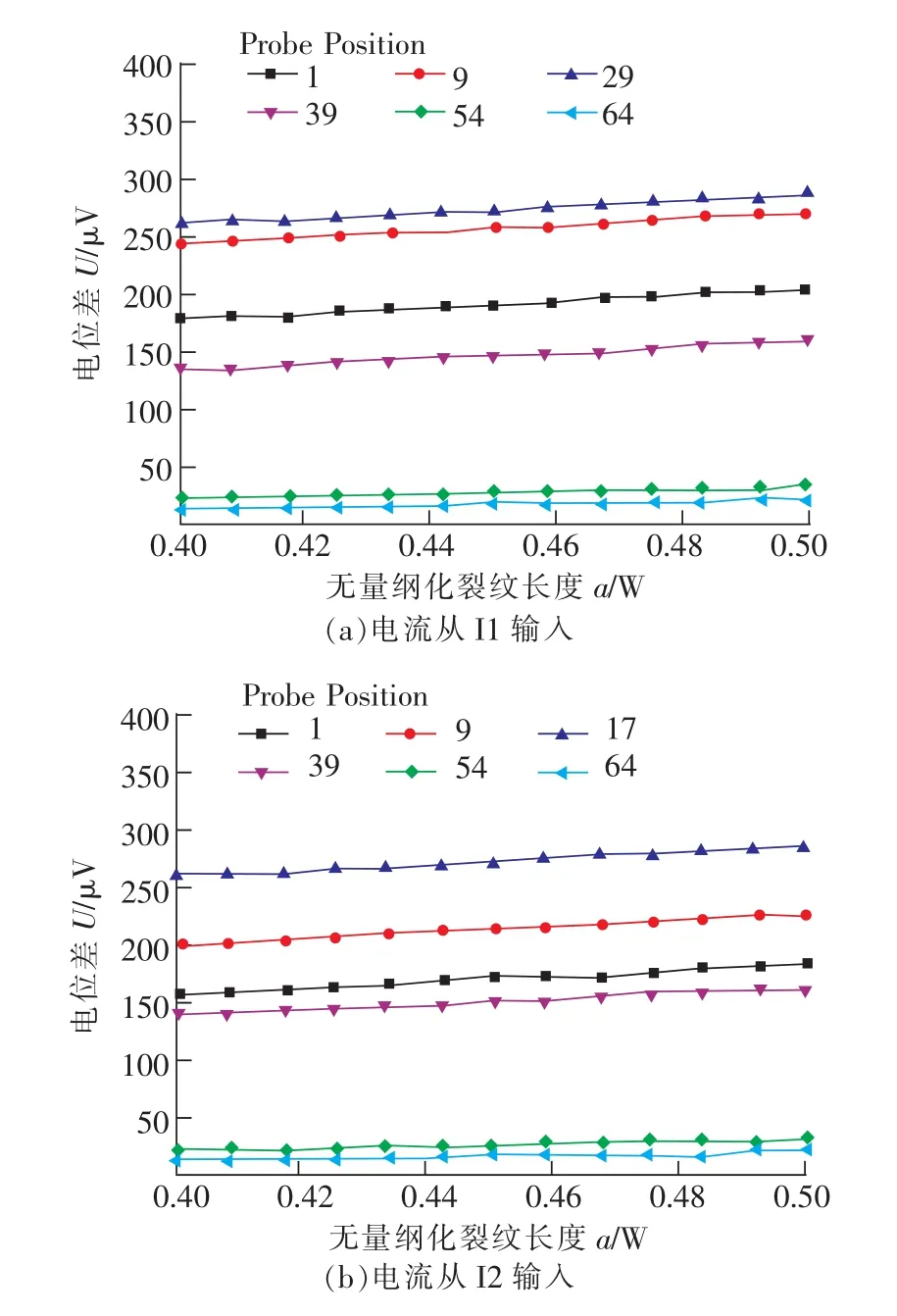
图5 电流从I1点和I2点输入时各测点的U-a/W曲线Fig.5 U-a/W curves ofmeasurement points when current inputs from I1 and I2
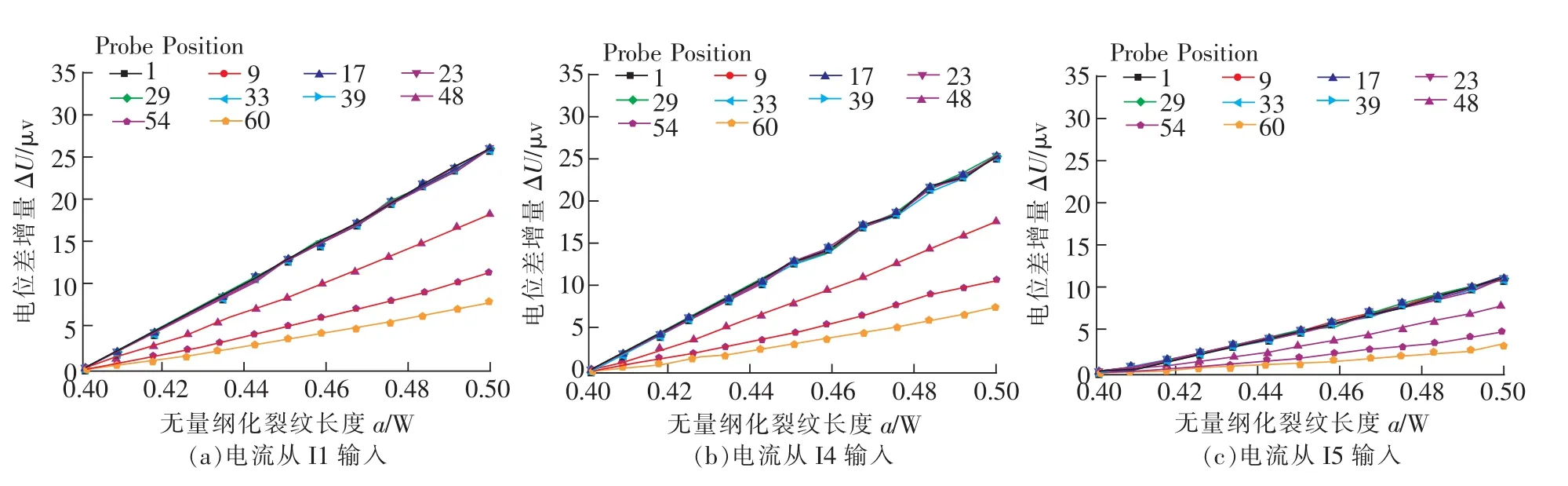
图6 不同电流输入点的ΔU-a/W曲线Fig.6 ΔU-a/W curves of various current input points
为了进一步比较所有测点的灵敏度相对关系,图7给出了裂纹长度增量Δa=0.05 W和Δa=0.1W时5种电流输入位置下所有测点的电位差增量ΔU。从图中可以看出,在测点1(试样缺口嘴处)ΔU最大,随后单调降低。因此,当电位差测点位于试样缺口嘴处时,信号灵敏度最大。从图7还可以看出,电流从 I1,I2,I3,I4输入时的曲线几乎重合,而从I5输入时ΔU显著降低。根据图3,电流输入位置I1,I2,I3,I4均位于试样缺口一侧。这说明电流输入位置位于试样缺口侧时,其对信号灵敏度的绝对大小几乎没有影响,而当电流输入点远离试样缺口侧时,各测点灵敏度显著降低。
3. 2 信号幅度
由于表征裂纹长度的电位差信号非常微小,信号幅度的大小也是选取接线点布局的重要依据。图8给出了电位差测点位于缺口嘴处时5种不同电流输入位置下的U-a/W曲线。从图中可以看出,从I1点输入电流可以获得最大的信号幅度,这时电位差测点和电流加载点重合。为了比较试样边界上所有测点的信号幅度,图9给出了a/W=0.45时5种不同电流输入位置下的电位差与测量位置关系曲线。从图中可见,电流输入点I1,I2和I3对应的信号幅度较大,而I4和I5对应的信号幅度较小。可见为了获得足够的信号幅度,电流输入点应选在试样缺口左侧边界或上侧直线边界部分。
当电流输入位置一定时,信号幅度最大值均出现在电位差测点与电流加载点重合时,这时可以只使用一对导线同时完成电流加载和电位差测量,但实际中通常不采用这种方案,这是因为在这种情况下,电位差信号对导线与试样之间的接触电阻非常敏感,导致测试误差大大增加[30]。从图9还可以看出,信号幅度的最小值与电流输入位置关系不大,均出现在试样右侧。
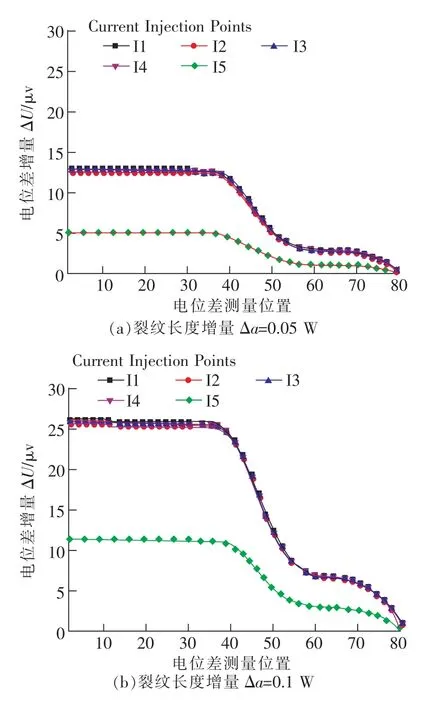
图7 不同裂纹长度增量的电位差增量Fig.7 Increment of potential difference in different crack length increments
3. 3 电位差测量点位置误差影响
在DCPD技术中,导线通常由人工操作点焊机焊接到被测试样上,焊点位置难免会存在误差。电位差测点的位置偏差可分为沿试样边界(X-Y平面内)方向和沿厚度方向(Z方向)2个方面。
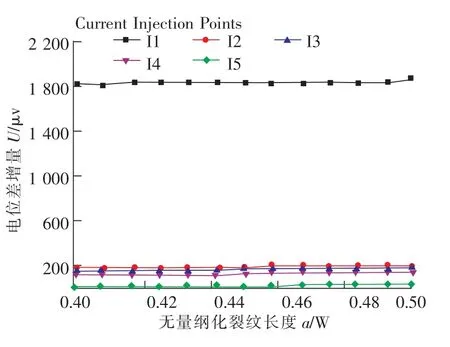
图8 缺口嘴处的U-a/W曲线Fig.8 U-a/W curves at notch mouth
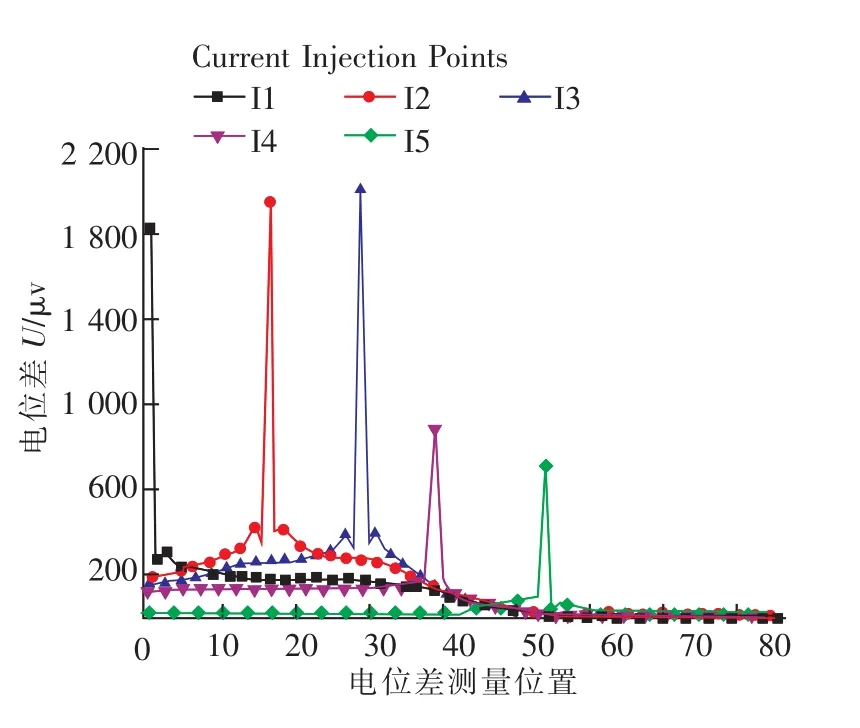
图9 所有测量位置的电位差,a/W=0.45Fig.9 Potential difference at all measurement positions,a/W=0.45
在沿试样边界方向上,从图9可以看出,随着电位差测点远离电流输入点,信号幅度快速衰减,然后趋于平缓。因此,当电位差测量点位于电流输入点附近时,电位差随测点位置变化较大,而当电位差测量点远离电流输入点时,测点电位差受测点位置变化影响不大。图10给出了a/W=0.45时所有测点电位差对测点位置的敏感度S(单位毫米的电位差变化量),从图中可见,只要电位差测点距离电流输入点较远(约0.12W以上),位置误差的影响可以忽略。根据图9和图10也可以推断,焊点大小对试样电位场的影响是存在的,但在距离焊点较远的地方影响可以忽略。
在沿厚度方向方面,图11给出了电流从I1和I2输入时试样中间平面和前表面上沿试样边界各测点的电位差。可见,在靠近电流输入点处,中间平面上和前表面上各点的电位差相差较大,但在稍微远离电流输入点处(距离约0.12 W以上),二者相差非常微小。因此,只要电位差测量点与电流输入点距离较远,在厚度方向上电位差测点位置误差的影响可以忽略。
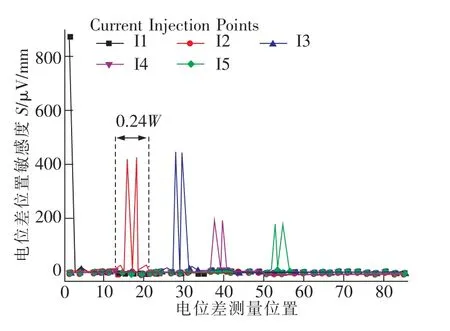
图10 所有测量位置的电位差位置敏感度,a/W=0.45Fig.10 Potential difference position sensitivity for allmeasurement positions,a/W=0.45
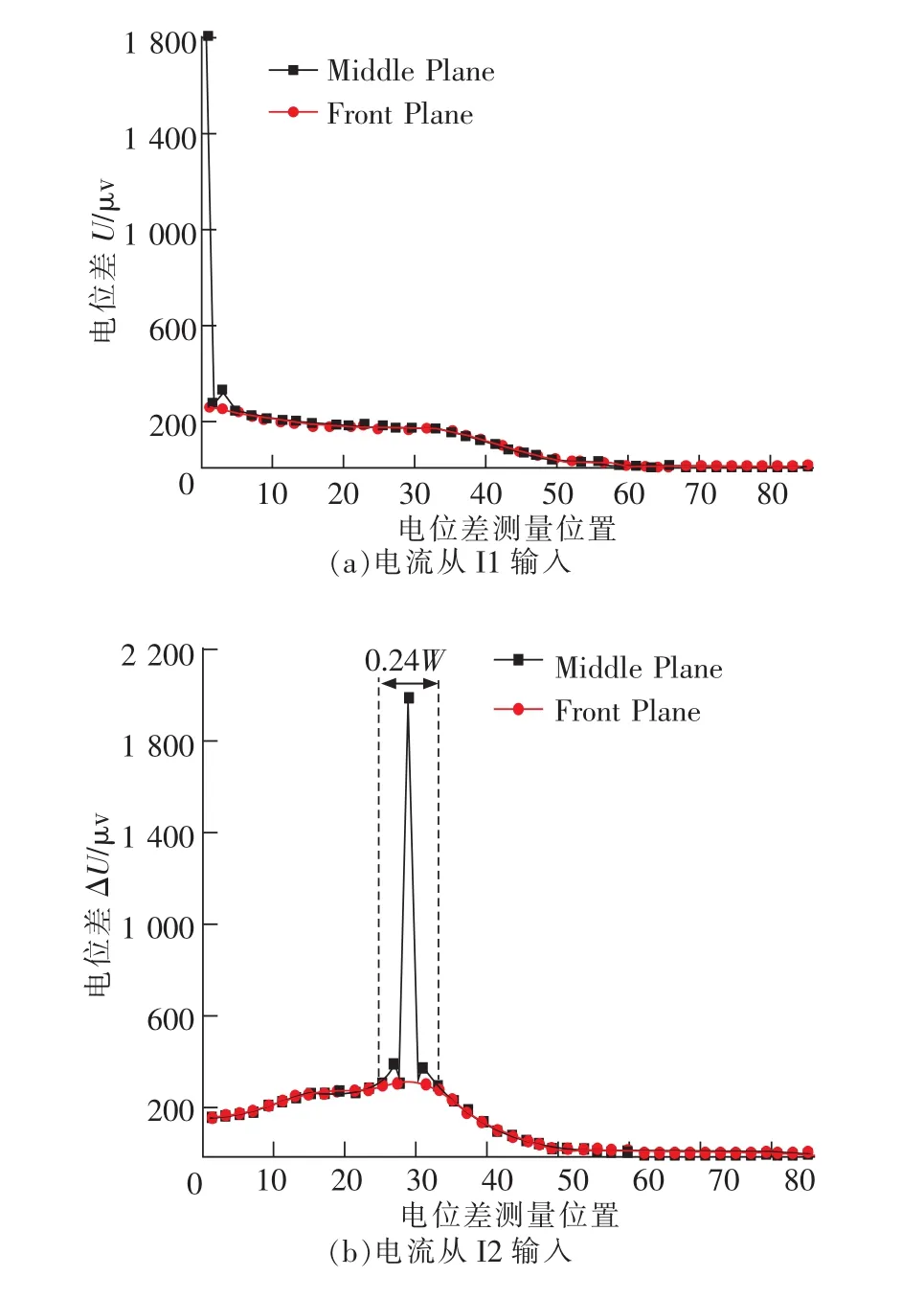
图11 不同纵切面内边界上所有测量点的电位,a/W=0.45Fig.11 Potentials of allmeasuring points on the boundary of different longitudinal sections,a/W=0.45
4 结 论
1)DCPD法裂纹扩展监测中电位差测点位置和电流输入位置均对信号灵敏度有影响,当电流输入位置位于试样缺口侧时,电位差信号的灵敏度大小主要取决于电位差测点位置。试样边界上各电位差测点的灵敏度相对大小关系与电流输入位置无关,电位差测点选在试样缺口侧时可获得较高的信号灵敏度,选在缺口嘴处时信号灵敏度最大;
2)电流输入点位置的变化对试样电位场分布有相当的影响。当电流输入点与电位差测点重合时,可以获得最大的信号幅度,但是,这种情况下电位差信号对测点位置误差非常敏感。为了避免测点位置误差的影响,电位差测点应选在距离电流输入点较远处,具体距离可用有限元法确定;
3)利用ABAQUS软件建立了CDCB试样的三维有限元模型,对试样的接线点布局方案进行了寻优分析,不但给出了合理的试样接线点布局,提出的寻优依据和分析方法也可应用于其他类型试样,为进一步研究环境温度波动、试样局部应变、裂纹闭合效应等因素对测试精度的影响奠定了基础。
