基于Sobel边缘检测的圆周Harris角点检测算法
2019-04-04董立红彭业勋符立梅
董立红,彭业勋,符立梅
(西安科技大学计算机科学与技术学院,陕西西安710054)
0 引 言
图像亮度发生剧烈变化,亦或者图像边缘曲线上曲率的极大值点[1],称之为角点。角点是在图像处理中的一个重要特征,它主要运用到运动目标识别和跟踪、图像匹配等计算机视觉领域。角点检测的精确度,直接决定了识别、跟踪及匹配结果的好坏,因此角点检测是计算机视觉处理中十分重要的环节。
Harris算法是一种传统的角点检测算法,它是在Moravec算法的基础上,由Harris C和Stephens M两人在1988年改进发展而来的。Harris角点检测存在一些不足,如需人工设置阈值[2],存在伪角点、角点簇,角点定位不精确以及检测效率低下。针对Harris角点的信息丢失和位置偏移问题,2009年毛雁明、兰美辉等人提出了双阈值的想法,根据2次非极大值抑制,结合一定区域内有一个角点的方法,确定角点,但是并没有解决人工阈值选取[3]。对于定位不精确的问题,2013年张晶等提出B样条函数来代替传统算法算法中的高斯平滑函数,进而改进了窗口大小选择困难的问题,提高了定位精度[4]。2015年龚平、刘相滨提出了运用像素点响应值进行曲线拟合的方法,根据峰值来确定角点,解决了人工阈值选取带来的角点分布不均现象[5]。2015年邹志远等人提出了一种自适应阈值的方法,对人工选取阈值得到的改善,从而避免人工选取阈值造成的角点分布不合理的现象[6]。2016年赵萌等人提出了一种高斯函数参数自适应的Harris角点检测算法[7],解决了高斯函数参数选取的不确定性影响。由于人工设置阈值易产生角点簇的现象,2017年张见双等人提出了一种改进的算法[8],通过图像分块处理,并在每个图像块中进行自适应阈值设置[9-10]的方法,改善了角点簇现象。
针对Harris算法的不足,上述提到的不同方法都取得了一定的成效,但均不同程度地降低了检测算法的运算效率,如何在提高检测算法效率的同时,降低误检测的率成为文中的研究方向。文中提出运用Sobel边缘检测[11-12]来备选角点来提高检测`效率;在进行非极大值抑制时,文中把传统的矩形模板改为圆周模板,该模板具有旋转不变性,大大改善了图像角点的检测精度,最后采用邻域内临近角点剔除[13-14]的方法,排除角点簇,进一步提高检测的精确度。
1 Harris角点检测
1. 1 Harris角点检测原理
Harris算法是一种传统的角点检测算法,角点就是二维图像灰度值的突变或者图像边缘的交线的轮廓点,在对图像I(x,y)进行移动时,当移动距离是(Δx,Δy),可根据自相关函数给出公式

式中 (x,y)为中心图像;w(x,y)为加权函数,一般为高斯加权函数。
一般我们把上式中 I(u+Δx,v+Δy)进行一阶的泰勒展开

式中 Ix,Iy分别为I(x,y)在 x轴方向上和y轴方向上的一阶偏导数,由以上(2)代入式(1)可得

可以简单理解为图像发生平移后,其自相关函数变成了近似的二项式函数

式中

二次函数就是一个椭圆函数,它的扁率和尺寸是由矩阵M(x,y)的特征值决定的,假设它的特征值[15-16]分别为 λ1,λ2,当它的大小可分为 3种情况
1)当2个特征值差距很大时,即λ1≫λ2亦或者λ2≫λ1,表明自相关系数在一个方向上大,在其他方向上小,是图像中的一条直线;
2)2个特征值相似且比较小,表明其在各个方向上的自相关系数都小,是图像的平面区域;
3)2个特征值都比较大,而且近似,自相关函数在所有的方向上都增大,即为角点。
但是在进行读图像的角点检测时,特征值的计算量十分的大,一般运用特征点的响应函数[17-18]CRF来计算。

式中 det M为M的行列式;trace M为矩阵M的迹;CRF为角点的响应函数;k为常数,一般取k∈(0. 04,0. 06)。响应函数 CRF值大于预先设定的阈值,且为局部最大值,我们称这个点为候选角点。
1. 2 Harris算法步骤及不足
通过对Harris角点检测的理解分析,可将其过程分为3部分
1)首先应该求出矩阵M以及分别在x轴(水平方向)、y轴(垂直方向)上的梯度;
2)对图像做高斯滤波[19-20]处理,求出新的矩阵M;
3)计算出每个Harris角点的响应值 CRF,对局部邻域进行非极大值抑制,与给定阈值进行比较,大于阈值的角点设置为角点。
Harris角点检测有许多不足之处,比如人工设置阈值、抗躁性差、易产生角点簇、伪角点,及其运算时间长等缺点。
2 圆周Harris角点检测
文中提出的圆周Harris角点检测算法,首先采用Sobel边缘检测的方法来获取备选角点,以此来提高检测效率并剔除部分伪角点;随后,对于圆周模板的旋转不变性[21-22],提出了圆周模板来代替传统的矩形模板,提高了角点的检测精度;最后对于角点簇,文中采用邻近角点剔除的方法,剔除伪角点和角点簇,进一步提高了算法的检测精度。
2. 1 备选角点的选取
通过对角点定义易得,角点一定在图像的边缘上,因此文中采用Sobel边缘检测算法对图像进行边缘检测,设置一个阈值(文中Sobel中阈值为150),当某一像素的梯度值大于阈值时,文中认为它就是边缘,否则认为其不是边缘,把检测到的边缘当做备选角点,从而为后来Harris角点检测减少了运行时间。文中采用积木图作为实验原图(如图1(a)所示),通过 Sobel边缘算法进行备选角点,由于只在积木的边缘点进行检测故得到5 141个角点(如图1(b)所示)。原图积木图为256*256=65 536个像素点,备选角点远小于原积木的像素点个数,运行个数约为原来的7.84%,极大地减少了运行时间。
Sobel算子包含2组(横向和纵向)3*3的矩阵,它们分别在x方向和y方向与原图像进行平面卷积,为了得出x方向及y方向的亮度差分近似值。假设我们把A作为我们的原始图像,Gx及Gy分别为方向x及方向y的图像,其公式如下

计算每一个像素的梯度大小,可以用Gx和Gy近似值可得公式如下

当梯度G大于给定阈值时(文中选取阈值为150),文中认为该点就是边缘检测点,即备选角点。
2. 2 圆周非极大值抑制窗口
Harris角点检测的灰度相关矩阵为

角点检测判别式为

图片I经过旋转、平移、缩放后,I′=h·S·I+β,其中G(σ)为卷积函数;h为标量,表明缩放的比例大小;S为旋转矩阵;β为偏移量。变换后的坐标变换关系为

一阶导数关系

式中Iu,Iv为图像在u和v方向的偏导数。
将矩阵窗函数变成一维向量,利用相关矩阵表示相关矩阵M,在原图像中,Iu加权后利用一维向量表示为a,Iv加权后用一维向量表示为b,同理,Iu′,Iv′变换后用 a′,b′来表示。公式如下所示


原图像的相关矩阵为

带入可得

由于变换后的灰度相关性为

故变换后的灰度相关矩阵为
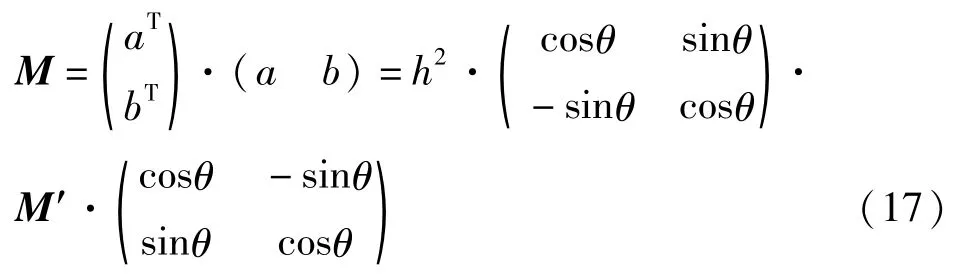
当h=1时,即发生平移和旋转时,变换前后的矩阵是相似的,故其行列式det和迹trace不发生改变,所以旋转和平移后判别式没有影响。
当h≠1时,即缩放变换,变换后的矩阵不相似,故Harris角点检测不具有尺度不变性。
在一般的Harris检测中,一般选用3*3的模板(如图2(a)所示)进行与周围的8邻域进行比较角点响应值,只有当8邻域响应值均小于中心点时,认为此时的中心点是该模板中的极大值点。在传统的算法中,由于非极大值抑制窗口为矩形,当图像发生旋转时,非极大值抑制窗口内的值将会发生变化,对于检测的角点的非极大值抑制也会随之改变(如图2(b)所示),因此文中提出圆周非极大值抑制窗口方法(如图2(c)所示),通过圆周上像素点与中心点的比较来确定角点,当中心点的角点响应值大于圆周上所有的值时,认为此时的中心点就是角点。由于圆周上各点到中心点距离相等,当图像发生旋转时,圆周上的点不会发生变化,进而模板内的非极大值抑制也不会改变(如图2(d)所示),因此文中提出的圆周非极大值抑制窗口算法具有旋转不变性。

图1 实验结果对比Fig.1 Comparison of experimental results
2. 3 剔除部分伪角点
在进行了角点的预筛选以及非极大值抑制之后,局部会有一些角点簇和伪角点出现,即在一定的领域内可能出现2个或者多个角点,这对于一些后续处理可能导致不准确,比如图像匹配,角点簇可能导致匹配概率的明显增加,因此文中应该消除这种现象的出现,文中采用邻近角点的剔除,即在一定的局部范围内,只允许一个非极大值的出现,当在局部范围内,出现2个或者以上的角点,选取非极大值最大的作为角点,排除其他的角点,文中采用5*5的模板。
3 实验结果和分析
为了更好地验证文中算法的准确度,选择积木图像作为实验原图像(如图1(a)所示)。参数分别选取 p=0. 010,p=0. 005,半径 R=2,将圆周窗口算法与传统算法进行对比实验,实验结果如图1所示。
3. 1 算法时间和准确度对比
阈值选取为p·Max,将传统算法和文中算法进行比较,算法效率见表1,算法准确度(正确角点数/(正确角点数+伪角点数+漏检角点数数))见表2.

图2 传统算法和圆周算法Fig.2 Traditional and circumferential algorithms
由实验结果可知,原始Harris角点检测算法的漏检角点比较多,运行时间比较长,提出的圆周角点检测算法,漏检角点明显减少,以p=0.010为例,准确度由传统算法的61.19%提高到76.92%,且通过采用Sobel边缘检测角点备选方法,大大提高了算法的检测效率,平均时间从原来的0.769 583 s降低到0.238 220 s,约为传统算法的31%.
3. 2 旋转不变性对比
将图1(a)图像旋转45°角后作为实验图像,采用“错准比”((误检数+漏检数)/准确数)对文中圆周检测算法及传统算法进行结果比较,实验结果如图3所示,错准比比值越大,检测效果越差,见表3.

表1 算法运行时间(单位秒)对比结果Tab le 1 Com parison of algorithm running time(in seconds)

表2 算法精确度对比结果Table 2 Algorithm accuracy comparison result
由表3可知,对于旋转后图像,提出的圆周检测算法伪角点数得到了明显的减少,漏检角点也有所改善,因此文中算法的错准比明显低于传统算法,尤其当p=0.010时,错准比由传统算法的45/22下降至30/22.由此可见,提出的圆周检测算法具有较强的旋转不变性。

表3 实验对比结果(旋转45°)Table 3 Experimental comparison results(rotation 45°)

图3 旋转不变形实验对比Fig.3 Rotation without deformation experiment comparison
3. 3 抗噪性对比
对原始图像加入φ=0,δ=0. 005的高斯白噪声[20],对传统算法和文中算法进行试验对比。
如图4所示对比传统Harris角点检测算法,文中算法大大改善了角点簇和伪角点的影响,因此文中算法具有较强的抗噪性。
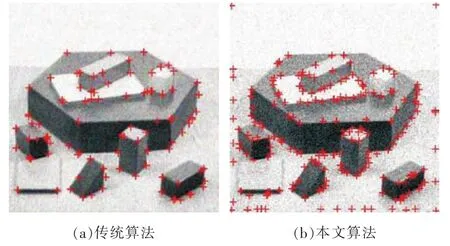
图4 加入噪音后实验对比Fig.4 Experimental comparison after adding noise
4 结 论
1)实验结果表明文中改进算法相较于传统算法,检测精度提高了约10.52%,检测效率提高了约69.05%;
2)提出的改进算法相较于传统算法,具有旋转不变性及较强的抗噪性。由于本文算法阈值的选择仍为人工选取,适用性与适应度不够高,是未来研究的重点。
