例谈多面体外接球半径的常见求法
2019-04-04湖北省荆州市沙市第五中学张胜言
数学大世界 2019年5期
湖北省荆州市沙市第五中学 张胜言
方法:首先构造简单的几何体,如长方体、正方体、三棱柱等,易作出这些简单几何体的外接球,从而求解。
定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
一、长方体、正方体外接球的半径
1.长方体:因为长方体外接球半径是体对角线长的一半,设长方体长、宽、高分别为a,b,c,外接球半径为r,则(如图1)。

图1

图2
二、三棱柱外接球半径
1.底面是直角三角形的直三棱柱
把三棱柱补成长方体,易求(如图3)。设底面三角形两直角边长分别为a,b,直三棱柱高为c,则外接球半径为r,则
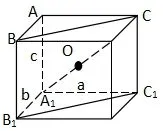
图3
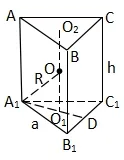
图4
2.正三棱柱
如图4,正三棱柱球心O在两底面中心O1,O2的中点处,设底面边长为a,高为h,外接球半径为r,构造Rt△A1OO1,则
三、三棱锥外接球半径
1.三条棱互相垂直的三棱锥
如图5,把它补成以这三条互相垂直的棱为长、宽、高的长方体,易求。
2.三组相对棱分别相等的三棱锥
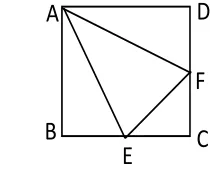
图7
3.正四面体
例题1 如图7,正方形ABCD的边长为4,点E,F分别是BC,CD的中点,沿AE,EF,FA折成一个三棱锥B-AEF(使点B,C,D重合于点B),则三棱锥B-AEF的外接球半径为________。
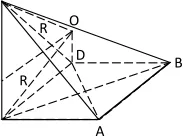
图8
