高三文科求解几何体体积复习策略
2019-04-04云大附中星耀校区刘云英
云大附中星耀校区 刘云英
三维空间是人类生存的现实空间,认识空间图形,培养和发展学生的空间想象能力、推理论证能力及运算能力是高中立体几何学习的基本要求。教材从对简单几何体的认识出发,研究空间中点、线、面的位置关系,并对几何体的相关量进行计算。针对教材的设计意图和教学目标,文科数学高考命题中空间平行垂直的性质及判断,几何体体积的计算成了必考的内容。因而,高三复习阶段,空间平行、垂直关系的快速证明,几何体体积及距离的准确计算便成了复习时必须达成的教学目标。
文科学生的空间能力较弱,往往凭直觉去解决问题,求值耗时长,得分低。因而,带领学生构建系统的求值思路,快速找到求值路子,是高三复习的教学重点及难点。在此,我们将系统分析几何体求体积或距离的问题。
一、难点
求空间几何体的体积,常用方法有:割补法、直接法、等体积法。割补法对空间想象力差的文科生来说,对一个几何体进行割补并不是他们的强项;直接法,高考命题中极少出现能直接找到所给底面高的情况,问题的设置难点在找几何体的高,往往需要“曲线救国”,通过转换几何体的顶点及底面利用等体积法来完成。在此我们探讨用等体积法求解空间几何体体积的常规思路。
二、思路及方法
1.底面的确定方法:既然待求几何体顶点到底面的垂线段难找,那“曲线救国”必须选取几何体中容易找垂线的面作底。确定底时注意关注以下两点:(1)关注已知或已证的平面,利用已知条件中或已证过垂直关系的平面作底,几何体的高就是面的垂线,或选取有平行关系的面作底;(2)关注几何体中站位较有利的平面,比如平放或竖直放置的面作底,这样的平面更容易找到垂线。
2.在确定所需底面时,会涉及点的灵活转换,以便构建理想的底面。具体点的转换主要有两个依据:
(1)平面的平行线上所有点到平面的距离相等。
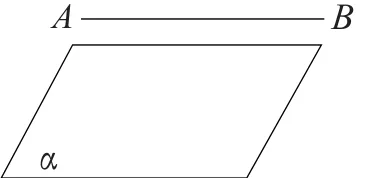
(2)中点转化:

三、例题分析
【分析】(1)略
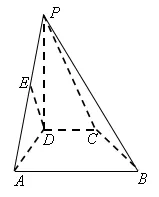
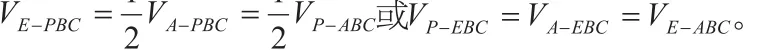
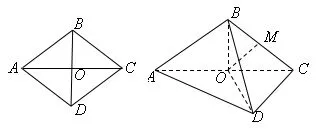
【分析】(1)略
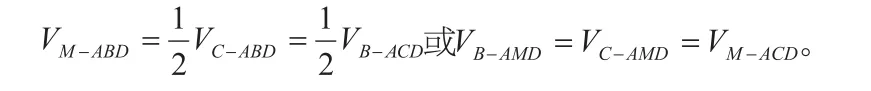
总之,求几何体的体积时,若能关注到题设或推证过程中涉及的平面及几何体中位置较特殊的平面,把它们选作底面将可用等体积法快速解决求体积问题。当然,用等体积法的前提是求三棱锥的体积,若所求问题是多于四个面的几何体,则需在多面体中选取较有优势的四个不共面点构成三棱锥解决问题。
