摒弃 传承 创新 反思
——以一年级下册《求两个数量相差多少》为例谈解决问题教学
2019-04-04浙江省杭州市育才京杭小学莫慧萍
浙江省杭州市育才京杭小学 莫慧萍
新课改把传统的应用题教学重新进行了定位与包装,将“应用题教学”更名为“解决问题”,文字变化的背后是一种新的教学理念的诞生。根据应用题教学在新教材中的编排特点,在教学中要做相应的调整, 既不能沿用过去按类型、套算法的方法教,也不能全盘否定我们传统的应用题教学。那么怎么教呢?“求两个数量相差多少”是低段年级一节比较典型的解决问题。笔者就想以此为例,来谈谈教材定位与教学设计上如何尊重学生实际,走出传统束缚,开创教学的新天地。
一、“求两个数量相差多少”的理解与定位
传统“求两个数量相差多少”应用题教学中非常关注学生对解题思考过程的完整表达,讲求语言的条理性和逻辑性,非常关注数量关系的理解和建构。新课程下的低段解决问题教学需不需要学生完整地表述思考过程?需不需要帮助学生建立清晰的数学模型?等等都需要进一步探讨,笔者认为:
1.“求两个数量相差多少”其本质是一一对应思想与方法的实际应用
小学数学教学中主要利用虚线、实线、箭头等图形将元素与元素、实物与实物、数与算式、量与量联系起来,渗透对应思想。学生在一年级上册学习“比一比”的过程中,通过画虚线的方法,将一一对应的思想进行了具化,积累了比较丰富的数学学习经验和大量的表象。“求两个数量相差多少”的认知基础是一上年级的“比一比”,其本质就是一一对应思想方法的实际应用。当学生能用画虚线的方法掌握一一对应思想方法的同时,也就对“减去同样多的部分”这一难点问题了解比较深刻,从而解决并掌握了求相差关系的问题。
2.“求两个数量相差多少”应该突出数学模型的建构过程
数学学习强调从学生已有的生活经验出发, 让学生亲身经历将实际问题抽象成数学模型的过程。所以有人说“数学是一门模式化的科学。”数学模型是新课程小学数学的核心概念,它的建立是学生形成数学思想、解决数学问题的基本任务。但是我们许多教师始终不明白数学模型究竟是怎么回事,更谈不上有目的、有计划地帮助学生建立数学模型。因此,让学生建构一定的数学模型是非常重要的。“求两个数量相差多少”作为小学阶段解决问题的第一课,应该根据学生的年龄特征和认知水平,以足够的表象做支撑,让学生来经历、体验这种数学建模的过程,实现有效地建模。
鉴于以上分析,笔者认为求相差关系的问题的目标着力在两个关键词:“经历过程”,即通过具体操作和合情推理,经历发现求两个数相差多少用减法计算的过程;“初步理解”,即通过排一排、比一比等活动体会一一对应的数学思想,初步理解求两个数相差多少的实际问题的结构和数量关系。
二、“求两个数量相差多少”的教学策略
一年级的学生学习数学的过程中,形象思维占主导,他们主要借助观察、操作等直观的方式进行学习活动。通过丰富的表象积累,从具体到抽象,逐步构建出较为清晰的数学模型。因此,要找到有效的具象载体,借助表象,促进学生建模。
(一)千朵万朵梨花开——注重丰富的表象积累,促进模型建构
数学模型关注的对象是许多具有共同普适性的一类事物,因此,教师首先要给学生提供丰富的感性材料,多侧面、多维度、全方面感知这类事物的特征或数量相依关系,为数学模型的准确构建提供可能。教学时,笔者通过摆一摆、画一画、说一说、猜一猜等活动促进学生进行模型的建构。
【教学片段】
1.摆一摆,初步感知
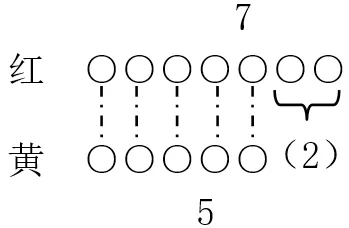
(1)师:老师在信封中放了一些红圆片和黄圆片,倒出来看看谁多谁少?老师有个要求:要让其他小朋友们一下子就可以看出红圆比黄圆多几个?想一想,怎么摆?
学生摆一摆,教师巡视,选择学生不同的摆法贴在黑板上。
(2)师:比较一下,哪种摆法好?
重点讲解一一对应摆的方法:一个对着一个摆,指名画上对应线。
师:红圆片比黄圆片多几个,还可以怎么说?(学生:黄圆比红圆少几个?)
师小结:这样就相当于把红圆片分成了两部分:一部分和黄圆片同样多,另一部分就是比黄圆片多的。算式你会列吗?指名列式:7-5=2。
(3)课件演示,清晰思路
师:看大屏幕,我们一起再来摆一摆。
师: 7-5=2,7、5和2各表示什么意思?学生:7个红圆片;5个黄圆片。师追问:5除了表示5个黄圆片,还表示5个——?学生:5个红圆片;2表示红圆片比黄圆片多2个。
师:谁能完整地说说7-5=2表示什么意思?
看着图,同桌小声地说说这个算式表示什么意思?
(4)师小结:红圆片比黄圆片多几个,黄圆片就比红圆片少几个,都是用红圆片的个数减去黄圆片的个数,算式都是7-5=2。
师:怎样使两种圆片一样多?(学生:添上2个黄圆片;去掉2个红圆片)你能用哪个算式表示?(7-5=2)
问:为什么问法不同,计算的方法却相同?学生:都是指红圆片比黄圆片多的2个;都是用红圆片的个数减黄圆片的个数。
师明确:求红圆片比黄圆片多或求黄圆片比红圆片少,或添上几个黄圆片、去掉几个红圆片使它们一样多,意思都是一样的,都是用红圆片的个数减去黄圆片的个数,算式都是7-5=2。
2.画一画,初步理解
(1)8个△,5个○。(师写在黑板上: △8 ○5)
你能提出什么问题?(△比○多几个?○比△少几个?)
师:这两个问题还可以说成:△与○相差几个?
师:请你像黑板上的图这样,画一画。学生完成后挑选一名学生的画作,重点反馈一一对应的比较方法。
师:怎么列式?(板书:8-5=3)说说8-5=3表示什么意思?
(2)同样的方法画一画:5个△,8个○。
(3)比较:画的两个图不一样,为什么算式都是8-5呢?(学生:都是用大的数减去小的数)
师:两个数都是8和5,实际上就是求8比5多几。
【教后评析】
1.在摆图、画图的操作中强化对一一对应思想与方法的感知
一年级的孩子语言能力还比较弱,常常处于一种“只能意会不能言传”的状态。在让学生说一说算式表示的意思时,无论老师如何尽力引导,学生始终无法比较完整地进行表达,因此,笔者认为,教学时,不必刻意地去讲究表述的完整性和条理性,而是要让学生明确“比”的方法,即一一对应,运用摆图、画图的操作活动,从具体形象的图中感知、意会“大数-小数=相差数”这一数量关系,以培养学生处理信息的能力和思维能力。
2.在不同的表述中完善对两数相差多少的实际问题的理解。
利用括线、虚线和问号,简单明了地表明了题意,学生能较快较好地发现“5”既可以表示黄圆片的个数,也表示红圆片中与黄圆片相等的部分,从根源上明白为什么“求两数相差多少”要用减法做。再通过追问:怎样使两种圆片一样多?利用板书操作,学生从直观的图片到抽象的算式,发现:不管是添上还是去掉,都是两者的相差量,对两数相差多少的实际问题的理解变得饱满,学生了解了求两数相差多少同一方法的不同表述形式,及时巩固丰富了减法的含义,帮助他们在以后的解题过程中能由此及彼、由彼及此的思考。
(二)吹尽黄沙始见金——重视具体到抽象跃进过程的组织,构建数学模型
丰富而又感性的数学情景是学生有效建立数学模型,完成数学学习的重要载体,但这只是为学生数学模型的建构提供了可能,如果忽视具体到抽象跃进过程的有效组织,模型的构建也只能是“海市蜃楼式”的美好幻想。因此,教学中,应唤起学生那些蕴涵经验中的非正规的数学知识,经历由数学情景问题到抽象的认识转化过程,实现从生活问题向抽象数学模型的有效过渡。
【教学片段】
1.猜猜,画画
(1)师:现在老师又放进了一些圆片(配合手势),一个对一个地摆好(配合手势),结果发现,红圆片还是比黄圆片多2个。
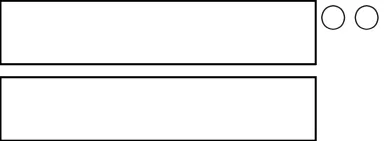
(2)出示算式:8-6=2(个)。
师:根据这个算式猜一猜,盖住了几个红圆片?几个黄圆片?你是怎么知道的?(课件演示)
(3)师:还可能盖住了几个呢?请你在纸上画一画。学生尝试画图。
2.猜猜,写写
(1)请2名学生说盖住了几个,请另外的学生列式:( )-( )=2。
学生:我盖住了7个;众生:9-7=2;学生:我盖住了8个;众生:10-8=2;学生:我盖住了3个,众生:5-3=2……师追问:方法正确,但老师是放进了一些圆片,你认为符合要求吗?
(2)师:答案可以有很多很多,但不管怎样,盖住的红圆片和黄圆片的个数是同样多的。
课件演示:出示虚线框表示盖住的红圆片和黄圆片同样多,再把多的2个红圆片也盖住。
最终出现下图:

(3)师:现在老师直接标上数:12、10,算式怎么列?12-10=2。
【教后评析】
教材一直没有忽视数量关系的教学,只是更加注重学生在解决问题过程中的理解与感悟,提供生活具体情境,让学生从这些纷繁的情境图中提炼出有用的信息,并将这些信息进行思维的加工。学生对这些数学信息进行内在的思维加工过程,就是数学模型的建构过程,而数量关系就是数学模型的骨架。因此,教学时,笔者借助了猜图,逐步建立感性的问题模型,理清解题思路。通过对“盖住了几个”的猜想、画图,让学生在一遍一遍的经历中自主地感知并悟出数量之间的内在关系,对求相差多少获得更本质的理解。这时候学生的认知是深刻的,模型图的构建是充分的、水到渠成的。条状模型图其实是线段图的雏形,它的出现就是把具体数量进行了初步的抽象化,为后续学习线段图奠定了基础。
数学学习不是一件纯粹孤立的事情,每一个知识点总能找到它的逻辑起点。笔者在教学时关注了数学学习的连贯性。二年级下学习“求比一个数多(少)几的数”的问题就是在本课基础上教学的。这种猜测、画图活动就为学生能获得后续学习不竭的动力,进行了有意识的铺垫,这样学生的学习不会显得很苍白、孤立,自觉加以沟通联系。
(三)桃花深处有人家——重视数学思想方法的提炼,突显数学模型的本质
思维方法、思维策略是数学模型存在的灵魂。不管是数学概念的建立,数学规律的发现,数学问题的解决,乃至整个数学“大厦”的构建,核心问题都在于数学思维方法的建立。在构建有效的数学模型的过程中要重视数学思维方法的体验与感悟,提升学生的数学思维能力。
【教学片段】
1.师:把多的数放下面可以吗?
出示:你能看懂图的意思吗?先说说图的意思,出示文字,再列式。
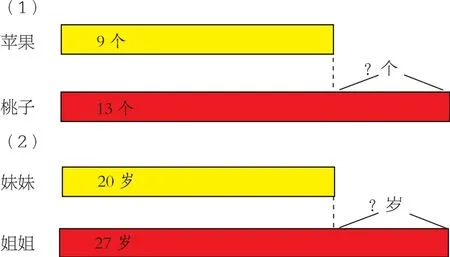
师:把苹果、桃子换成另外的事物,你能提出什么问题?
学生:爸爸比我高多少?桌子比椅子多几张?……
(3)出示问题:书包比铅笔盒贵多少元?
师:想一想,哪个条形表示的是书包?哪个条形表示的是铅笔盒?为什么?
学生:书包贵,铅笔便宜,所以长的那条是书包,短的那条是铅笔。
师:问题在图上是指哪一部分?这样能算了吗?
学生:不能,没有数。
再出示数据,学生列式计算。

2.小结
师:要求谁比谁多(或少)几个,大或小几岁,贵或便宜几元,就是求一个数比另一个数多(少)几,要用减法计算。
【教后评析】
数学学习应该注重数学思想和方法的提炼,这有助于培养学生的抽象思维能力,提升数学学习的能力。因此,在教学时,笔者通过将条状模型图的量与数的变换,从“比多少”拓展到“比轻重”“比年龄”“比价格”等非具象的内容,将各种特征的两个数量的比较问题归结为同一个数学模型,在不断强化数学模型的应用中,拓展对“求两个数量相差多少”的实际问题的数学本质认识。
同时,通过“把苹果、桃子换成另外的事物,你能提出什么问题?”引导学生尝试看图提问。通过对“书包比铅笔盒贵多少元”这一问题的解读,“哪个条形表示的是书包?哪个条形表示的是铅笔盒?为什么?”“问题在图上是指哪一部分?”引导学生进一步清晰问题的数量结构和数量之间的关系,渗透“分析法”这一非常重要的数学解决问题思考方法。因此,重视数学思想和方法的提炼与体验,可以催化数学模型的建构,提升建构的理性高度。
面对解决问题在教材中的编排特点, 我们的教学要做相应调整,既不能沿用过去按类型、套算法的方法教, 也不能全盘否定我们传统的应用题教学,需要我们在新课改的教学中, 不断地继承和批判,不断地奇思和创新,不断地实践和反思。
