识别动力减振镗杆主系统等效参数的数学计算方法

何 苗， 孙蓓蓓

(东南大学 机械工程学院，南京 211189)

深孔镗削加工时镗杆的悬伸量较大，镗杆长径比越大刚度越低，越容易产生切削颤振，所以深孔加工一直是机械加工的难题，也是国内外学者研究的热点。动力减振镗杆是在镗杆内部空腔放置一个有阻尼动力吸振器，可以有效地减少切削颤振，提高加工精度。为了设计减振镗杆，必须建立其动力学模型，需要识别出等效质量和等效刚度，从而把连续体实际结构等效为理想的集中参数模型。所以镗杆主系统的等效参数准确与否，直接关系到镗杆内部的动力吸振器的动力参数设计。

目前，动力减振镗杆的研究大多集中于吸振器参数优化设计[1-5]、颤振抑制机理[6]、吸振器工程实现[7]、动力学特性[8-10]等。Sims针对切削颤振提出一种吸振器的解析调优策略，Miguelez等基于Sims调优策略，给出了镗削过程中最佳调谐频率的新解析表达式，并提出了吸振器频率比和阻尼比的经验拟合表达式，罗红波等利用幅频响应曲线面积最小法来修正全局寻优搜索法求得的设计参数值从而得到一组最优参数值。Henrik等研究了夹紧性能对镗杆动态特性的影响，Sortin等提出一种基于有限元梁和经验的镗刀系统混合动力模型，Moetakef-Imani等给出了镗削过程的动力学仿真方法。

识别动力学模型的等效参数研究不多，大多将等效参数作为已知条件， Miguelez、Rubio等和Houck III等将镗杆模型作为等截面梁进行研究。实际减振镗杆结构(见图1)内部有一长段空腔用于安装动力吸振器，镗杆主系统横截面是不等的。何山等[11]提出的基于正交多项式法的动力吸振器安装点的等效质量识别方法，需要测得动力吸振器安装点的原点频响函数，并用正交多项式进行拟合，对于减振镗杆这类结构较简单的主系统，识别过程较复杂。总之，目前动力减振镗杆等效模型的等效参数识别都是通过实验和仿真的方法，效率低，传统质量感应法识别过程复杂，识别精度低。特别是当镗杆的尺寸、结构、材料等发生改变时，必须重新建模仿真或实验，费时费力，本文提出一种新的识别动力减振镗杆主系统等效参数的计算方法，可以快速计算出镗杆主系统参数，其计算结果比等截面镗杆计算结果更准确，效率和精度相比传统方法提高。

本文将大长径比的镗杆看做悬臂梁，由于横截面不等，目前广泛应用的均质梁的求解公式不再适用，而且等截面悬臂梁的等效质量计算公式也不适用于非自由端等效点的等效质量计算。所以本文根据减振镗杆横截面明显的分段特点，提出了基于欧拉—伯努利梁理论和分段连续条件的方法求解主系统的固有频率和固有振型函数，再根据最大动能不变原则，推导出了主系统等效质量的求解公式，由此可求解出镗杆主系统所有等效参数。数值仿真结果表明，此计算方法比将镗杆作为等截面梁计算更为准确，可准确地计算出动力减振镗杆的主系统参数，从而提高动力减振镗杆设计效率，同时适用于其他不等截面梁等效参数的求解。

1 动力减振镗杆模型

动力减振镗杆的结构简图如图1所示。从图1中可以看出，镗刀杆体、车刀转接头和车刀构成主系统，镗杆内部的振芯、橡胶圈和阻尼油构成了动力吸振器的质量m、刚度k和阻尼c系统，为了设计动力吸振器系统，需要根据吸振器的安装位置对主系统进行动力学等效，从而得到主系统的等效参数。忽略主系统阻尼，动力减振镗杆的等效模型如图2所示。其中，M和K即为主系统的等效质量和等效刚度，m，k和c是吸振器的设计参数。

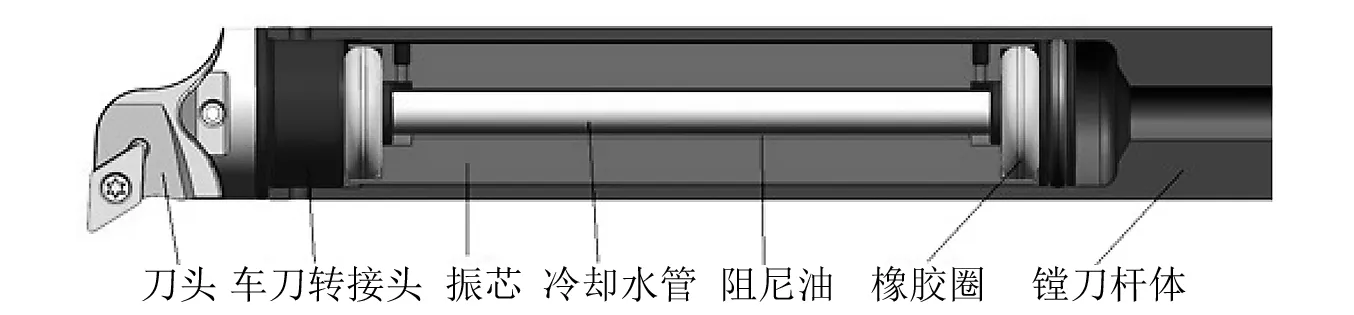
图1 减振镗杆结构简图Fig.1 Dynamic damping boring bar

2Euler-Bernoulli经典梁理论求解镗杆弯曲模态

动力减振镗杆在实际加工中为横向振动，由于其长径比大，所以可以使用Euler-Bernoulli经典梁理论进行计算。根据Euler-Bernoulli梁理论，等截面梁自由振动的运动方程为

图2 动力减振镗杆等效模型Fig.2 Dynamic damping boring bar equivalent model

(1)

求解运动方程式(1)，利用分离变量法，即令y(x,t)=Y(x)T(t)

可得等截面悬臂梁的固有振型函数为

Y(x)=Acos(βx)+Bsin(βx)+
Ccosh(βx)+Dsinh(βx)

(2)

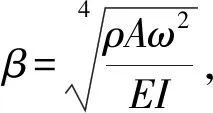
由图1可以看出，镗杆作为非等截面悬臂梁进行计算时，可以根据其横截面不同，分为三段，每段长度用li表示，弯曲刚度和线密度用EIi和ρAi表示(i=1,2,3)。在刀具装夹端建立坐标系，如图3所示，xE为振芯质心位置即吸振器安装位置，也是镗杆主系统的等效点位置。每段连接处的连续条件为位移、转角、弯矩和剪力连续。

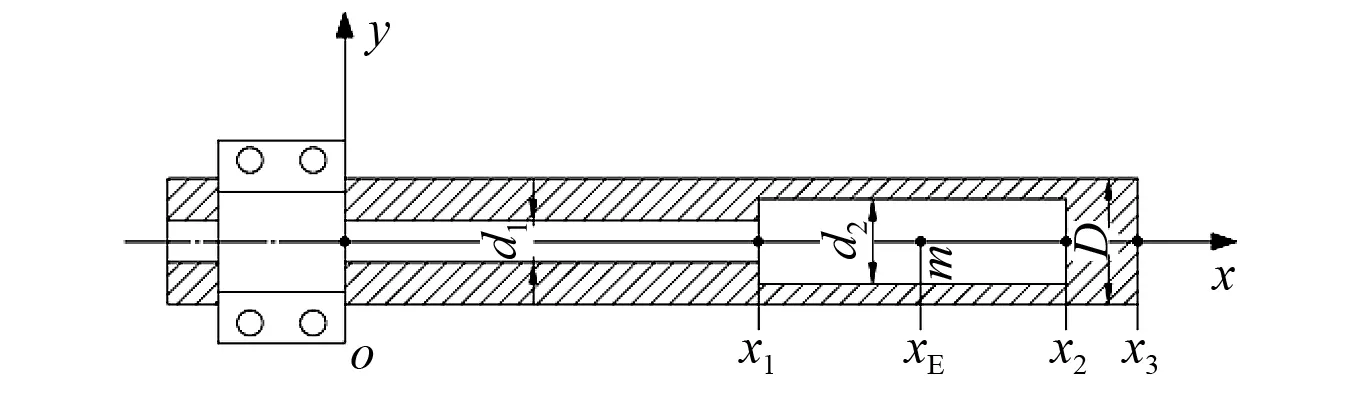
图3 刀杆分段坐标系Fig.3 Boring bar segmented coordinate system

根据Euler-Bernoulli梁理论，减振镗杆主系统的振型函数Y(x)可以分段表示为

(3)

其中，

(4)

将待定系数用矩阵形式表示，即C(i)=[AiBiCiDi]T(i=1,2,3)，则振型函数可以用矩阵形式表示为

Yi(x)=[cos(βiXi) sin(βiXi) cosh(βiXi) sinh(βiXi)]

(5)

根据分段连续条件，即第i段与第i+1段在连接点xi处位移、转角、弯矩和剪力均连续，可得

Yi(xi)=Yi+1(xi)

(6a)

(6b)

(6c)

EIiY‴i(xi)=EIi+1Y‴i+1(xi)

(6d)

将振型函数表达式(5)代入连续条件中(式6(a)～式6(d))，整理可得振型函数的待定常数递推公式为

(7)

其中，矩阵A(i)和Q(i+1)为

(8)

(9)

所以，引入递推系数矩阵Z(i)，可得递推公式为C(i+1)=Z(i)C(i)

(10)

根据悬臂梁固定端和自由端的边界条件，即固定端位移和转角为0，自由端弯矩和剪力为0，可得

(11a)

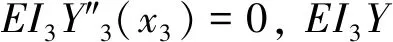
(11b)

将振型函数表达式(5)代入边界条件中(式(11a)和式(11b)，计算可得

则可得

PC(1)=0

(12a)

QC(3)=0

(12b)

由式(10)的待定系数递推公式可得，C(3)=Z(2)Z(1)C(1)，代入式(12b)，可得

QZ(2)Z(1)C(1)=0

(13)

(14)

欲使式(14)有非零解，则其系数矩阵Γ的行列式必等于零，由此可得刀杆横向振动的特征方程为

det(Γ)=0

(15)

特征方程式(15)只有一个未知量，即ω，求解此方程可得ωn(n=1,2,3,…)，对应镗杆主系统的第n阶固有频率。

将所求的固有频率ωn代入线性方程组式(14)中，可求出该阶模态的振型函数待定系数A1，B1，C1，D1，再代入式(10)，得到第二段和第三段的待定系数，从而得到整个刀杆的振型函数。

3 镗杆主系统等效质量和等效刚度的计算

在上一节中，由经典梁理论分段连续原理，已经求出了镗杆横向振动的固有频率和振型函数，根据最大动能等效原则，可计算出镗杆主系统的等效质量。

等效前镗杆最大动能为

(16)

代入上节所求的镗杆的分段连续振型函数，可得

(17)

等效后，镗杆单自由度系统的最大动能为

(18)

式中：xE为吸振器安装位置，即等效点位置。对比等效前后的最大动能表达式(17)和式(18)，等效前后的最大动能保持不变，所以等效后的等效质量为

(19)

等效刚度可由等效质量与固有频率推算得出，所以镗杆主系统的等效刚度为

K=Mω2

(20)

4 减振镗杆等效参数计算实例与结果验证

为验证本文提出的计算方法，以直径32 mm长径比为10的动力减振镗杆为例，该减振镗杆的基本材料参数、结构尺寸参数，如表1所示，其中分段位置和内径参数均参考图3所示的分段坐标系。

表1 动力减振镗杆参数

在该镗杆的刀头处施加扫频激励，测得镗杆的频率响应曲线，如图4所示，由响应曲线可看出，减振镗杆在第一阶频率处振动幅值最大，所以减振考虑镗杆的第一阶模态，即以下计算结果对应镗杆的第一阶模态。

将上节所推导的计算公式，通过MATLAB编程进行计算，计算流程如图5所示。只要输入减振镗杆的基本结构参数，即可计算出该减振镗杆主系统的固有频率、等效质量和等效刚度。输入表1中的镗杆参数，计算结果如表2所示。

根据图4所示的镗杆频率响应曲线可得，扫频实验方法所测得的镗杆固有频率为266.67 Hz，而本文提

出的数学方法计算所得固有频率为268.62 Hz，相比扫频实验结果，相差0.73%，说明本文提出的数学计算方法是准确的。

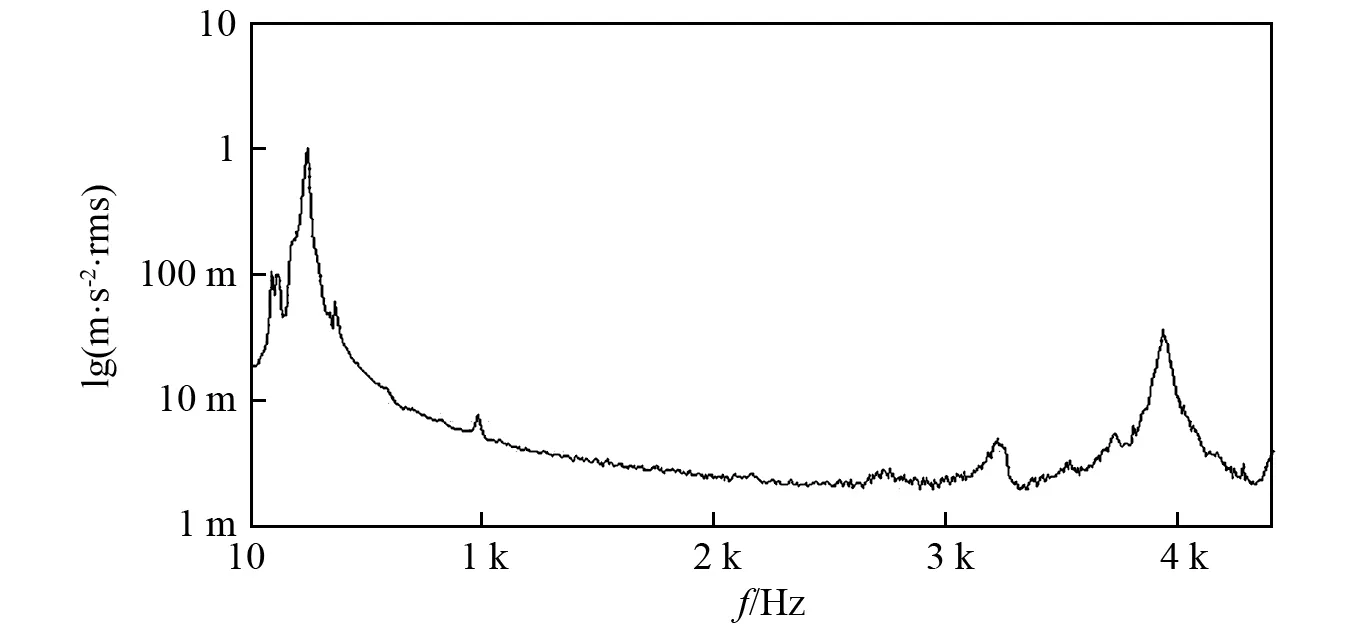
图4 镗杆频率响应曲线Fig.4 Frequency response of boring bar

图5 MATLAB计算流程Fig.5 Calculation scheme of MATLAB

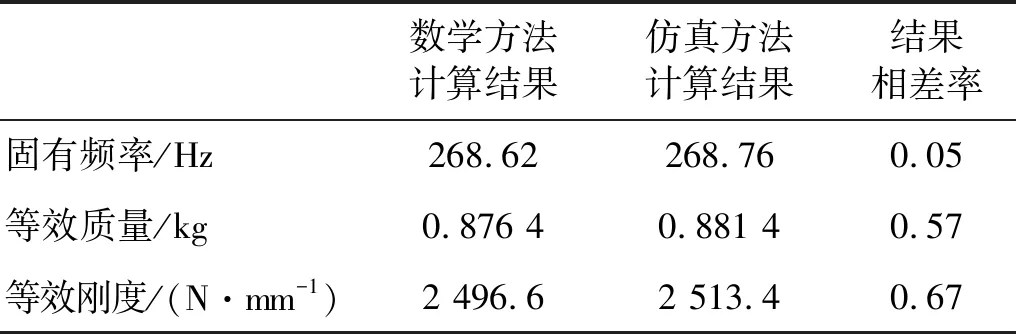
数学方法计算结果仿真方法计算结果结果相差率固有频率/Hz268.62268.760.05等效质量/kg0.876 40.881 40.57等效刚度/(N·mm-1)2 496.62 513.40.67

用ABAQUS软件对减振镗杆主系统进行有限元仿真，首先由模态仿真得到主系统的一阶弯曲模态固有频率为268.76 Hz，结果云图如图6所示。

图6 有限元仿真结果云图Fig.6 Simulation results nephogram

根据质量感应法[12]，在等效位置处增加一定质量，再根据增加质量后固有频率的变化，求解出镗杆主系统的等效质量。Δm为增加的附加质量，Ω为原系统固有频率，ω为增加附加质量后系统固有频率。

(21)

在镗杆等效位置设置一个RF参考点，并指定附加质量为0.2 kg，添加附加质量后镗杆模态发生变化，附加质量后主系统的一阶弯曲模态固有频率为242.64 Hz。质量感应法计算结果如表2所示，由表2可以看出，仿真计算结果与本文提出的数学计算结果相比，固有频率仅相差0.05%，等效质量相差0.57%，等效刚度相差0.67%，说明本文提出的数学计算方法是准确的。

为了对比将减振镗杆作为非等截面梁和等截面梁的计算精度，本文对镗杆截面进行以下两种处理，并与本文提出的非等截面数学计算结果进行比较，验证将镗杆作为非等截面计算的必要性。

第一种等截面方法为将内径按长度加权平均，即截面大小为

外径D不变

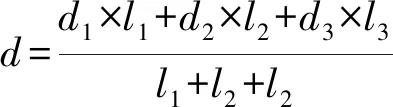
第二种等截面方法为将截面积和惯性矩按长度加权平均，即截面大小为

此动力减振镗杆主系统等效参数按照等截面计算的结果如表3所示。可以看出将减振镗杆作为等截面计算与非等截面计算结果相差较大，说明将减振镗杆作为非等截面计算十分必要。

表3 等截面方法计算对结果的影响

5 结 论

本文针对采用实验和仿真的传统等效参数识别方法效率不高的问题，提出了一种新的识别动力减振镗杆主系统参数的简便高效的数学计算方法，通过仿真验证了所提出方法的有效性。主要结论如下：

(1)新的数学计算方法在建立镗杆固有模态数学模型的基础上，通过数值方法识别出动力减振镗杆主系统的等效参数，为动力减振镗杆吸振器参数优化设计奠定了基础。

(2)根据新的数学计算方法编制计算机软件，只需更改几个简单尺寸参数，即可计算出不同型号、不同设计尺寸的减振镗杆主系统的等效参数，提高了动力减振镗杆的设计效率。

(3)本文所提出的数学方法可直接获得等效参数，而有限元方法还需联合应用质量感应法；而且，当减振镗杆尺寸型号变化后有限元法仍需重复前处理和求解计算及质量感应法的过程，所需时间远远大于本文所提出的数学方法。

(4)将镗杆视为非等截面梁比作为等截面梁计算更为准确，而且此计算方法简单易行，也可适用于其他机械结构不等截面梁的等效参数计算。