Effective Thermal Conductivity for 3D Five-Directional Braided Composites Based on Microstructural Analysis

ZHAO Xiao，MAO Junkui，JiANG Hua

1.Key Laboratory of Aerospace Power System，College of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China；

2.Cummins（China）investment Co.，Ltd.Beijing 100020，P.R.China

3.Commercial Aircraft Corporation of China Ltd.Shanghai，200126，P.R.China

Abstract: A method for predicting effective thermal conductivities（ETCs）of three-dimensional five-directional（3D5D）braided composites is presented. The effective thermal conductivity prediction method contains a digital image processing technology. Multiple scanning electron microscopy（SEM）images of composites are analyzed to obtain actual microstructural features. These actual microstructural features of 3D5D braided composites are introduced into representative volume element （RVE） modeling. Apart from applying actual microstructural features，compression effects between yarns are considered in the modeling of RVE，making the RVE more realistic. Therefore，the ETC prediction method establishes a representative unit cell model that better reflects the true microstructural characteristics of the 3D5D braided composites. The ETCs are predicted with the finite element method. Then thermal conductivity measurements are carried out for a 3D5D braided composite sample.By comparing the predicted ETC with the measured thermal conductivity，the whole process of the ETC prediction method is proved to be effective and accurate，where a relative error of only 2.9 % is obtained.Furthermore，the effects of microstructural features are investigated，indicating that increasing interior braiding angles and fiber fill factor can lead to higher transverse ETCs. Longitudinal ETCs decrease with increasing interior braiding angles，but increase with increasing fiber fill factor. Finally，the influence of variations of microstructure parameters observed in digital image processing are investigated. To explore the influence of variations in microstructural features on variations in predicted ETCs，the actual probability distributions of microstructural features obtained from the 3D5D braided composite sample are introduced into the ETC investigation. The results show that，compared with the interior braiding angle，variations in the fiber fill factor exhibit more significant effects on variations in ETCs.

Key words: effective thermal conductivity;digital image processing;variation;3D five-directional braided composites

0 introduction

The turbine inlet temperature for high performance aeroengines is expected to be greater than 1 900 K［1］，which is far above the melting point of conventional metal alloys. Ceramic matrix composites（CMCs）are considered as alternative materials to metal alloys to address this challenge. in particular，three - dimensional five - directional（3D5D）braided CMCs have attracted considerable attentions owing to their advantages of high temperature capability and lower density compared with metal alloys. in recent years，3D5D braided CMCs have already been employed in practical engineering applications，including high temperature components of aeroengines［2］.

The thermal conductivity of 3D5D braided composites exhibits obvious anisotropy，which significantly increases the complexity and difficulty of predicting temperature fields and life span of high temperature components in aeroengines. Thus，effective thermal conductivities（ETCs）of composites have been one of the research hotspots［3-6］.

Representative volume element（RVE）method［7-8］was commonly applied to investigate effective mechanical properties of 3D5D braided composites.A great deal of research has been done in the field of mechanics［9-11］. A representative unit cell of composites rather than a complete structure was studied in these work. Zhang et al.［12］proposed three types of unit-cell models for predicting the effective stiffness.Li et al.［13］employed the RVE method to investigate the effective elastic properties and the mesoscale mechanical responses.

Few studies have focused on the ETCs of 3D5D braided composites. Li et al.［14］and Lu et al.［15］established the RVE models under the assumption of uniform yarn cross-sections and calculated ETCs of 3D5D and 3D full 5D braided composites，respectively. in fact，cross sections of axial yarns were variable along central axes due to lateral compression from adjacent yarns. if this compression effect was ignored，the fiber fill factor could be greater than 1 in some cases，which was obviously not possible［16］. To simulate effective elastic properties of 3D5D braided composites accurately，Li et al.［16］proposed a RVE model in which cross sections of axial yarns were variable. However，this RVE model has not been validated for investigation of thermodynamic properties.

it could be concluded that more accurate descriptions about microstructural features during RVE modeling could lead to better analysis work of ETCs. To get practical descriptions about microstructural features of composites，digital image processing technologies were introduced. in this way，microstructural features that were actual rather than arbitrarily determined by researches could be incorporated into RVE models. Li et al.［17］applied digital image processing to extract outlines of reinforced particles from scanning electron microscopy（SEM）images of composites and the results of uniaxial tension behavior agreed well with experimental data. Jiang et al.［18］developed a digital image processing method to establish a series of RVEs for unidirectional fiber reinforced composites to predict ETCs.The relative error between the calculated and experimental data was 5.3%.

Microstructural parameters of an actual 3D5D braided composites sample could not be ideally uniform. in fact，they are distributed over a specific range due to the special braiding and reinforcing processes employed during production of materials，which is referred as variations of microstructural parameters. Variations of microstructural parameters result in variations of thermal conductivities. The thermal conductivities of composites of even the same batch are different due to the heterogeneity inside 3D5D braided composites. Then it is difficult to rely on experimental means to get statistical data to investigate the effects of variations of microstructural parameters. Therefore，a method based on probability distributions was introduced into ETC predictions to study these effects. Yan et al.［19］obtained statistical results for ETCs of unidirectional fiber reinforced composites by calculating the statistical characteristics of microstructural parameters. Zhao et al.［20］developed a probabilistic propagation model for assessing the uncertainty in ETCs for ceramic fiber blanket composites. However，these studies were conducted by assuming probability distributions of microstructural parameters rather than actual probability distributions based on real composite samples. it could be expected that introduction of realistic probability distributions during ETC calculations would provide more detailed information about effects of variations in microstructural parameters on variations in ETCs.

in this paper，an ETC prediction method was proposed for 3D5D braided composites. To extend the application of the RVE model［16］to thermodynamic properties investigations，compression effects between yarns were considered in the RVE modeling. With digital image processing technology developed，actual microstructural parameters applied in the RVE modeling were obtained by analyzing multiple SEM images. Then finite element method was applied to predict ETCs. The whole processes of ETC prediction method were then validated by comparing the calculated ETCs with measured thermal conductivities of the 3D5D braided composite sample. The effects of microstructural features（i.e.，the interior braiding angle and the fiber fill factor）were also investigated. Finally，the effects of variations in microstructural parameters on variations in calculated ETCs were studied，during which realistic probability distributions obtained from digital image processing were being introduced into simulations to get statistical results for ETCs.

1 Topological Model

The RVE model of 3D5D braided composites can be built according to the movement of braiding yarns during the fabrication process. Details of the fabrication process can be found in Ref.［8］. The topological structure of the RVE model is illustrated in Fig.1，where the z axis of the global coordinate system is the braiding direction，γ is the interior braiding angle，and h is the height of the RVE. The RVE model contains 14 braiding yarns. The nine points indicate the positions of axial yarns whose directions are parallel with the z axis.

Several basic assumptions have been applied to RVE modeling. The braiding yarn has a constant hexagonal cross section，as shown in Fig. 2（a）.The axial yarn cross-sectional shapes are variable along their axes，and are treated as a square at the z = 0 plane，as shown in Fig.2（b）. The thermal contact resistances between the yarns and the matrix are ignored，as has been done in Ref.［14］.

Fig. 1 Schematic of the representative volume element

Fig.2 Schematics of the cross-sectional shapes of yarns

Eq.（1）can be obtained by the projection relationship.

The RVE width w and thickness t can be determined by Eq.（2）. The parameters b and e are shown in Fig.2.

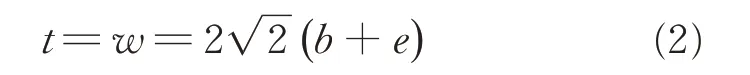
A single yarn consists of N fibers of diameter d，and the total cross-sectional area of N fibers is S.Thus S can be expressed by Eq.（3）. N and d are the known parameters determined during the production of the 3D5D braided composite sample. in this paper，the values of N and d are 1 000 and 12 μm，respectively.

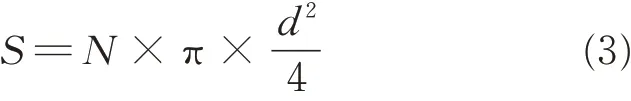
where S1and S2are the cross-sectional areas of the braiding yarns and the axial yarns，respectively.And they can be determined by Eqs.（4），（5）.They also can be expressed by Eqs.（6），（7）. ε1and ε2are the fiber fill factors of the braiding and axial yarns，respectively. The fiber fill factor represents the area ratio of fibers in the yarn cross section.

According to Eqs.（1）—（7），the geometrical parameters of the RVE model shown in Figs.1，2 can be deduced.

According to Eqs.（8）—（12），it can be seen that the RVE model can be established using the parameters γ，S1and S2. According to Eqs.（6）—（7），it can be seen that S1and S2can be determined by ε1and ε2. Since ε1≈ ε2［16］，only one fiber fill factor ε is considered. Therefore，the RVE model can be established once the values of γ and ε are known.

1.1 Determination of interior braiding angle

it is difficult to directly measure the interior braiding angle γ. However，γ can be deduced from the surface braiding angle β. The relationship between them is

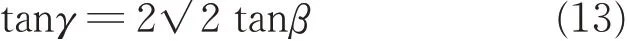
Fig.3 shows the schematic of the braiding yarns on the surface of the 3D5D braided composites. it can be seen that the staggered braiding yarns have only the two directions. and the angle between the two directions is double that of β. The digital image processing technology is developed and employed to measure the angle between the two directions of braiding yarns on the surface of the 3D5D braided composites，then the surface braiding angle β is obtained subsequently.

To effectively apply digital image processing technologies to the 3D5D braided composite surface images to obtain β. it is necessary to obtain surface images of 3D5D braided samples with high resolution，which can be obtained by a Hitachi S3400N instrument. Detailed and informative SEM images can be attained. Prior to SEM images capturing，the sample is subjected to cutting，grinding with metallographic sandpaper，machine polishing，ultra-sonic cleaning，drying，and metal film deposition，which are in accordance with the GB / T 16594—2008 standard specifying general rules for the measurement of micro scale lengths by SEM.A representative surface image of the sample is shown in Fig.4，which clearly shows the two different directions of braiding yarns on the surface of the sample.

Fig. 3 Schematic of braiding yarns on the surface of 3D5D braided composites

Fig. 4 One of surface SEM images of the 3D5D braided sample

Fig.5 Flow chart of line identification

The digital image processing is conducted using Matlab software with self - written program.Fig.5 shows the flow chart of the digital image pro-cessing.First，the regions of braiding yarns are cut out from surface SEM images to filter out unnecessary information and focus on braiding yarns. For example，Fig.6（a）shows a small part of braiding yarns of direction 2. Then median filtering，noise elimination and binarization are applied to enhance the clarity of images. Fig.6（b）shows the binarized image. Then skeleton extraction and Hough transformation - based line recognition are performed.The skeleton extraction is used to refine the features and information in the images，while the Hough transformation is used to detect possible lines in images［21］. The processed final image of Fig.6（a）is shown in Fig.6（c），where the features and information are presented in a more elaborate way. After the Hough transformation is accomplished，the program will output the angles of lines in the images，which represent the directions of braiding yarns. The whole process can be conduct on any area of interest on the surface SEM images.The angle between the two directions of braiding yarns is double of β. The proposed digital image processing technology can be applied to any 3D5D braided composite samples to obtain the actual interior braiding angle of the samples.

Fig.6 Schematic of the digital image processing

To eliminate errors caused by random sampling，multiple SEM images obtained in different areas of the 3D5D braided composite sample surface are analyzed using digital image processing to determine the value of β. Fig.7 shows the results of interior braiding angle γ deduced from β using Eq.（13）.A Gaussian distribution fits the results very well.The average and standard deviation of γ are 43.87°and 2.19°，respectively. The ratio of the standard deviation to the mean value（i.e.，the coefficient of the interior braiding angle）is 0.05. it can be seen that the actual values and the distribution characteristics of the interior braiding angle are demonstrated by digital image processing. The distribution characteristics will be used to study the effects of variations in microstructural parameters.

Fig.7 Results of the interior braiding angles

1.2 Determination of fiber fill factor

in Fig.8，the fibers are not in perfect contact with each other. According to Ref.［4］，the fibers of braiding and axial yarns are typically assumed to be arranged in a regular hexagon configuration shown in Fig.8. Correspondingly，ε can be calculated by

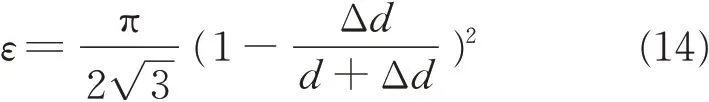
where Δd is the minimum space between fibers.

Fig.8 Schematic of the configuration of individual fibers

Likewise，to eliminate the error caused by random sampling，SEM image capturing is performed in different regions of the sample to measure Δd.The result of ε is 0.8.

1.3 RVE model

Based on the obtained γ and ε，the RVE model shown in Fig.8 can be established. The order of modeling is braiding yarns，axial yarns，matrix. To reflect the compression effects between yarns，the regions of axial yarns that are overlapped with braid-ing yarns are subtracted. in Fig.9，the cross sections of axial yarns are variable along their axes.

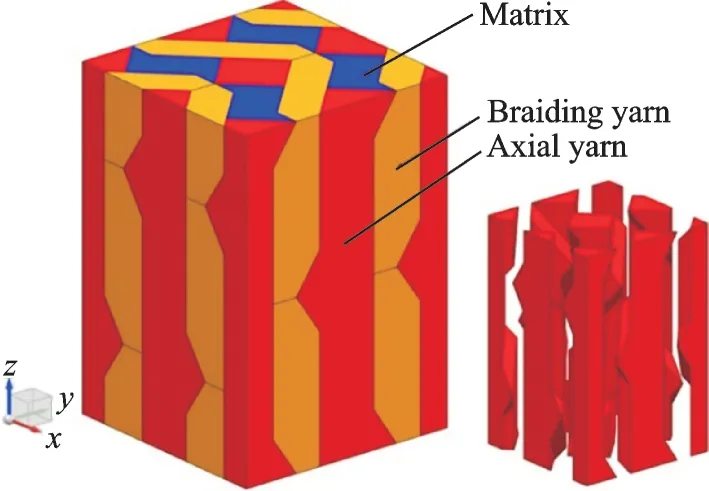
Fig.9 The RVE model

2 Numerical Simulation

2.1 Governing equation

The steady state thermal analysis is programmed under COMSOL Multiphysics software using the default physical model“heat transfer in solids”module. The finite element method is used to solve the following governing equation［5］

where T is the temperature and kij（i，j = x，y，z）are the the non-isotropic thermal conductivities.

2.2 Material properties

The axial thermal conductivities of yarns k∥can be calculated by the mixture law［22］

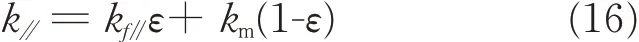
where kf∥is the axial thermal conductivity of fibers and kmthe thermal conductivity of the matrix.

The transverse thermal conductivities of yarns k⊥can be calculated by the Rayleigh equation［22］

where kf⊥is the transverse thermal conductivity of fibers，here，kf∥，kf⊥and kmare 12，3.2 and 0.3 W·m-1·K-1，respectively，which are measured by material producers. To predict ETCs，thermal conductivities of yarns in local coordinate systems must be transformed to be consistent with the global coordinate system，as shown in Fig.1. The knowledge about coordinate transformation can be found in Ref.［23］.

2.3 Boundary conditions

To calculate the ETC along the z direction，isothermal boundary conditions are set on faces z =0 and z = h，while the other faces are set to adiabatic boundary conditions［18］. A similar method can be used to set the boundary conditions to calculate the ETC along the x and y directions. The temperature difference between the isothermal boundaries is expressed by ΔTb= T2- T1，where the lower temperature is denoted as T1and the higher temperature is denoted as T2. in this paper，T1= 293.15 K and T2= 393.15 K.

2.4 Mesh

The RVE is meshed with triangular elements.The mesh of regions where the matrix contacts the yarns is refined to accurately capture high temperature gradients at interfaces. A grid density dependence study was conducted，and the results are listed in Table 1. The medium density grid is adopted in the present study because the difference between the transverse ETCs（i.e. k22）is only 0.08% when increasing the total number of mesh elements from 236 229 to 1 119 064.

Table 1 Grid density dependence results

2.5 Results of ETCs

After numerical simulations are completed，the ETC can be obtained by the Fourier's heat conduction law.The longitudinal ETC is defined as

where qzaveis the average heat flux along the z direction.The transverse ETCs are similarly described as

where qxaveand qyaveare the average heat fluxes along the x and y directions，respectively. The calculated ETC results are summarized in Table 2.

Table 2 ETC prediction results W·m-1·K-1

2.6 ETC prediction method

The method for predicting ETCs of 3D5D braided composites is summarized in this section.Here are the steps involved in the ETC prediction method：

（1）Obtain the interior braiding angle and the fiber fill factor. This is achieved by applying digital image processing technology to analyze SEM images.

（2）Establish the RVE model. in the modeling process，the compression effects between yarns are considered.

（3）Determine material properties as described in Eqs.（16）—（17）.

（4）Mesh the RVE.

（5）Apply boundary conditions to solve the governing Eq.（15）.

（6）The ETCs are finally derived from Eqs.（18）—（20）.

3 Validation

To verify the accuracy of the proposed ETC prediction method，thermal conductivity measurements are performed on the 3D5D braided composite sample studied. The measurement is commissioned to NETZSCH institute of science and technology commerce（Shanghai）Co.，Ltd. applied laboratory. To meet the measurement requirements，the 3D5D braided composite sample shown in Fig.10 is manufactured into a thin cylinder with a diameter of 12.6 mm and a thickness of 4 mm. Thus，the sample is only suitable for measuring one of the transverse ETCs（i.e.，k22）. The 3D5D braided preform is firstly fabricated with silicon carbide yarns.After the preform is immersed in the polycarbosilanes solution and dried，the preform is then burned in a high temperature furnace，during which the polycarbosilane decomposes and bones with the preform.

Fig.10 3D5D braided composite sample

The thermal conductivity of the studied sample is obtained from Eq.（21）

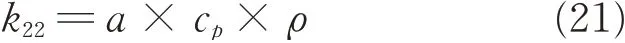
where a is the thermal diffusion coefficient cp，is the specific heat capacity，andis the density of the studied sample.

The thermal diffusion coefficient is measured by a NETZSCH LFA 457 MicroFlash instrument.The measurement method is laser flash method. After the bottom of the sample is irradiated by a bunch of instantaneous light pulses，the temperature of the upper surface of the sample will increase accordingly. The curve of the center temperature of the upper surface with time will be completely recorded. Then a can be calculated by

where tsampleis the thickness of the studied sample，and τ1/2represents the time that it takes the sample surface temperature to rise to half the maximum.

The thermal diffusion coefficient is measured by a DSC 200 F3 instrument. The measurement method is differential scanning calorimetry. The sample is heated at 5 K/min during the measurement to obtain the curve of the heat flow rate with the heating rate，so that the specific heat capacity of the sample is obtained according to Eq.（23）

where q is the heat flux and m is the mass of the studied sample.

Comparing Tables 2，3，it can be found that the difference between the predicted and the average experimental value of k22is 2.9%. The good agreement provides strong support to the reliability of the proposed ETC prediction method. The error may be the results of unknown gaps and holes inside the sample.

Table 3 Thermal conductivity measurement results

4 Effects of Microstructural Features

As discussed above，the interior braiding angle γ and fiber fill factor ε are critical parameters that determine the RVE. Therefore，this section will investigate the effects of γ and ε on ETCs. γ varies from 20° to 60° and ε is set as 0.3，0.5，0.7，0.8，and 0.9. To adapt the method to the general cases，the thermal conductivities of fibers and matrix employed in this section and in the next section are derived from Ref.［14］，where kf∥，kf⊥and kmare 8，1 and 0.18 W·m-1·K-1，respectively. The predicted longitudinal ETC k11and transverse ETC k22are presented in Figs.11，12 as functions of γ and ε，respectively. The following analysis focuses on k11and k22because the calculated values of k22and k33are almost equal.

Fig.11 shows that，when ε is constant，k11decreases and k22increases as γ increases. This trend is consistent with the trend mentioned by Li et al.［14］.The transverse thermal conductivity of braiding yarns is less than that along the longitudinal direction. As γ gradually increases，the transverse direction of braiding yarns gradually coincides with the longitudinal direction of RVE，which contributes to the decline of k11. Meanwhile，with the increase of interior braiding angle，the longitudinal direction of braiding yarns gradually becomes identical with the transverse direction of RVE，which causes the increase of k22.

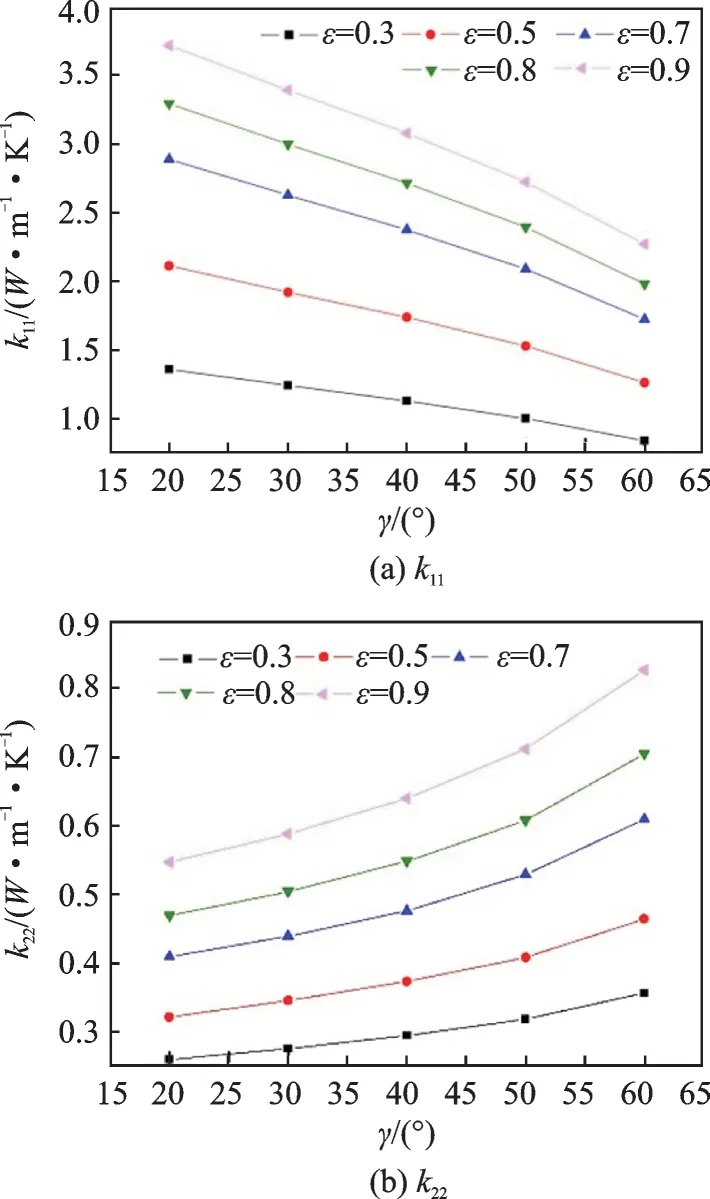
Fig.11 ETCs variation with the internal braiding angle γ

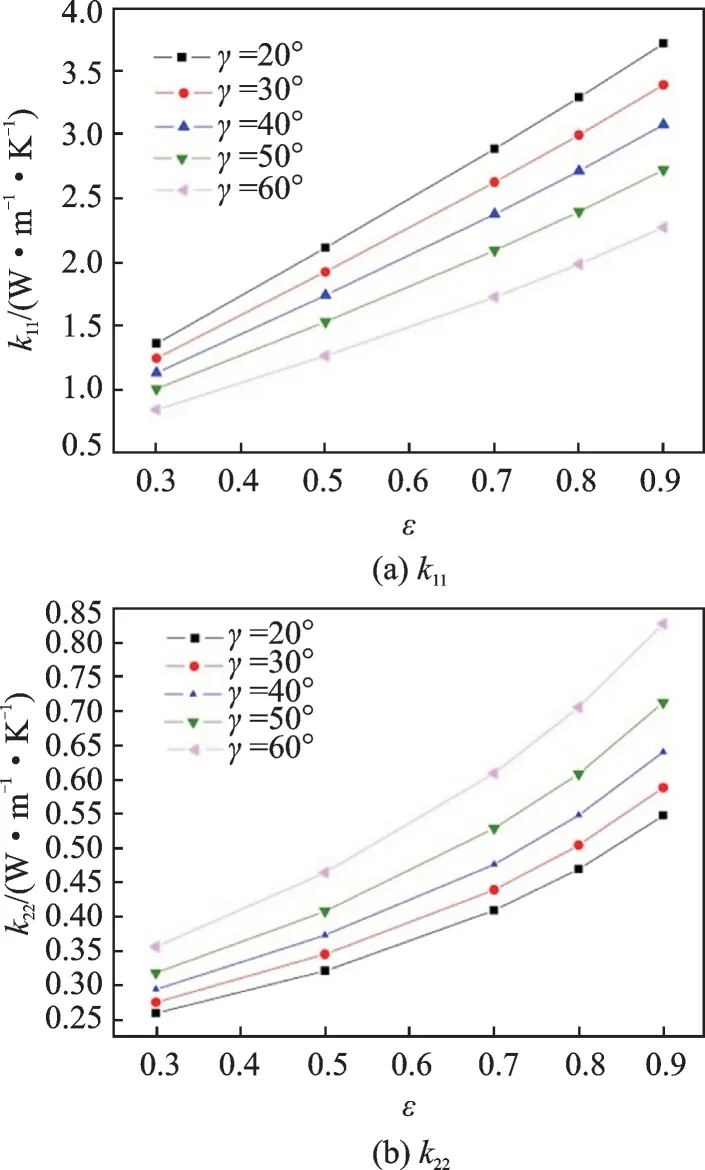
Fig.12 ETCs variation with the fiber fill factor ε

in Fig.12，both k11and k22increase with the in-crease of ε. When γ = 40°，k11and k22more than double as ε increases from 0.3 to 0.9. The proportion of the fiber phase inside the RVE model increases with increasing ε. and thermal conductivity of fibers is greater than that of the matrix. Thus，both k11and k22increase with increasing ε.

5 Effects of Variations in Microstructural Features

The interior braiding angle γ is sampled according to a normal distribution，as shown in Fig.7. For fiber fill factor ε，it is assumed that ε varies in a normal distribution as well. The mean values of γ and ε are derived from digital image processing，which are 43.87° and 0.8，respectively. The coefficient of variation（CV）is the ratio of the standard deviation to the mean value and is used here to assess the level of variation. The CVs of γ and ε are set to 0.5，0.2，0.1，0.05，and 0.01 in this paper. Normal distributions can therefore be determined using the mean values and the CVs. To get statistical results of variations in ETCs（i.e.，the CVs of ETCs），the ETCs simulations are performed with 200 groups of γ and ε randomly sampled from normal distributions.

The relationship between CVETC（i.e.，the coefficient of variations in ETCs）and CVγ（i.e.，the coefficient of variation in γ）is shown in Fig.13. The figure indicates that the variations in the ETCs correlates positively with the variations in γ，that is，when the variation of γ decreases，the ETCs are distributed closer around the mean value.

The relationship between CVETCand CVε（i.e.，the coefficient of variation in ε）is shown in Fig.14. The figure indicates that the variations in the ETCs are also positively correlated with the variation in ε. Thus，the ETCs are distributed closer around the mean value as the variation of ε decreases.

The dashed blue lines in Figs.13，14 are reference lines whose slopes are one. Compared with Fig.13，the curves in Fig.14 are closer to the reference line，indicating that the variation in ε has a greater influence on variations in ETCs.

Fig.13 CVETC variation with CVγ

Fig.14 CVETC variation with CVε

6 Conclusions

An innovative method of predicting ETCs of 3D5D braided composites is established. The thermal conductivity of a 3D5D braided composite sample was measured to validate the proposed ETC prediction method. The effects of microstructural features on ETCs are studied. The effects of variations in microstructural features on variations in ETCs are also investigated. The following conclusions are derived：

（1）The proposed method effectively predicts the ETCs for 3D5D braided composites. The digital image processing technologies provide actual values and distribution characteristics of 3D5D braided composite microstructures. The RVE model，which employs the actual values of microstructural features and considers the compression effects of yarns，shows good performance in ETC predictions. The relative error between the predicted value and the experimental data is only 2.9%.

（2）The longitudinal ETC decreases with an increasing interior braiding angle，but increases with an increasing fiber fill factor. An increased interior braiding angle or a fiber fill factor results in higher transverse ETC.

（3）The variations of ETCs are positively correlated with the variations of γ and ε. Variations in the fiber fill factor exhibit a more significant effect on variations in ETCs.