Self-Sensing Test Method for the Temperature of Piezoelectric Stacks

SHEN Xing，Li Yang，LiANG Lei*，DAi Yuke，CHEN Yuchen，YANG Jinchuan

1.State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China；

2.Low Speed Aerodynamics institute，China Aerodynamics Research and Development Center，Sichuan 621000，P.R.China

Abstract: A self-sensing test method for the temperature of piezoelectric stack，based on the high correlation between the static capacitance and the stack temperature，is proposed in order to construct a self-sufficient methodology of temperature measurement. Firstly，a theoretical model of static capacitance of the piezoelectric stack under preload was set up，and the influence of preload on the static capacitance was analyzed. Secondly，the correctness of the model was verified by static capacitance test experiments under various preloading conditions. Finally，the temperature measurement experiments at low-temperature stage for two kinds of piezoelectric stacks，namely the lowtemperature - resistant piezoelectric stack and conventional piezoelectric stack，were conducted under various preloading conditions using a polynomial fitting method. The results，which validate the accuracy of the test method，show that the maximum temperature deviations of the two kinds of piezoelectric stack are 3.9 ℃ and 2.8 ℃ ，respectively，when the preload force is close to the specified value. The test method uses the piezoelectric stack itself as a temperature sensor，which does not require additional equipment for temperature sensing，so that the space and equipment cost could be economized. and the test for static capacitance is concise and convenient，which indicates that in the cooling process，a concise and efficient test of the temperature of the piezoelectric stack could be realized so as to grasp the current temperature change in time.

Key words: temperature test;piezoelectric stack;static capacitance;preload;curve fitting

0 introduction

Piezoelectric materials，characterized by high electromechanical conversion efficiency， fast response and low power consumption，have been widely used in precision structure actuation，vibration control and noise control，etc.［1-2］. Piezoelectric stack that features high force has been increasingly applied to environments with temperature variation，radiation，vacuum，especially in application occasions where the ambient temperature must fall to a low value in recent years［3-4］. More example could be given such as active vibration control of the cantilever sting realized by using piezoelectric stack in the cryogenic wind tunnel［5-7］，where the ambient temperature will decline blew -150 ℃due to liquid nitrogen spray；the piezoelectric stack is used as a force sensor and vibration controller in cryogenic super-conducting cavities［8］，the temperature in which shall drop to -268.98 ℃；and it is used as a micro displacement positioning actuator in cryogenic optical system，where the piezoelectric stack was subjected to temperature ranging from 50 ℃to-130 ℃.Both properties and driving characteristics of the piezoelectric stack are vulnerable to the influence of temperature drop［9-10］. it is even likely to cause damage or failure of the epoxy resin inside if the piezo-electric stack's temperature exceeds the preset temperature or its own ultimate temperature during the temperature drop. The majority of current researches tends to focus on the effect of temperature variation on the properties of piezoelectric materials such as static capacitance［11-13］and impedance［14-15］. However，temperature tests based on the fact that properties of piezoelectric materials would vary with temperature were rarely carried out in existing literatures. For instance，Nouroz et al.［16］studied the relationship between the impedance of piezoelectric patches and the temperature as well as its own strain，and then concluded that the temperature and strain could simultaneously be determined by impedance test，from 20 ℃to 60 ℃. The maximum deviation of measured temperature was ±3.5 ℃. Jürgen et al.［17］took independent piezoelectric patches in various types and piezoceramic composites as test objects，its temperature could be similarly determined also by impedance test and the maximum deviation was ±4.5 ℃from 0 ℃to 100 ℃. Therefore，test objects of all relevant research have been piezoelectric patches and only the temperature measurement at a high-temperature stage has been realized basically by means of the impedance，which indicates a lack of test statistics and research results on piezoelectric stack at low temperature.

in this paper，a self-sensing test method for the temperature of piezoelectric stack，based on the high correlation between the static capacitance and the stack temperature，is proposed. The corresponding temperature can be calculated by a fitting function after the static capacitance is measured at lowtemperature stage. The presented method can be utilized for additionally sensing temperature in devices with integrated piezoelectric stack，and it can save costs and deal with the difficulty in adding additional temperature sensors to the narrow assembly space for piezoelectric stack［18］. A rough knowledge of the temperature in the observed object is important information to the user. For example，the exceedance of a certain low temperature limit could be detected easily and avoided timely with the aid of the static capacitance of the piezoelectric stack.

1 Theoretical Model for Static Capacitance Under Preload

When an external force acts on the piezoelectric patch，the two electrode plates of the piezoelectric patch will be conferred with electric charges opposite in polarity and equal in electric quantity. Therefore，the piezoelectric patch can be regarded as a plate capacitor with opposite charges accumulated on the two electrode plates and an insulator in the middle. Piezoelectric stack consists of multiple layers of piezoelectric patches with the same electromechanical characteristics combined mechanically in series and electrically in parallel.

According to the equation for calculating parallel-plate capacitance，the capacitance of piezoelectric stack in a free state is expressed as

where A is the cross-sectional area of the piezoelectric stack，t is the thickness of the piezoelectric patch，n is the number of piezoelectric patches，andis the dielectric constant in the polarization direction（z-axis）.

Due to the weak resistance to tension of the piezoelectric stack，it is necessary to apply certain compressive preload force Fpreon it by means of external mechanical structure in practice to prevent the stack being exposed to tensile stress. Then，the stack will be subjected to pre-compressive deformation and its output displacement will be reduced when driven. Consequently，a model for the piezoelectric stack under preload is constructed according to the actual situations：the preload force applied to the piezoelectric stack causes a certain degree of deformation ΔL. it is assumed that the stiffness of the external mechanical structure is large enough，namely，the piezoelectric stack is completely subjected to the rigid constraint in the polarization direction，which parallel to its length，as shown in Fig. 1. in ideal conditions，the deformation in the polarization direction will remain unchanged even when the piezoelectric stack is driven，and the strain will keep constant as ΔL/L=Fpre/kL，where k and L are the stiffness and original length of the piezoelectric stack，respectively.

Fig.1 Diagram of piezoelectric stack under preload

Piezoelectric constitutive equations in the polarization direction are as follows［19］

where S3is the strain，T3is the stress，D3and E3are the electric displacement and electric field in the polarization direction，respectively.

Piezoelectric equations of piezoelectric stack under preload are as follows

it is assumed that the total quantity of electric charge of the piezoelectric stack is Q when the testing voltage U is applied to two electrodes of the piezoelectric stack. Then，the overall capacitance of the piezoelectric stack under preload will be as follows according to the equation of capacitance definition

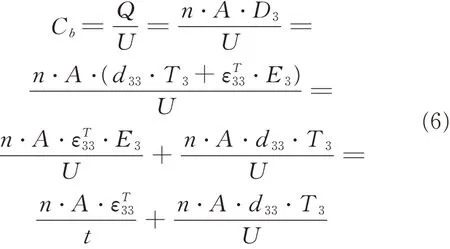
By substituting Eqs.（1），（5）into Eq.（6），the following equation can be obtained.

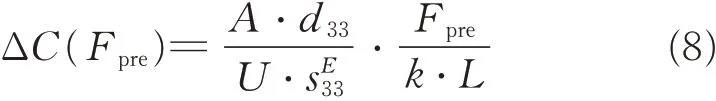
Within a certain range of temperature drop，a fitting function based on the relationship between the capacitance of piezoelectric stack and the temperature variation under preload can be obtained through the polynomial curve fitting. Then，during the temperature decline，the corresponding temperature can be determined after the capacitance of the piezoelectric stack is tested and substituted into fitting function. According to Eq.（8），the capacitance of the stack will increase under preload force，so the relationship between capacitance and temperature may be different under various preloading conditions，and the increase is correlated with parameters of the piezoelectric stack as well as the preload force applied. As a result，the correctness of the theoretical model needs to be validated through experi-ments.

2 Experiments and Analyses

2.1 Experimental apparatus

Two kinds of piezoelectric stacks are employed in the test.One was low-temperature-resistant piezoelectric stack（PSt 150/20），which was subjected to temperature drop from 20 ℃to -50 ℃in the experiment，the other was conventional piezoelectric stack（PSt 150/VS15），which experienced temperature drop from 20 ℃ to - 20 ℃ ，as shown in Fig.2.

Fig.2 Two kinds of piezoelectric stacks

The experimental setup for applying mechanical loads to piezoelectric stack was designed and manufactured，as shown in Fig. 3. The piezoelectric stack was installed on the pressure sensor and clamped between the upper and the lower disks that were connected through four bolts. Different preload forces，measured by a pressure sensor，could be applied to the piezoelectric stack by adjusting the preload nuts on the bolts. in all cases，the compressive stress was parallel to the polarization direction.Thermistor temperature sensor was connected to the stack，whose actual temperature was measured.

The experimental setup was placed in a lowtemperature test chamber. The displays of both the pressure sensor and temperature sensor were placed outside the test chamber. The data cable connected the internal sensor with the external display instrument through the hole at the side of the test chamber. Similarly，the coaxial cable of the piezoelectric stack was also left outside the chamber and linked with LCR testing instrument，which is feasible to test inductance，capacitance and resistance，so as to measure the capacitance of the stack directly，as shown in Fig.4. Among them，the testing voltage of LCR instrument was 150 mV，and the testing frequency was 100 Hz，which was far below 50 kHz，the resonant frequency of piezoelectric stack. Therefore，the measured capacitance is static. in the experiment，a low-temperature pressure sensor（LKL-102L-type）；a thermal resistance temperature sensor（WZP）；an LCR testing instrument（ViCTOR 6243-type），and a low-temperature test chamber（HRH0270-type）were adopted.

Fig.3 Experimental setup for applying mechanical loads to piezoelectric stacks

Fig.4 Photograph of the experimental device

2.2 Experiments on the effect of preload force on static capacitance

2.2.1 Experimental scheme

Experiments of the static capacitance variation with the temperature for the two kinds of piezoelectric stacks in the free state have been conducted.The cooling rate of the low-temperature chamber was 2 ℃/min，and the capacitance was measured at every 3 ℃interval during the temperature decline.Then，the static capacitance-temperature relationship curves were obtained，and two fitting functions for the piezoelectric stacks were derived via curve fitting based on the quadratic polynomial model，as shown in Fig. 5. The correlation coefficient of the fitting result R2，has turned out to be larger than 0.99 in both experiments，indicating that there is a high correlation between the static capacitance and temperature.

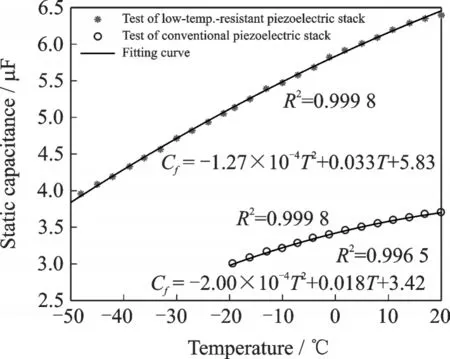
Fig.5 Curve-fitting results of static capacitance of two kinds of piezoelectric stacks varying with temperature in free state

After that，at room temperature of 20 ℃ ，preload forces of 870 N and 320 N were applied to the low -temperature -resistant piezoelectric stack and conventional piezoelectric stack，respectively. Then similar experiments were also conducted. Thus，the experimental results illustrating the temperature variation with the static capacitance of the two piezoelectric stacks under preload were obtained.

2.2.2 Verification experiments results on the low - temperature - resistant piezoelectric stack

Relevant parameters of two kinds of piezoelectric stacks provided by the manufacturer are shown in Table 1. Besides，Refs.［21-22］shows that the measurement of the electromechanical coupling factor of piezoelectric ceramics K33，basically remains constant within the range from room temperature to-50 ℃. To facilitate the calculation，it is assumed that the values of K33of both piezoelectric stacks are constant.

Table 1 Parameters of two kinds of piezoelectric stacks

The increase in capacitance，which could be calculated by the equation ΔC（Fpre）=3.32 μF，was obtained by substituting parameters of low-temperature-resistant piezoelectric stack in Table 1 into Eq.（8）. By substituting them into Eq.（7）with the capacitance - temperature fitting function in the free state，the theoretical capacitance-temperature relationship under preload can be obtained.

The theoretical results are plotted and then contrasted with the experimental results，as shown in Fig.6.

The results show that，with a preload force of 870 N，the static capacitance increases to some extent and the static capacitance -temperature curve moves upward as a whole，which is consistent with the theoretical analysis in Section 1. Moreover，at the temperature of 20 ℃，the experimental value of capacitance is 6.69 μF with the theoretical value being 6.79 μF，which means there is a deviation of 1.5% between the two values. However，as the temperature decreases，the deviation between experimental and theoretical values increases gradually.

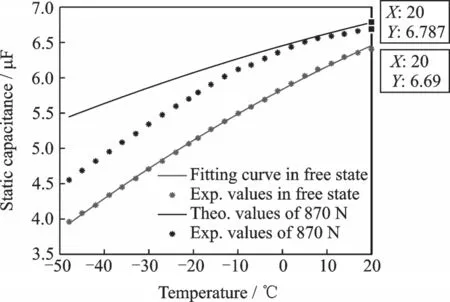
Fig.6 Comparison of theoretical and experimental values of capacitance -temperature relationship of the low-temperature-resistant piezoelectric stack under preload

2.2.3 Verification experiments results on the conventional piezoelectric stack

The increase in capacitance Δ C（Fpre）=2.08 μF，which can be calculated by the substitution of parameters of conventional piezoelectric stack in Table 1 into Eq.（8）. The way to obtain the theoretical capacitance-temperature relationship under preload is the same as that of low -temperature-resistant piezoelectric stack experiment，and the result is

The theoretical results are plotted and contrasted with the experimental results，as shown in Fig.7.

Fig.7 Comparison of theoretical and experimental values of capacitance-temperature relationship of the conventional piezoelectric stack under preload

The results show that，with a preload force of 320 N，the static capacitance-temperature curve also deflects upwards as a whole，which is in accordance with the theoretical analysis in Section 1. Besides，at the temperature of 20 ℃，the experimental value of capacitance is 3.84 μF and the theoretical value is 4.07 μF，so the deviation is 5.7%.

Through experiments，the hypothesis that preload force can increase static capacitance of the piezoelectric stack has been verified，and the deviation turns out to be relatively small compared with theoretical results，which has demonstrated the correctness of the theoretical model in Section 1. From Figs. 6，7，however，both comparison results of two piezoelectric stacks have shown that the deviation would increase gradually with the temperature drop，and theoretical values are larger than experimental values in general. The reason lies in that the electromechanical coupling factor K33has been set as constant in the theoretical calculation，while K33would increase with the temperature drop and the augment of preload force in practical experiments.Eq.（7）can be transformed as shown below to facilitate the analysis and explain.

in addition，the deviation of the conventional piezoelectric stack at 20 ℃is relatively larger than that of low-temperature-resistant piezoelectric stack.it is bacause the conventional piezoelectric stack in Fig. 2 is a kind of encapsulation structure，which means its internal pretension springs would provide an extra preload force in addition to the external preload force.

2.3 Temperature measurement experiments based on static capacitance

2.3.1 Experimental scheme

in addition to the temperature，the static capacitance of the piezoelectric stack can also be changed with the preload force according to the analysis above. Consequently it is necessary to test the relationship between the capacitance and temperature of the two piezoelectric stacks under various preloads to investigate the temperature measurement effects of the test method under different preloading conditions.

According to the manufacturers，it is specified that the preload force should be set to around onetenth of the blocking force to ensure maximal lifetime. Since the blocking force of the low-temperature-resistant piezoelectric stack is 7 000 N. Therefore，four preload forces，i.e.，650 N，700 N（the specified value），750 N，and 870 N，have been applied respectively at room temperature of 20 ℃. The blocking force of the conventional piezoelectric stack is 2 300 N，and three preload forces，230 N（the specified value），280 N，330 N，have been applied at the same room temperature，respectively. Firstly，the corresponding static capacitance under different preloading conditions was measured as the initial value C0. Similarly，during the temperature decline at the rate of 2 ℃/min，the capacitance Cbwas measured at every 3 ℃ interval，and the capacitance variation was calculated through equation Δ Cb=Cb-C0. Thus，the capacitance variation-temperature relationship curves of the two piezoelectric stacks under different preloading conditions were obtained.

2.3.2 Temperature measurement results of the low - temperature - resistant piezoelectric stack and discussion

The capacitance variation-temperature relationship curves of the low-temperature-resistant piezoelectric stack are shown in Fig. 8. The results indicate that the curves will move up resulting from the decrease of the capacitance variation when the preload force increases. Moreover，there is a small nonlinear area at the initial stage of temperature decline，after which the curves keep a quasi-linear relation.

The capacitance variation - temperature curve under specified preload force of 700 N was then fitted to obtain a quadratic polynomial fitting function

The capacitance variation under the other three preload forces was tested and substituted into the fitting function to calculate the estimated temperature.Then it was compared with the actual measured temperature to obtain the deviation at every temperature points，as shown in Fig.9.

Fig.8 Capacitance variation-temperature relationship of the low-temperature-resistant piezoelectric stack under different preloading conditions

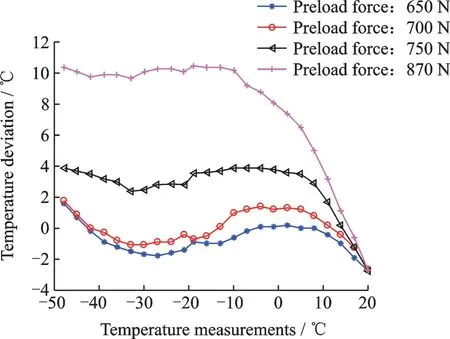
Fig.9 Temperature deviation of low-temperature-resistant piezoelectric stack under different preloading conditions

The maximum deviation and the average deviation were calculated within the temperature measurement range，as shown in Table 2. The results show that the maximum deviation is 3.9 ℃and the average deviation is lower than 3 ℃in a range from 650 N to 750 N of the preload force. Furthermore，the maximum deviation value is 10.5 ℃and the average deviation value is 8.1 ℃ when the preload force is 870 N.Therefore，it indicates that the deviation of temperature measurement is relatively insignificant in the range of 650 N to 750 N，namely，being close to the specified preload force of 700 N.The deviation is relatively large under the condition of excessive preload force. The reason lies in that the curves of capacitance variation over temperature will move up when the preload force increases.Hence，excessive preload force can increase the gap between curves，thereby causing greater deviation.

Table 2 Experimental results of low-temperature-resistant piezoelectric stack under different preloading conditions

2.3.3 Temperature measurement results of the conventional piezoelectric stack and discussion

The capacitance variation-temperature relationship curves of the conventional piezoelectric stack are shown in Fig. 10. The results also indicate that the curves will move up when the preload force increases.

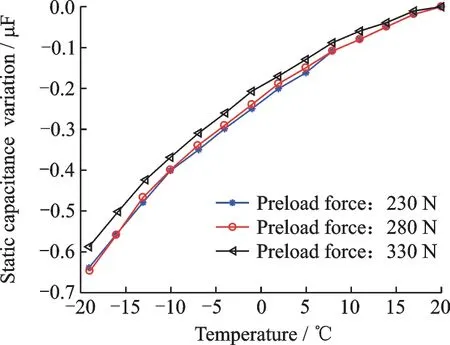
Fig.10 Capacitance variation-temperature relationship of the conventional piezoelectric stack under different preloading conditions

The capacitance variation - temperature curve under specified preload force of 230 N was fitted to obtain a quadratic polynomial fitting function

The capacitance variation under the other two preload forces were tested and substituted into the fitting function respectively to calculate the estimated temperature，the deviation was obtained in the same way as described above for low-temperatureresistant piezoelectric stack，as shown in Fig.11.

Fig.11 Temperature deviation value of conventional piezoelectric stack under different preloading conditions

The maximum deviation and the average deviation were calculated within the temperature measurement range，as shown in Table 3. The results show that the maximum deviation is 2.9 ℃and the average deviation is lower than 2 ℃in a range of 230 N to 330 N of the preload force，which indicates that the deviation of temperature measurement is relatively insignificant in the range of 230 N to 330 N，namely，when it is close to the specified preload force of 230 N.

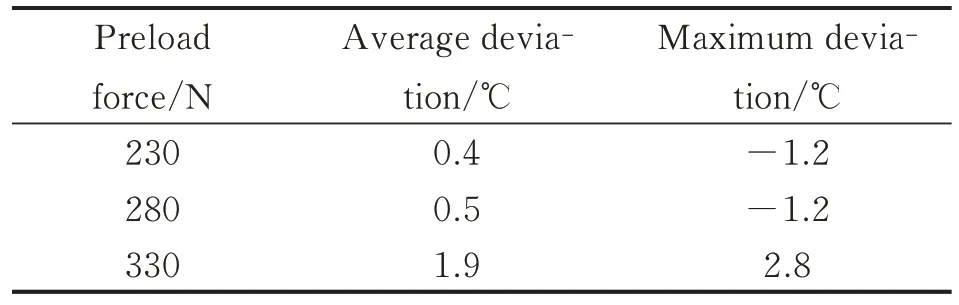
Table 3 Experimental results of conventional piezoelectric stack under different preloading conditions

3 Conclusions

A self-sensing temperature test method was proposed based on the measurement of temperaturedependent capacitance changes of piezoelectric stack. in addition，a theoretical model for static capacitance under preload has been established，which facilitates the analysis of the influence of preload force on static capacitance and the validation of the model's correctness through experiments. Moreover，temperature measurement experiments on the two piezoelectric stacks under various preloading conditions were conducted to prove the feasibility of the test method. The experimental results show that the maximum deviation is 3.9 ℃and the average deviation is lower than 3 ℃in a preload force range of 650 N to 750 N for low-temperature-resistant piezoelectric stack；and for the conventional piezoelectric stack，the maximum deviation is 2.8 ℃and the average deviation is lower than 2 ℃over a preload force range of 230 N to 330 N，which indicates that the deviation of temperature measurement is smaller when it is close to the specified preload force.

The attraction of such a method is that no additional temperature sensor is needed，because the piezoelectric stack can be used as temperature sensors. it is simple and convenient to enhance the experimenter's awareness of the current temperature of piezoelectric stack，which is significant and valuable in taking timely temperature control measures to protect the piezoelectric stack.