High-Order Discontinuous Galerkin Method for Hovering Rotor Simulations Based on a Rotating Reference Frame
2019-04-03ZHANGTaoHongqiangQiNWanglongCHENZhengwu
ZHANG Tao,LÜ Hongqiang*,QiN Wanglong,CHEN Zhengwu
1.Department of Aerodynamics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China;
2.China Aerodynamics Research and Development Center,Mianyang 621000,P.R.China
Abstract: An implicit higher-order discontinuous Galerkin(DG)spatial discretization for the compressible Euler equations in a rotating frame of reference is presented and applied to a rotor in hover using hexahedral grids. instead of auxiliary methods like grid adaptation,higher-order simulations(fourth- and fifth- order accuracy)are adopted.Rigorous numerical experiments are carefully designed,conducted and analyzed. The results show generally excellent consistence with references and vigorously demonstrate the higher-order DG method's better performance in loading distribution computations and tip vortex capturing,with much fewer degrees of freedom (DoF). Detailed investigations on the outer boundary conditions for hovering rotors are presented as well. A simple but effective speed smooth procedure is developed specially for the DG method. Further results reveal that the rarely used pressure restriction for outlet speed has a considerable advantage over the extensively adopted vertical speed restriction.
Key words: high-order method (HOM); discontinuous Glaerkin method (DGM); Euler equation; hovering rotor simulation;tip vortex
0 introduction
Due to the rapid development of high performance computers and numerical algorithms over the last two decades,directly solving the governing equations without attaching any prescribed wake models is becoming the most popular method in rotorcraft computational fluid dynamics(CFD)[1-5].This so-called“first principle method”is theoretically capable of simulating general complicated rotorcraft flow-fields,while the wakes would be synchronously captured as parts of the solution. However,in most cases,the wakes obtained through this methodology disappear so fast due to the numerical dissipation.
Several types of numerical methods[5]have been developed to tackle the problem. Overlapped grids combing with intensive Cartesian or hybrid meshes and adaptation methods are satisfactorily efficient in preserving vortices[6-12](usually implemented with the traditional finite volume(FV)or finite difference(FD)method). Such methods are also able to model the complex blade motions which are common in helicopter flights. Using the vorticity confinement method[13]or applying the vorticity transport equation[14]as the governing equation are also very effective.
Another approach would be the high - order scheme,which is well-known for its outstanding ability in simulating complicated flow structures.Hariharan and Sankar's[15-17]investigations using essentially non-osci-uatory(ENO)scheme proved that high-order schemes are quite effective in capturing vortices. Zhao et al.[18]applied a third-order Roe's flux difference splitting (FDS) scheme in 2005.The results presented showed that those high-order schemes could effectively reduce the numerical dissipation and improve the resolution.
However,another promising high-order method,the discontinuous Galerkin finite element method(DGM),is relatively rare to be seen employed in rotorcraft CFD. Compared with ENO/(WENO)finite difference or finite volume method,the DG method is compact and has fascinating stability properties[19]. For the DG method,the discretization of an element only depends on its neighboring elements. Furthermore,the order of accuracy of each element can be independently changed simply by adopting the basis functions of different orders[20].The DG method is capable of handling complicated geometric and physical boundaries as well[21-22].Thus,the DG method should presumably show a fine performance in rotorcraft CFD.
in 2002,Boelens et al.[23]developed a boundary conforming DG method for the rotorcraft flowfield simulation. The results showed that the DG method captured vortices over large distances,and yielded the same or finer agreement between the numerical and experimental data,compared with other conventional methods. Modisette et al.[24]reached a similar conclusion in 2008.
The above former similar work using DGM both focused on the combination of high-order methods with reasonable accuracy(the third-order accuracy)and grid adaptation methods for better wake capturing. in contrast,we believe that with the same or even fewer amount of variables,higher-order simulation could yield better results than locally increasing the grid density. Therefore,in our work the auxiliary grid adaptation methods are abandoned,instead higher-order(fourth- and fifth- order accuracy)simulations are adopted. Rigorous numerical experiments are carefully designed and conducted. The results obtained here show good consistence with the references using few degrees of freedom(DoFs). After detailed comparison with results from lower-order DGM(the third accuracy)[25]and traditional finite volume method (FVM)[10]both with grid adaption,our work vigorously proves that higher-order methods are much more effective in capturing the wake of rotors than locally increasing the grid density.
in addition,investigations on the influence of outer boundaries for hovering rotor simulations are presented as well. The so-called Jet-Sink boundary conditions[26]for hovering rotors based on theoretical analysis are employed. Further,a simple but effective smooth procedure for the vertical speed near the outlet of the Jet-Sink B.C. is developed for the high-order DGM. Comparied with the original edition,the smooth procedure can eliminate the discontinuity of vertical speed and suppress the non-physical oscillation near the outlet. The solution nearby is hence better resolved and better global convergence can be noticed. Besides,in contrast to most researchers who restrict both speed and pressure in the Jet-Sink B.C.,we adopt a single pressure restriction[1]which is very rare to zero to be seen used.Combining with the aforementioned simple smooth procedure,the pressure restriction condition yields better outlet speed distribution,global solution,and convergence history,which indicate that the rarely used pressure restriction condition has a considerable advantage over the extensively used vertical speed restriction.
Meanwhile,to compare with former results and to reduce the calculation size,the Euler equations are adopted for our higher-order simulations.Though viscosity is ignored in the simulation,the results are still of considerable practical value for engineering applications and vorticity is theoretically allowed. Simulations of the well-known Caradonna-Tung[27]rotor in hover are chosen to validate the numerical methods.
1 Formulation of the DG method
The governing equations in a non-inertial rotating reference frame have been derived through several approaches and already in use by many researchers[1-2,6,24]. in this Section,the compressible Euler equations in such a frame are formulated and examined,and a high-order DG spatial discretization is presented.
1.1 Euler equations in a rotating reference frame

Fig.1 Static Cartesian reference O-xyz and rotating Cartesian reference Or-xyz
As shown in Fig.1,let O-xyz and Or-xyz denote the two Cartesian reference frames which coincide with each other,while Or-xyz has a constant anticlockwise angular velocity ω=(0,0,Ω ). Transformational values in such frames would have relations written below

where V and Vrrepresent velocity vectors in O-xyz and Or-xyz respectively,a and arcorrespondingly denote acceleration vectors in O-xyz and Or-xyz.VΩdenotes the rotational velocity component,while aeand acdenote the convected acceleration and the Coriolis acceleration due to the rotation,respectively(these two accelerations together constitute the inertial acceleration). Further,they are associated with other variants through the equations below

When formulating the governing equations in a non - inertial system,the so - called inertial force could be treated as a body force. Hence,taking such body force and its work into consideration,the three dimensional Euler equations governing the unsteady compressible inviscid flow in a rotating frame of reference can be expressed as

where the conservational variants and flux terms are


The source term Wr,which is the synthesized result of the convected acceleration and the Coriolis acceleration ,can be written as

Considering the work produced by the inertial force,modified definitions of the total energy E and the total enthalpy H might bring us more convenience[27]
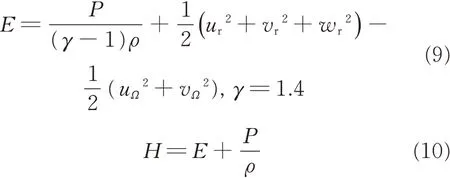
Usually,Eq.(6)is recast in terms of absolutevelocity V using Eq.(1). Since former research[28]suggested that the gap between the speed of the wall surfaces and the speed at far-field in a rotating coordinate is widened,hence more numerical errors would come up and thereby compromising the final accuracy. But before the recast,the relationships between the total energy e,total enthalpy h in the fixed coordinate O-xyz and their counterparts E,H in the rotating frame Or-xyz should be noticed
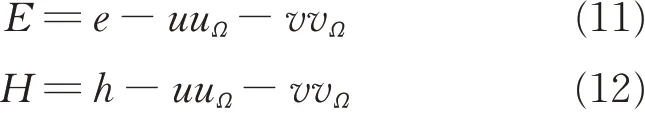
Eq(.6)then becomes

where

Eq.(13)can also be written as

1.2 DG discretization
By introducing suitable piecewise polynomial test function φhand approximate solution Uh,the DG spatial discretization is performed as

where Ωvdenotes one particular cell in the computational domain,while ∂Ωvdenotes its boundary. The flux term F(Uh,∇Uh)˙n can be treated in exactly the same way as in the finite volume method. Specifically,the local Lax-Friedrichs(LLF)flux is adopted in this paper.
it has been revealed by many[29-30]that an accurate expression of the wall surfaces would have crucial influences upon the final accuracy in the DG method. Therefore,a mesh agglomeration approach developed by Qin[31]is adopted. More specifically,several elements are agglomerated into one highorder finite element cell,thereby acquiring a highorder approximation of wall surfaces. Such approach has been proved to be both very effective and efficient.
1.3 Time integration
Since the governing equations have already been reformulated in the rotating frame,many complicated periodical rotor CFD problems become steady - state problems[1,6,24]. Eventually,the discretized Eq.(17)can be rewritten as a set of ordinary differential equations on time t
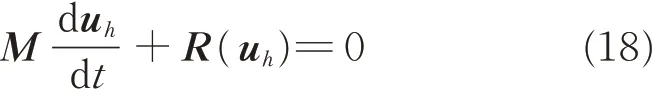
where M,uhand R denote the mass matrix,the solution vector,and the residual vector,respectively.
By using the backward Euler's formula,a difference scheme is then obtained

where Δuh=and Δt denotes the time step. Here we should notice the mass matrix M remains a constant matrix during the computational procedure,as there is neither motion nor transformation of the mesh in the rotating frame of the reference.
Let matrix A denote the Jacobian matrix of the LHS on U,and Eq.(19)can be solved by introducing Newton's method

Here the well-known block Gauss-Seidel method is adopted,namely
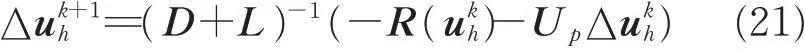
where D,L and Uprepresent the diagonal,lower and upper matrices of matrix A, respectively.Eq.(21)is applied iteratively until either the iteration number m meets a maximum or a given convergence tolerance is reached. in our simulations,Δt in Eq.(19)is gradually increased for the sake of faster convergence courses.
1.4 Modification of the boundary conditions
it can be distinctly noticed that since the governing equations are re - established in a rotating frame of reference,the boundary conditions should be modified accordingly.
1.4.1 Wall boundary
As the fluid has no viscosity,the wall surface is not able to generate force acting on the fluid along its tangential directions,but neither can the fluid penetrate the wall surface. in other words,the fluid and the wall surface should share the same normal velocity,namely

or expressed in the rotating frame

Therefore,the wall boundary condition in the rotating frame can be established. Similarly,the wall boundary condition is then recast in terms of absolute-velocity V
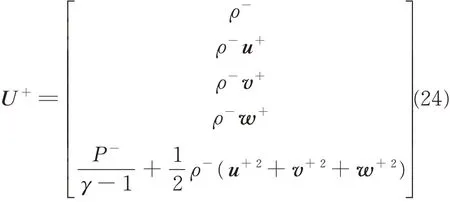
where Vrn=Vr˙n,u+=u--Vrnnx,v+=v--Vrnny,w+=w--Vrnnz. Variables with superscript“-”denote values from the inner elements,while variables with superscript“+”represent values of the boundaries.
1.4.2 Far-field boundary
One of the typical physical features of the hovering rotor flow-field is that the tail vortices and the down-wash flow induced can occupy a large distance of area blow the rotor hub. To reduce the amount of calculation due to the huge far-field range,Srinivasan[25]suggested a modified Jet-Sink boundary condition in 1992 which allows much smaller domains and has been adopted widely[1,10-18,24].
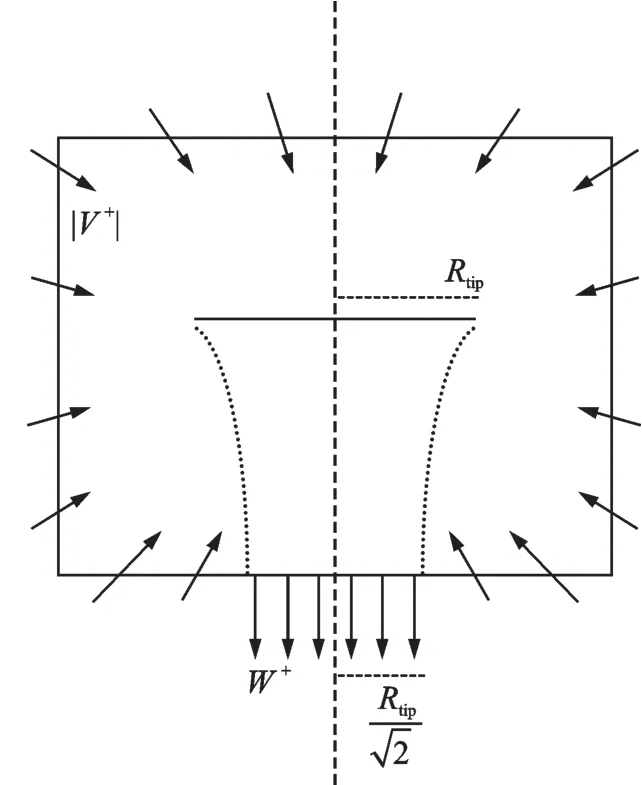
Fig.2 Jet-Sink boundary condition[24]
Such Jet-Sink boundary condition is modeled by a 3-D sink combined with a jet flow. As shown in Fig.2,assuming that there is a point sink centered at the rotor hub,sucking flow inside from all around except for a small area on the bottom boundary.The radial inflow velocity induced by the sink is defined as

where Matipstands for the rotor tip Mach number,Rtipand r are the radius of the rotor and the distance from the corresponding far-field boundary point to the rotating axis,respectively. CTrepresents the coefficient of thrust,which is proved to be an insensitive factor in this issue[6,25]and can be either the experimental data or the updating computational data.
As mentioned above,a circular domain of radius Rtip/right below the rotor hub at the bottom boundary is set to be the outlet for the jet flow. The jet flow is vertical and its speed is given by

Specially,for the DG method,the interface of the inflow and outflow at the bottom area may be contain in the same cell,which in other words would mean a small jump in speed that cannot be expressed by polynomial functions. Though the discontinuity is small and would not compromise the convergence or stability like shock waves,nonphysical oscillation and bad solution near the outlet is inevitable,especially in higher-order cases. Hence,a simple smooth procedure for the vertical speed inspired by Modisette[24]is developed in this paper.

Let wiand wodenote the vertical components of inflow and outflow velocities,respectively. The jet speed is redefined in the 2Δ range as

When setting Δ=0.1 R,wi=1.0 and wo=-1.0,the distribution of outer jet speed at the outlet is shown in Fig.3.
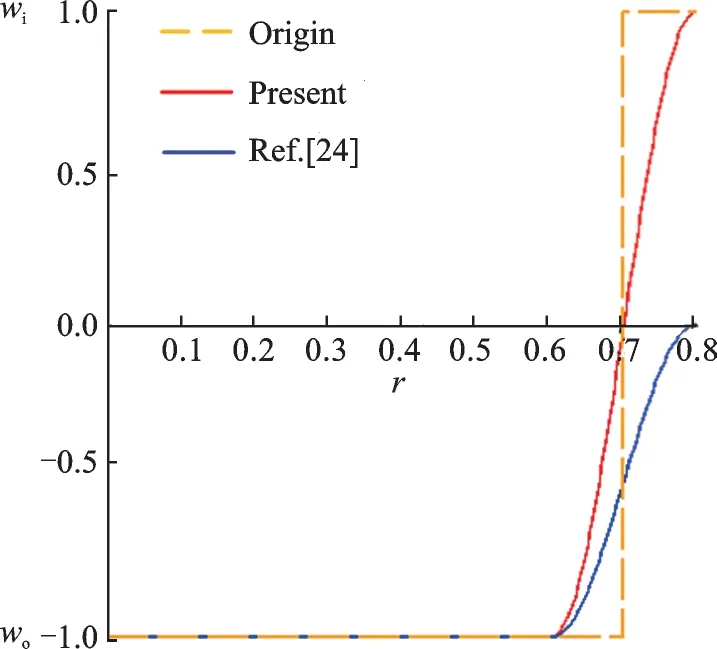
Fig.3 Jet speed distribution curves
The discontinuity is hence theoretically eliminated,but the outflow area is consequently larger in radius as well. However, experimental data[32]shows that the outflow area should be approximately 0.78Rtipin radius,which is slightly larger than the theoretical radius;hence our smooth approach could be more reasonable in this respect. Also,such smooth procedure can be employed in other methods like FVM without any modification.
The isentropic relationships between the flow at the outer boundary and the stagnation flow at infinity are used to specify the pressure and density.All these external variables are calculated by the well-known non-reflecting boundary condition.
However, Strawn and Ahmad[1]proposed that,the prescribed jetspeed in the Jet-Sink boundary condition could be combined with that of interior domains through two approaches at the outlet. The first approach,which is extensively used,is to apply the prescribed velocity directly(vertical speed restriction but pressure is restricted consequently).While the second way is only prescribing the external pressure through the velocity information and isentropic relationships (pressure restriction only).They believed that the second approach is more physically-realistic. However,the first approach is much more extensively used today[1,10-18,24],while the second is very rare to zero to be seen used[1].
To find out the specific difference among these two approaches and the common outer boundary conditions,both boundary implementations along with our smooth procedureand the common non-reflecting boundary condition are adopted and compared in our work.
2 Results and Discussion
The higher-order DG method istested by the case of the well-known Caradonna-Tung rotor in hover[27],for which Matip=0.439 and θc=8°.The primary goal of these experiments is to validate the higher-order DG method'sbetter performancein computing the thrust of the rotor and capturing the tip vortex effectively and accurately with much fewer unknown variables.Also,we are interested in the performance of different implementations of the Jet-Sink boundary condition and our smooth procedure;hence the test cases in our computations are categorized into four different types shown as below in Table 1.

Table 1 Descriptions of outer boundary conditions
As shown in Table 1,the smooth procedure is also adopted in the C-P case,but the influence is minor as the exit speed is naturally smooth in this case,but it can serve as a tool to adjust the outlet radius in this case.The common non-reflecting boundary condition is also adopted herefor further comparison,which would however demand a larger far-field range along the vertical direction in turn. in our work,a grid with large far-field range is generated,and then cut into a smaller one in the vertical direction for the Jet-Sink boundary conditions,so that all calculations in this paper would share the similar grid structure.
2.1 Grid configuration

Fig.4 Grid used for computations
The global view of the large grid utilized in our work is presented in Figs.4(a),(b),which contains 185 632 hexahedral elements and the geometric range is z=[-13.3 × Rtip,5 × Rtip] and r=[0,4 × Rtip](in cylindrical coordinates),where Rtipdenotes the wingspan of one single blade.The range of the smaller grid is tagged by the red lines in Fig.4(b),which is z=[-3×Rtip,2.8×Rtip]. This smaller grid contains 154 272 hexahedral elements,which are 17% fewer. The blade surface is divided into 20 segments along the span and another 20 along the chord,as can be seen in Fig.4(c). it is noticeable that all grids utilized here are much coarser than the others'[10-12],and therefore wall boundary approximation methods[31]are necessary.
Most calculations presented in this chapter are performed using p=3 DGM(4th-order accuracy)parallelly with 112 cores,while p=4 DGM(5th-order accuracy)solutions are calculated only for case FAR and case C-P.
2.2 Loading distributions
Fig.5 provides the pressure contours(p=3)on slice r/Rtip=0.68 and slice r/Rtip=0.89. The pressure distributions are fairly smooth and reasonable on such coarse meshes,indicating the effectiveness of high - order methods. in addition,the vertical speed contour at vortex age 45° is presented in Fig.6. Mild disparity between our result and the reference can be observed due to the absence of viscosity,but still the agreement is good overall.
Fig.7 illustrates the distribution of the pressure coefficient Cpalong the span and chord. The agreement between the numerical results and the experimental data is good in general,though with the absence of viscosity. The data shows that the DG method performs well in computing the thrust data accurately on relatively coarse grids. However,there are some discrepancies near the leading edge at the blade tip,which can also be observed in other Euler simulations[2,25].
2.3 Tip vortex capturing
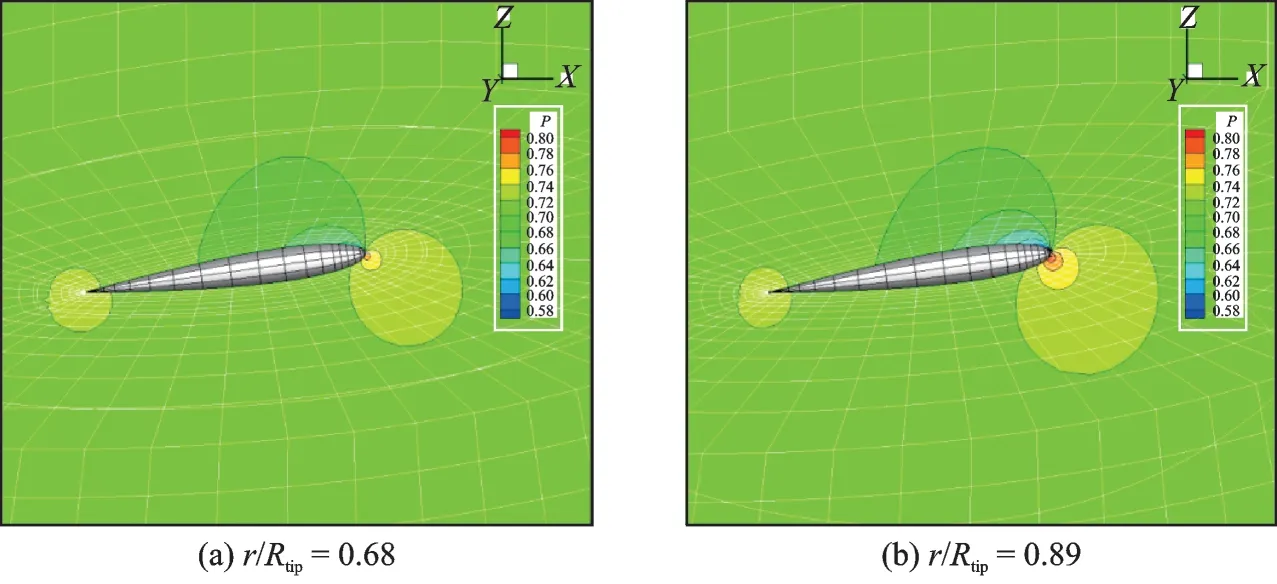
Fig.5 Pressure contours on different slices (Case FAR,p = 3)

Fig.6 Vertical speed contour at vortex age 45°

Fig.7 Cp distributions on different slices (p = 3)
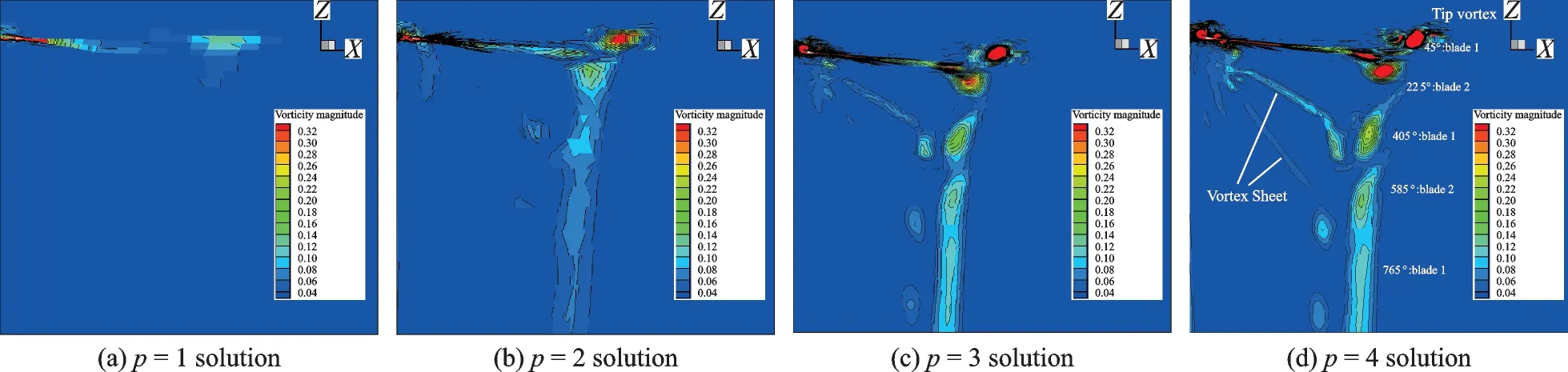
Fig.8 Local view of vorticity contour at vortex age 45°(Case FAR)
Fig.8 presents a closer look of the vorticity contour at vortex age 45°(FAR,p=1,2,3,4). it can be clearly seen that the solution gradually becomes clear and accurate as the polynomial order increases. in Figs.8(c),(d),five tip vortices along with several vortex sheets can be observed clearly.Comparing with p=3 solution,p=4 solution could yield a clearer capture of the tip vortices and the vortex sheets,and the vorticity magnitude is better preserved as well,yet p=3 solution is already accurate enough for the analysis. More specifically,the comparison between the numerical vortex core distributions and the experimental data is presented in Fig.9. Excellent agreement can be observed,except that both distributions stand very slightly below the experimental data. This might be the consequence of the absence of viscosity,which would otherwise slow down the descending and contraction process of the wake. Meanwhile,it can be learned from the excellent agreement that the viscosity exerts more influences on the transportation and diffusion rather than the generation of the strong wake system.

Fig.9 Radial and vertical distribution of the vortex core(p=3)
The iso-surface of vorticity in case FAR is presented in Fig.10. it can be seen evidently that at least 585° of the tip vortex is captured clearly.Fig.11 displays the iso-surface of entropy obtained from the FAR case in order to compare with the results presented in Ref.[25]. Through such expression,at most 765° of the tip vortex can be observed clearly,while the total degrees of freedom of this case are only 3 712 640(p = 3).

Fig.10 iso-surface of vorticity
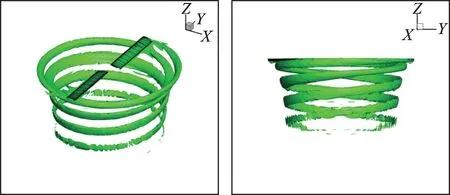
Fig.11 iso-surface of entropy
As listed in Table.2,Shaw et al.[10]captured clearly 450° of the tip vortex(displayed by vorticity)using a finite-volume discretization with around 4 000 000 DoF and a proper adaptation method based on the analytic description of the tip vortexpath,while 585° of the tip vortex is captured by using fewer amount of variables. This indicates that high-order method is much more effective in capturing the wake than traditional lower-order methods even with locally refined grids. As a further comparison,Modisette et al.[24]captured 630° of the tip vortex(displayed by entropy iso-surface)using the similar DG discretization with 2 524 710 × 2 DoF(p = 2 solution)and an output-based adaptation method. Comparing to our p = 3 solution with fewer DoF and without grid adaptation method,it can be seen clearly that the tip vortex is better preserved and captured through the higher-order method rather than locally increasing the element density. Either way our results suggest that higher-order method shows a better performance in capturing the complicated wake system using fewer DoF.

Table 2 Comparison of degrees of freedom (Case FAR,p = 3)
Further,the iso-surfaces of Case FAR p = 4 solution are presented in Fig.12. As can be seen in Fig.12,through both expressions the wake is captured about 180° longer and the magnitude is also better preserved comparing with p = 3 solution presented in Figs.10,11. This indicates that simply increasing the polynomial order in DGM is very effective in simulating the complicated vortex flow.

Fig.12 Case FAR higher-order solution (p=4)
2.4 Performance of different outer boundary conditions
it is interesting to notice that in Figs.7,9,the loading distributions and vortex core distributions obtained using different outer boundary conditions have barely any difference,which suggests that the outer boundary conditions have limited influences on both the thrust computation and the tip vortex capture near the blades.

Fig.13 iso-surface of vorticity
However,a circle of vorticity iso-surface is observed near the outlet in the C-W-Nons case in Fig.13,while it does not exist in Fig.10 in the FAR case. For further investigation,the vorticity contours of these four different outer boundary types at vortex age 0° are presented in Fig.14. As can be seen clearly,within the range of twice the wing span of the blade below the rotor hub,the vortex distributions seem to be all very similar,whereas in the area near the outlet at the bottom,the vorticity contours obtained with different outer boundary types are diverse. in the FAR case(Fig.14(d)),the vorticity could exit smoothly and straightly,while in the C-W-Nons case(Fig.14(a)),the vorticity is suppressed and concentrated near the outlet,and along the radial direction a large area is affected,which is consistent with the iso-surface data mentioned above. Strawn and Ahmad[1]reported the suppressed swirl velocity near the bottom when using this boundary condition as well. in the C-W case(Fig.14(b)),the vorticity magnitude near the exit is reduced significantly and the affected area is hence smaller in size owing to the simple smooth procedure.While in the C-P case(Fig.14(c)),no vorticity concentration is detected,and the vorticity can exit freely and smoothly. However,the shape of the wake is mildly malformed near the outlet in this case. The reason for this is still under investigation,but we suggest that a larger outlet radius is necessary.

Fig.14 Vorticity contours (p=3)

Fig.15 Entropy contours (p=3)
The distributions of entropy are also studied and found to be much more sensitive to the outer boundary types. Fig. 15 demonstrates the entropy contours obtained with different outer boundary conditions at vortex age 0°. in both the C-W-Nons(Fig.15(a))case and the C-W(Fig.15(b))case,the entropy seems to be forced to mainly distributein several plates along the vertical direction.And the closer to the outlet the plate is,the lager in magnitude the entropy is.
According to the analysis of the vorticity and entropy contours,we believe that in the ordinary Jet-Sink boundary condition the induced down-wash flow is unable to exit the flow-field freely due to the strong speed restriction. A part of the down-wash flow is hence reflected back by the inlet flow,and a large circle vortex ring around the outlet is then built up. Though small in magnitude,such vortex can exert a global impact on the flow-field.
in the C-P case(Fig.15(c)),when the speed restriction is removed,the entropy distribution becomes more reasonable and more similar to the clean and neat FAR case. Though it seems that more tip vortices are captured in the C-P case,the entropy iso - surface shape becomes circles rather than spiral lines after vortex age 630°. Also,a small area of entropy concentration near the outlet can be detected. These indicate that the gap between the CP case and the Far case is still significant.
However,for the C-P case when the spatial discretization accuracy is increased(p = 4 solution),as shown in Fig.16,both vorticity and entropy distributions become clean and neat while the influence of the outlet seems to be limited within a smaller range near the outlet.

Fig.16 Case C-P higher-order solution (p=4)

Fig. 17 Vertical speed distribution curves at the outlet(p=3)
Further,the line graphs of vertical speed distributions at the outlet plane(z=-3 × Rtip)are presented in Fig.17,so that we could study the influences of different outer boundary types more precisely. in Fig.17(b),severe oscillation is detected at the interface of inflow and outflow without the smooth procedure,while such oscillation is effectively restrained in the C - W case;besides,the smooth procedure manages to maintain the shape of the speed distribution curve. However,the difference between these two boundary types and the FAR case is significant in Fig.17(a). it can be evidently seen that the C-P case actually matches the FAR case better in terms of curve shape,though the W speed from the FAR case is consistently higher. in addition,the discontinuities in the velocity field are eliminated entirely in the C-P case. The radial range of the FAR case's outlet speed is also slightly lager,so we believe that it would be reasonable to further enlarge the outlet radius in the C-P case as mentioned above.

Fig.18 L2_norm residual convergence history (p=3)
The L2_norm residual convergence history(p = 3)of the Jet-Sink boundary condition implementations is presented in Fig.18(a). All calculations in these cases are initialized using the same initial values(C-W,p = 2 solution). in all cases the residual could converge quickly within 250 time steps,indicating the implicit DGM's excellent convergence and stability performance in higher-order cases. and with the simple smooth procedure,the residual could drop slightly lower than the original condition as we expected. it is also noticeable that the residual of the C-P case is consistently the lowest. Over all,we believe that the prescription of pressure only(the C-P case)is the most physicallyrealistic of the three Jet-Sink boundary condition implementations,which agrees with Strawn and Ahmad's conclusion in 2 000 as well. So we suggest that the rarely adopted pressure should be the preferable choice when using the Jet-Sink boundary conditions.
Fig.18(b)displays the L2_norm residual convergence history(p = 3)of the FAR case. in this case,more time steps are required to converge due to the much larger far-field range,and much smaller time step gap is necessary for the sake of stability. it is noticed that the residual fluctuates drastically between time steps 250 and 300. The possible reason for this might be that the L2_norm residual is supposed to indicate the convergence status of the global flow-field,whereas the elements far below the rotor hub(around z=-10 × Rtip)in this case are too coarse to capture too complicated flow structure.But the fluctuation is soon eliminated by the numerical dissipation on the large-scale elements and the global residual then quickly converges to around 10-4. This on the contrary demonstrates the stability and robustness of the DG method and the codes.
Overall,all boundary implementations have a limited influence near the blade surface,but the influences on the outlet and the global flow-field are significant and diverse. Common non - reflecting boundary condition could obviously yield the best results but the size of the grid and calculation is huge,while the Jet-Sink boundary conditions could yield reasonably good results for the engineering applications. in this respect,the Jet-Sink boundary conditions are recommended. The simple smooth procedure is proved to be effective for the speed restriction,and it can also serve as a tool to adjust the outlet radius in both speed and pressure restrictions for further study.
3 Conclusions
(1)The high-order discontinuous Galerkin spatial discretization for Euler equations in a rotating reference frame developed in this paper is validated.Though using Euler equations,the results show generally excellent consistence with references. Numerical experiments and comparisons manage to illustrate the higher-order DGM's impressive performance in computing the loading distributions and capturing the tip vortex both effectively and accurately with much fewer DoF. Convergence history presented here shows the stability and robustness of the implicit high-order method.
(2)The detailed comparison with results from lower-order DGM and traditional FVM both with grid adaption proves that higher-order methods are much more effective in capturing the wake of rotors than locally increasing the grid density. We suggest that future advanced p-adaptivity should be developed.
(3)The outer boundary conditions have limited influences on the loading distributions and tip vortex capturing within the range of twice the wingspan of the blade below the rotor hub,but they have different influences on the outlet and the global flowfield. Though common non-reflecting boundary condition with huge computational demands could yield the best results,the so-called Jet-Sink boundary conditions are recommended for engineering applications. The simple smooth procedure in this paper is also proved to be reasonable and effective,and it can be adopted by other methods or the pressure restriction as a special tool as well. Further,restricting the pressure at the outlet(the C -P case)is proved to be more effective and should be the priority of choice when using the Jet-Sink boundary condition,which is in contrast to most researchers'choice that restricting the vertical speed instead.
Further research on applications of higher-order discontinuous Galerkin method in rotorcraft CFD will be conducted. Viscosity and turbulence models will soon be included,meanwhile more complicated blade-vortex interactions(BVi)and aeroacoustic analysis will be investigated as well.
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Damage Detection and Material Property Reconstruction of Composite Laminates Using Laser Ultrasonic Technique
- An Efficient Method for Local Buckling Analysis of Stiffened Panels
- An Adaptive Transmission Scheme for Deep Space Communication
- Experiment on Boiling Heat Transfer of Refrigerant R134a in Mini-channels
- Self-Sensing Test Method for the Temperature of Piezoelectric Stacks
- Effective Thermal Conductivity for 3D Five-Directional Braided Composites Based on Microstructural Analysis
