一种新的双电子积分的计算方法

辽宁省锦州中学 赵宇阔

一般来说，在单中心的双电子积分的计算中，采用如下的近似方式是一种比较常见的解决方案，即：

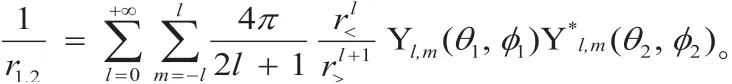
但是，在这种展开方式中存在着一种截断误差，特别是低轨道的时候，它的展开精度相对比较低。例如，在1s 轨道的计算中，它的计算精度为1 阶，即：。因此，除了Hylleraas 变分方法之外，其他的计算方法若不经过试验数据的拟合，其总能量的相对误差都将大于1.8%。

因此，为了解决这个问题，本文提出了一种新的计算方法，并且可以向任意阶展开。所以，本文的计算精度将优于上面的展开方式。

一、基本原理

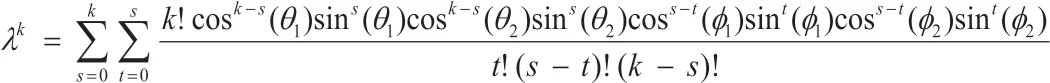
（1）。

设

那么根据式（1），可得：

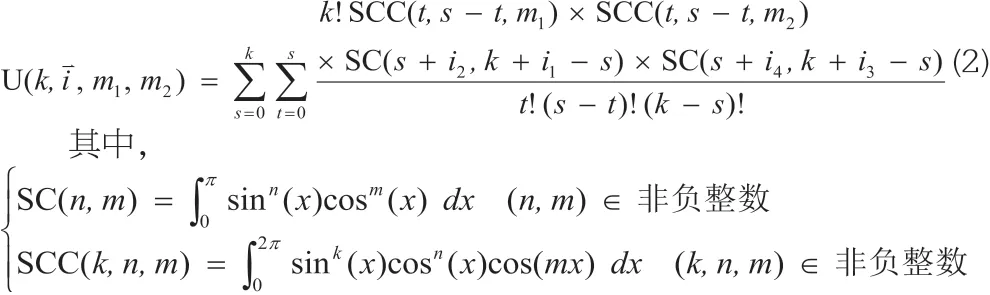
设

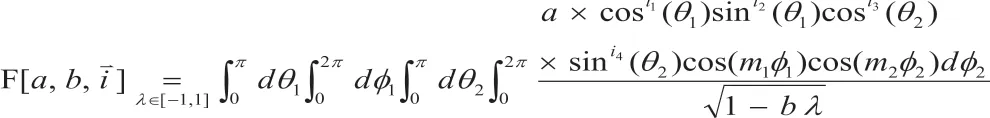
那么，根据式（2）和麦克劳林级数，可得：

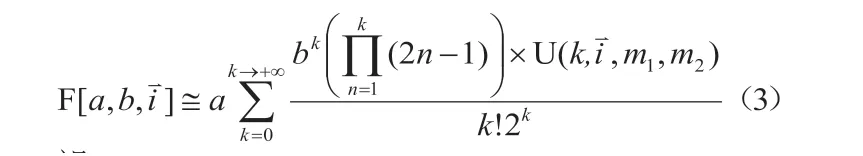
设

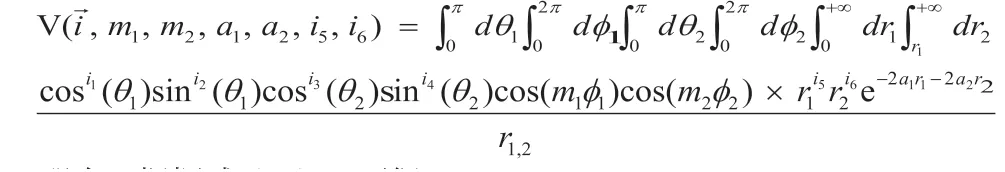
那么，根据式（3），可得：

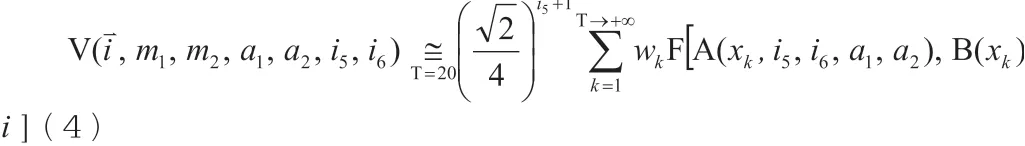
其中：

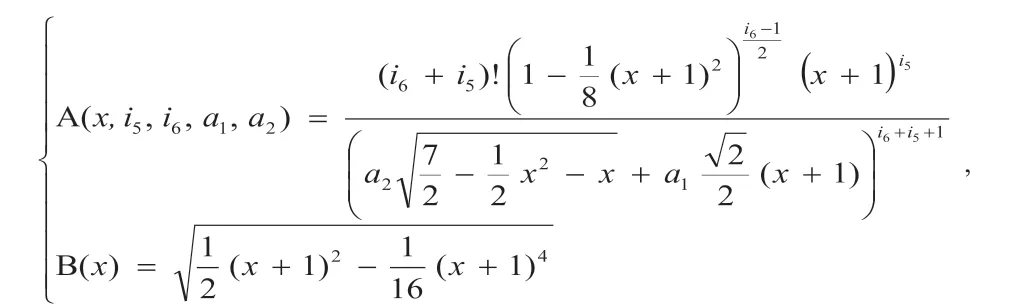
在定积分的计算中，由于高斯-勒让德积分可以向任意阶展开，所以，本文先通过积分变换，把一个六维的双电子积分简化为一个五维的定积分问题，然后再根据泰勒展开和高斯-勒让德积分的特点，从而获得式（4）的积分形式。并且，相对于文献1 来说，本文的计算精度要更高一些，但是时间复杂度却高于文献1。因此，在双电子积分的计算中，若是低轨道的积分计算，则建议采用本文的方法。否则，建议采用文献1 的方法。同时，有关这两种方法的结合使用，将是本文后续关注的一个焦点问题。