算法思想在初中数学教学实践中的研究

浙江省杭州市天杭实验学校 季晓霖

在数学课程标准当中，已经明确指出对于算法多样化的鼓励和推崇，虽然目前初中数学教学中还并未对算法思想的运用进行明确规定，但其应用的有效性已经得到呈现。教育现代化视野下，教学领域面临革新，迫切需要新的教学思想的融入和实践，从而为初中数学教学的健康发展提供保障，这既是教育领域的发展要求，也是教育现代化视野下出现的新内容。将算法思想与初中数学教学全面融合，对促进初中数学教学实效以及学生的全面发展将产生积极影响。

一、算法思想概述

1．算法思想内涵

目前学术研究领域对于算法思想的界定并无统一标准，表述方面存在显著差异，但从核心思想出发，其核心思想基本一致，即认为算法思想是一种解决问题的程序化、机械化的教学思想方法。

2．算法思想特征

算法思想本身具备以下几个方面的特征：（1）有限性。算法思想的应用需要在一个限定步骤之内结束，即通过算法在短时间之内解决问题，突出算法的有效性。对于“有限性”的解读，可以放在时间有限性和步骤有限性方面；（2）确定性。算法思想的应用，每一个计算步骤都需要确保准确性，避免发生歧义和模糊性因素。这一点与数学的核心思想保持较高的一致性，按照不同的步骤去执行和处理好各个步骤，最终输出相应的结果；（3）可行性。算法思想的应用，每一个步骤都需要保证可行性，并且能够得到被执行目标，在合理的范围内去输出结果；（4）有序性。算法思想在应用的过程中，需要按照严格步骤去具体执行，通过简单而机械的方式来得到答案；（5）通用性。算法思想的应用不仅仅是解决一个单一的问题，而是能够解决同类型的多个问题，具备通用性特点。总的来说，算法思想的基本特征赋予了算法思想独特性和应用价值。

3．初中数学教学中运用算法思想的教学目标

将算法思想运用到初中数学教学中，需要有一个明确的教学目标提供支撑。为满足数学教学的基本要求，确定教学目标如下：（1）能够接触自然的语言或者流程图来解决方程、函数以及几何知识点，并对于算法思想有一个最基本的了解，尝试运用算法思想来解决部分问题；（2）对算法思想有一个初步的感知，能够在独立思考当中去培养发散思维，实现思维层面的创新；（3）运用多种方法去解决问题，将算法思想应用到初中数学教学具体实践中，寻求解决方案的多样性；（4）在不断接触和运用算法思想的过程中，对算法的程序化、机械化以及通用化的特征有所掌握，全面感受和体会算法思想的内在价值和精髓。

二、算法思想在初中数学教学实践中的价值

1．培养初中生良好的思维习惯

从算法思想的内涵以及基本特征出发，将其应用到初中数学教学当中来，对于学生的思维习惯将产生重要影响。算法思想本身具备机械化和程序化的特色，对学生更好地掌握知识和技能具有积极作用，长期应用有助于学生自身形成条理化的思维模式。算法思想的应用，本身是由不同的结构组成，包括顺序结构、条件结构以及循环结构。人在思考的过程中，当面临复杂的问题和环境的过程中，需要从多角度着手，依据结构框架有一个清楚的认知，从而全面提高问题的解决效率。对于初中数学教学而言，算法思想的融入使得学生能够掌握科学的问题解决方法，完成一系列同类问题的有效解决，从而锻炼自己的思维习惯，对待问题本身有明确的条理性，逐步解决问题。

2．增强初中生数学思维能力

算法思想可以说是一种以解决实际问题为目的的高度概括的一个产物，算法本身就是一种逻辑顺序和逻辑条理的微观呈现，每一步处理程序、每一个过程都有明确的逻辑依据。将算法思想融入初中数学教学中，使得学生对于算法思想有一个基本的了解和认知，从而在数学思维能力的培养方面展现出算法思想的应用有效性。相比于固化的教学思想，算法思想的应用能够提高学生思维的灵敏度，探究一种全新的数学思维框架，对学生数学思维能力的培养将产生积极作用。总的来说，算法思想融入初中数学课堂当中来，对初中生的数学思维能力将产生积极影响，效用显著。

3．更深层次地接触和学习算法知识

初中阶段的算法思想，学生初步了解和感知即可。初中阶段的算法思想主要是增强学生的感知，去学习和接触更多的算法知识，从而为后续更好地应用算法思想奠定基础。虽然算法思想在初中阶段的应用是基础阶段，但也需要注意整个过程中学生对于算法思想的理解程度。在初中课堂当中，算法思想可以被融入各类型的课程教学中，为后续的学习奠定坚实基础。当然，算法思想想要在初中数学教学中发挥出应有的作用，并非一蹴而就，而是一个循序渐进的过程。初中阶段学生对于算法思想的理解和掌握程度，将对后续的学习产生深远影响。

三、算法思想在初中数学教学中的具体实践

1．算法思想在方程教学中的实践

在算法思想中，化归思想是其中的重要思想内容之一。化归思想在初中数学方程教学中经常被应用。例如在求解一元一次方程的过程中，具体过程涵盖了去分母、去括号、移项、合并同类项、系数化为1 的整个步骤；二元一次方程组求解，通常采取消元法和代入消元法；求解分式方程，多是要将其化为整式方程，然后求解、验根，得到方程的解。不同方程的求解过程，都体现了算法思想当中的化归思想。基于此，以分式方程为例，将算法思想应用到分式方程的求解当中，教学过程如下：

师：同学们应该都知道在一元一次方程的求解过程中，第一步是什么？

生：去分母。

师：解分式方程的第一步和一元一次方程相同，也是去分母。如分式方程，在求解过程中，则要联想一元一次方程的去分母过程，同学们还知道一元一次方程如何去分母吗？

生：方程两边同时乘以分母的最小公倍数。

师：如果分母中含有字母呢？

生：方程两边同时乘以最简公分母。

师：那这个分式方程的最简公分母是什么？

生：（x-5）（x+5）。

师：非常好，那么分式方程去分母之后，化为整式方程，现在得出的方程是什么形式？

生：x+5=10。

师：现在这个分式方程已经成为我们传统的一元一次方程，第二步则是求解方程，这个方程的解是多少？

生：5。

师：分式方程的分母不能为0，最后步骤则需要验根，将5 代入分式方程当中，看最简公分母是否为0？

生：为0。

师：这就说明这个方程无解。现在大家总结一下分式方程的求解步骤。

生：第一步，去分母，化为整式方程；第二步，解整式方程；第三步，验根。

在分式方程中将算法思想充分应用，能够让学生明白验根的重要性和为什么需要验根。相比于传统的教学模式，这种教学所展现出的效果更好，能够让学生初步感知算法思想，并运用算法思想来解决分式方程的相关问题。

2．算法思想在函数教学中的实践

函数内容是初中数学教学中的重要组成部分，算法思想在函数教学当中的应用实践，所展现出来的效果良好。为展现算法思想的应用价值，将其应用到一次函数教学当中来，设计教学方法如下：

师：当前，已知一次函数图像过点（3，5）与（-4，-9），求这个函数的解析式。

师：求一次函数y=kx+b 的解析式，关键在于求出k，b 的值，从已知条件当中可以列出有关于k，b 的二元一次方程组，并求出k，b，所以在这里我们首先需要做什么？

生：设函数解析式为y=kx+b（k ≠0）。

师：非常好，因为直线y=kx+b 过点（3，5）与（-4，-9），所以下一步要怎么做？

师：同学们回忆一下之前解方程组的步骤，下一步需要做什么？

师：最后我们根据这个结果，得出这个方程的解析式为y=2x-1。这种求函数解析式的方法被称之为待定系数法。对整个步骤进行总结，具体分为4 步：（1）设函数解析式；（2）列方程组；（3）解方程；（4）代入函数解析式。下面大家运用待定系数法去解决书中的课后练习题。

该教学案例则是将算法思想充分融入一次函数的教学当中，通过教师的有效引导，学生能够通过自身所储备的知识去解决问题，掌握使用待定系数法来求解函数解析式的算法思想。算法思想与实际问题的有效融合，对学生更深刻地理解算法思想具有积极意义。

3．算法思想在几何教学中的实践

算法思想在几何教学中的应用实践，以勾股定理的教学为例，其作为几何知识点当中的关键内容，勾股定理主要是表现三角形三边之间的数量关系，虽然内容看似较为简单，但该内容通常具有广阔的应用空间，在各个综合性的知识点当中均有所应用。将算法思想应用其中，如：已知△ABC 的三边长为a，b，c（a ＜c，b ＜c），判断该三角形是否为直角三角形，算法设计如下图所示：

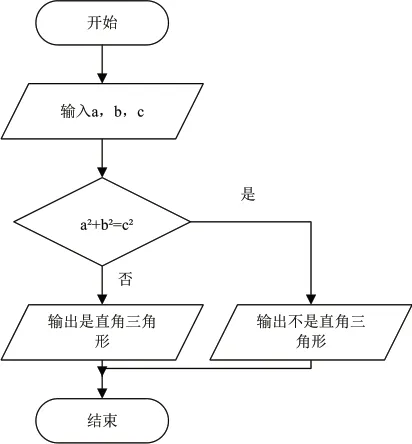
勾股定理的算法设计图

勾股定理的算法设计，结合教师的讲解，使得学生对于算法思想的认知度全面提升，通过该算法，用勾股定理判断直角三角形的过程更直观，学生对于算法知识的了解也更全面，所展现出来的效果更好。

四、算法思想在初中数学教学中的实践策略

算法思想在初中数学教学中的具体实践，将其分别应用到方程、函数以及几何知识点教学当中，所展现出来的应用效果显著，为教学实效性的提升以及学生更好地了解算法思想奠定了基础。但需要注意的问题是，想要算法思想发挥出更高的有效性，还需要制定实践策略，具体从以下几个方面着手：

1．渗透式教学

算法思想有效融入初中数学教学实践当中是一个相对漫长的过程，需要教师在开展教学实践的过程中，将这种思想渗透到教学实践中来，与数学教学内容充分融合。这样，学生在参与到数学课堂学习中时，则能够潜移默化地提升自己对于算法思想的认知度，从而在升入高中之后适应性得以全面提升。

2．算法化教学

相比于渗透式教学模式，算法化教学效果更直接。但还是需要借助渗透式教学模式，使得学生初步了解和掌握算法思想的内容。算法化教学则是对算法化的构造进行设计。在数学教学内容的选择方面，要做好筛选，选择具有典型代表性的教学内容，凸显出算法思想的机械化和程序化的特征，以算法构造为核心，在数学教学内容中充分展现算法的本质。

3．鼓励算法教学多样化

算法思想融入数学教学当中来，带来了数学教学发展新空间，使得数学教学别具魅力。算法教学的多样化使得教学内容更明确，对解决不同类型的数学问题具有积极作用。一方面，学生能够在算法教学多样化当中去提高解题效率和锻炼解题能力，另一方面，教师也能够在算法多样化当中提高自己的综合能力，走向专业化方向。可以说，算法教学的多样化，能够使得算法思想更好地融入数学教学实践当中。

4．强化算法教学与信息技术之间的关联

算法思想本身属于一种数学思想方法，与计算机科学之间保持着紧密的联系，算法思想与信息技术的完美融合，使得传统数学知识的解决方法更直观，效果更好。当然，将其应用到初中数学教学实践中，对学生学习兴趣的提升作用显著。

综上所述，初中数学教学对于学生的全面、综合发展具有积极意义。算法思想的融入，赋予了传统教学新的发展空间。借助算法思想，对于学生的综合发展将产生积极影响。同时，算法思想的融入，为学生后续的数学学习提供了诸多便捷性，值得全面推广应用。