单指令调度下堆垛机平均行程时间研究

王志珍

（西南交通大学 交通运输与物流学院，四川 成都 610031）

1 引言

与传统的仓库相比，自动化立体库具有很多优点，如节约了人力成本，加强了库存控制，提高了空间利用率。但是，自动化立体库建设成本高，在建设前必须对立体库进行合理的规划设计。结合自动化立体库的作业特点，在设计时需考虑多个关键因素，如堆垛机的数量、堆垛机的运行速度（水平和垂直方向）、货架排布方式等。相关资料表明，堆垛机的相关费用占自动化立体库建设成本的40%以上。从成本的角度出发，与堆垛机相关的因素在设计时应当优先考虑。

堆垛机的行程时间既能体现堆垛机的性能又能反应出立体库的布置是否合理，所以它是确定自动化立体库最优设计和调度的主要因素。在现有的研究成果中，Hausman，Graves和Schwarz[1]假定货架呈正方形并着重研究了不同存储作业规则下的单通道的行程时间模型；Bozer和White[2]对Hausman等人的研究成果做了进一步拓展，他们改变了货架的形状、输入/输出位置，得到了侧重点不同的单通道行程时间模型；Hwang和Lee[3]提出了基于堆垛机作业特征的行程时间模型。但是，这些研究都假定了堆垛机的运动状态是匀速运动的。从实践的角度来看，基于匀速运动构建的行程时间模型对于优化设计过程意义不大。基于单指令和随机存储策略，本文提出了综合考量堆垛机作业特征的匀加速运动状态的平均行程时间模型，为自动化立体库的设计和调度提供参考。

2 运动模式描述

堆垛机在自动化立体库中的运动包括水平方向和竖直方向的运动。每个方向的运动分别包括两种运动模式。为了描述这两种模式，现给出一些符号用以表征运动过程。堆垛机的加/减速度a，在任意时刻t速度为v(t)，最大速度vmax，在时间段t内移动的距离d(t)，达到峰值速度v(tp)需要的时间tp，到达指定目的地需要的总时间T。两种运动模式最大的区别在于堆垛机的峰值速度是否小于最大速度。

2.1 type1：峰值速度小于最大速度

第一种运动模式如图1所示，运动的相关表达式为（1）、（2）。

图1 峰值速度小于最大速度

2.2 type2：峰值速度等于最大速度

第二种运动模式如图2所示，运动的相关表达式为（3）、（4）。

当tp=T-tp时，堆垛机的峰值速度v(tp)恰好在tp时间点瞬间达到最大速度vmax，只是在(tp,T)时间段内堆垛机并未进行匀速运动，而是进行了与(0,tp)时间段内的运动相对称的匀减速运动。用l(t)表示堆垛机的上述运动状态，即堆垛机达到最大速度vmax时需要行走的最短路程。l(t)对于导出行程时间表达式具有重要作用，根据行程时间表达式可以确定该段行程的运动模式。l(t)的相关表达式为公式(5)、（6）。

图2 峰值速度等于最大速度

3 行程时间分析

为了确定行程时间模型表达式，提出以下假设：（1）货架为连续的矩形拣选面且I/O点位于最左端；（2）堆垛机基于单指令的调度，每条巷道一台堆垛机，作业于两排货架；（3）堆垛机的规格（水平和竖直方向的最大运行速度、加/减速度）以及货架的长度、高度已知；（4）接到调度指令时，堆垛机水平和竖直方向上的运动是同时进行的，且水平方向的最大速度不小于竖直方向的最大速度；（5）货架有足够的长度和高度从而保证堆垛机从I/O点出发能在水平和竖直方向上达到最大速度；（6）作业方式基于随机存储策略，即在货架的矩形拣选面上所有储位被选定进行仓储、拣选作业的概率相等。自动化立体库的排布方式如图3所示。

为了进一步刻画运动状态，用vx表示堆垛机在水平方向上的最大速度，vy表示竖直方向上的最大速度，a表示加/减速度（运动过程具有对称性，加减速度数值相等，方向相反），L和H分别表示货架的长度和高度，l和h分别表示堆垛机达到vx、vy时所需行走的最短长度和高度。

图3 自动化立体库排布图

考虑堆垛机不同运动模式的影响，水平方向的运动模式和竖直方向的运动模式将货架的矩形拣选面分为了4个区域，如图4所示。例如，type1,2表示水平方向的运动模式为type1而竖直方向的运动模式为type2。

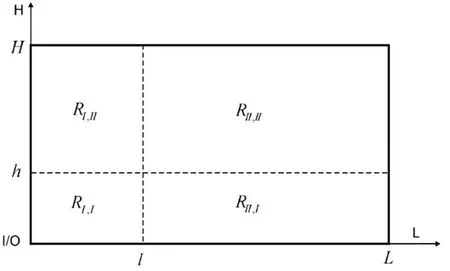
图4 仓储货架的四个不同区域

此外，以每条巷道的I/O点为坐标原点，用(xk,yk)表示任一货架储位（拣选位）k的坐标，其中0≤xk≤L，0≤yk≤H，txk表示堆垛机到达位置k水平方向的行程时间，tyk表示堆垛机竖直方向的行程时间，txk和tyk关于行程的表达式分别记作g(xk)、g(yk)。Tk表示堆垛机从(0,0)到(xk,yk)的行程时间，Tk=Max(txk,tyk)=Max(g(xk),g(yk))。联立方程(1)、(2)、(3)、(4)并求解得到关于 tx=g(xk)、ty=g(yk)的表达式(7)、(8)。

上述两组方程(7)、(8)表征的是水平和竖直方向上基于路程变量s的时间关系t(s)，因两组方程相似，做出可以代表水平方向和竖直方向运动的时间和路程的图像，如图5所示。

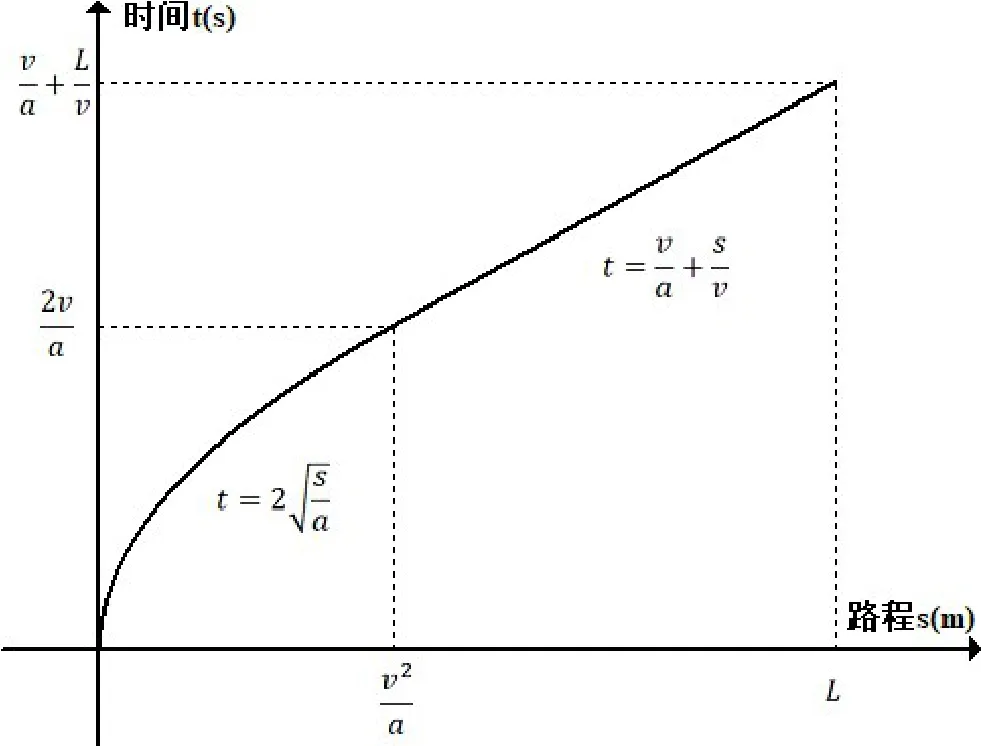
图5 时间和路程的图像：t(s)

引入分布函数F(t)用以表征堆垛机到达指定位置(xk,yk)所花费的时间小于t的概率。

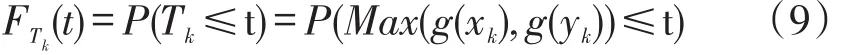
假定xk、yk相互独立，则水平方向和竖直方向的行程时间tx、ty也相互独立，表达式(9)可变形为以下形式：

FTk(t)=P(g(xk)≤ t,g(yk)≤ t)=P(g(xk)≤ t),P(g(yk)≤ t)（10）

通过分析可知，txk=g(xk)和tyk=g(yk)存在反函数，即g-1(txk)=xk，g-1(tyk)=yk，所以上述表达式可进一步变形为以下形式：

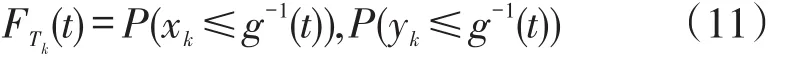
基于随机存储策略，可假定任意储位（拣选位）k的坐标xk、yk相互独立且服从均匀分布，因此：

式中g-1(t)表示的含义为堆垛机在时间t内行走的路程，即基于时间变量的路程关系 s(t)，则g-1(t)=s(t)，其图像如图6所示。

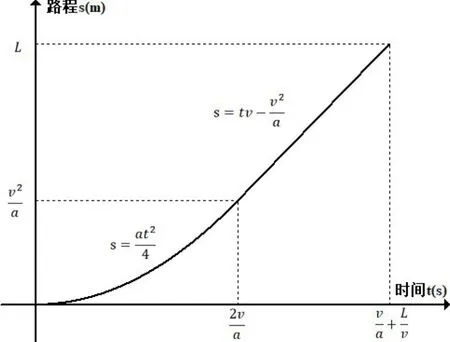
图6 路程和时间的图像：s(t)

基于上述分析，得到了关于Ftx

(t)和Fty

(t)的最终

kk表达式。

4 状态分析

通过对堆垛机行程时间的分析可知，行程时间t的分布函数FTk(t)的大小与 vx、vy、ax、ay、L、H 有关，基于前文的假设条件可以确定出三种不同条件下FT(t)的表达式。

在条件1下，FTk(t)的图像如图7所示。

图7 路程和时间的图像：条件1

在不同区间内FTk(t)的表达式为：

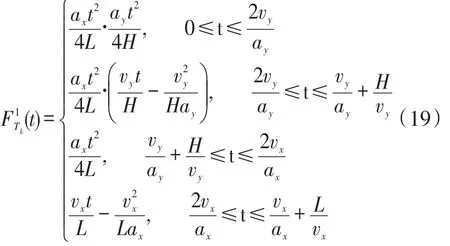
在条件2下，FTk(t)的图像如图8所示。

图8 路程和时间的图像：条件2

在不同区间内FTk(t)的表达式为：

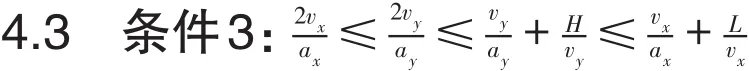
在条件3下，FTk(t)的图像如图9所示。

图9 路程和时间的图像：条件3

在不同区间内FTk(t)的表达式为：

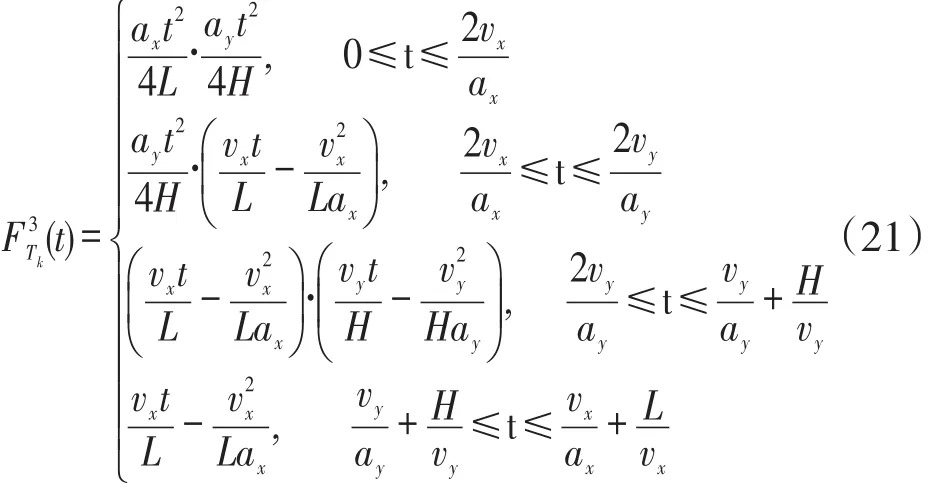
由于三种不同条件下的行程时间概率分布函数表达式已经明确给出，三种不同条件下的行程时间的概率密度函数 fTk(t)由此确定。用Em(OT)表示单指令调度模式下基于第m个条件堆垛机的平均运行时间，则其表达式为：

堆垛机在n(有限正整数)个运行指令下，到达的距离I/O点即坐标原点(0,0)最远的储位坐标为(x,y)，如图10所示，堆垛机在水平和竖直方向上运动的时间分别为Tx、Ty。则表达式（22）表示的含义为在以x和y为界构成的矩形作业区内，堆垛机在单指令调度下到达所有储位进行作业的平均行程时间。

5 分析与评价

为了评价构建的行程时间模型的准确性，在Flexsim中构建仿真模型，两种模型的vx、vy、ax、ay、L、H取值相同，通过对比分析两种模型的结果，对本文构建p模型的准确性做出合理评价。

定义货架长为60m，高为20m，同时假定每个货位长宽高都为1m。堆垛机水平方向的最大运行速度为5 m s，竖直方向的最大运行速度为2 m s。假定堆垛机水平方向和竖直方向的加/减速度大小相等，在仿真过程中考虑加/减速度大小不同的五种情况，取值分别为0.5 m s2、0.6 m s2、0.7 m s2、0.8 m s2、0.9 m s2。

Flexsim仿真模型和行程时间模型的计算结果见表1。从表1中的数据可知，在加/减速度不同的五种情况下，行程时间模型的计算结果与仿真模型得到的结果相比，最大的偏差只有0.161%。这充分表明，本文提出的行程时间模型的计算结果准确度高。因此，该模型在设计自动化立体库时能提供一定的参考价值。

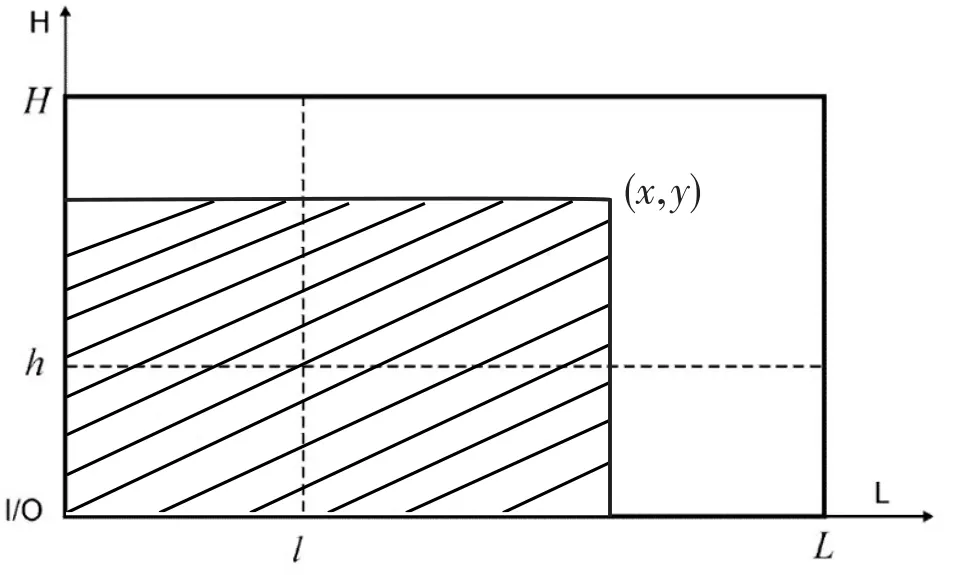
图10 有限个指令下最远储位示意图

表1 计算结果表

6 结论

堆垛机在自动化立体库中扮演着重要的角色，与堆垛机相关的指标对自动化立体库的绩效有很大的影响。本文以行程时间为切入点，提出了行程时间模型用以在自动化立体库的设计过程中提供参考，通过与仿真结果的对比，验证了模型在一系列假定条件下的准确性。

本文的平均行程时间模型是在堆垛机的单指令调度模式下提出的，但是实际生活中，还有双指令调度模式、一台堆垛机服务多条巷道模式等更为复杂的模式，表明文章的研究深度不够。此外，平均行程时间模型在很大程度上可以被视为评价模型。在自动化立体库设计过程中，该模型并不能直接给出堆垛机的最优运行速度、加速度以及货架的布局方式，只能在vx、vy、ax、ay、L、H这些指标确定的情况下给出较为理想的评价结果。本文假定了水平和竖直方向上的加速度数值相等的情况，没有对加速度不等的情况进行研究，也没有考虑堆垛机的变加速运动情况。