基于禁忌搜索算法的煤炭港口配装计划

皮幺梅，夏振喜，王维杰

（武汉理工大学 物流工程学院，湖北 武汉 430063）

1 引言

煤炭作为我国的基础性能源，是我国经济飞速发展的重要支撑。不同煤种在发热量、灰分、硫分、水分等特性上存在差异，其质量和对燃煤设备的损耗上也有所区别。为满足客户需求，需要将不同种类的基础原煤按照一定的比例混合后形成客户需求的合同煤种，这个混合过程就叫做配煤[1]。所需的原煤种类和比例称为配煤方案，构成合同煤种的配煤方案有多种。随着配煤迅速发展，配煤业务从煤炭生产企业和用煤企业延伸到了中转港口。但由于堆场空间和设备限制，配煤方案的选择和装船取料时垛位选择影响整个港口的场存情况，这种配装的不合理也导致船舶因缺少配煤方案所需的煤种而长时间在港等待。因此，煤炭港口配装计划是否科学将直接影响到港口的吞吐能力、船舶在港停靠的时间以及港口服务水平，进而影响到港口和货主的经济利益。而在我国煤炭需求旺季，港口经常出现煤炭场存供不应求的现象。因此，如何合理利用现有场存进行配装，最大程度地满足所有船舶需求是煤炭港口面临的一个重要问题。

堆场是储煤的场所，按照船舶需求，合理有序的配装是码头作业中的一个重要问题。众多学者分别从不同的角度分析煤炭港口的配装问题，并运用不同的数学模型和算法来表述和求解这类问题。Boland等[2]充分考虑到船舶煤炭需求、堆场资源以及时间的不确定性，通过综合优化泊位分配、堆料位置、装配开始时间三个方面来提高港口服务效率，建立了堆场动态调度模型，并提出了基于贪婪构架、枚举和整数规划相结合的新技术。Savelsbergh[3]等研究澳大利亚猎人谷煤炭链中港口配煤的煤炭装配问题，基于煤炭港口装配问题在时空图上显示的几何特性，提出了一种树搜索算法来最大化堆场的吞吐量。Wen等[4]则从另一个角度和方法阐述煤炭配装问题，将港口配煤装配问题转化成特殊顺序约束的二维装箱问题，建立了堆场动态调度CP模型。上述学者们的研究中，港口的条形堆场是连续型的，即配煤方案下煤种是连续堆放在一个条形堆场上。与之不同的是，我国部分大型的配煤港口条形堆场上的垛位是离散型的，每个垛位长度和堆放煤种是固定的，垛位堆放的是未经混合的基础原煤，如秦皇岛港。而针对这种情况下我国煤炭港口的煤炭配装问题研究很少。

禁忌搜索算法（Tabu Search，TS）[5]是基于领域搜索的全局优化算法，它通过模拟人类思维过程，利用禁忌表记忆局部最优解，达到跳出局部搜索的目的。在解决众多组合优化问题[6-7]上，TS算法较好地平衡了解的局部集中性和解的全局多样性问题，是一种局部搜索能力很强的全局迭代寻优算法。但是，TS算法对初始可行解具有较强的依赖性，好的初始可行解能够提高TS算法的搜索效率，而一个差的初始可行解则会影响TS算法的收敛速度[8]。

本文根据煤炭在煤炭港口的物流阶段，以垛位、配煤方案、合同煤种和船舶等以对象建立网络图节点，以对象之间的关系建立相应的边，用带特殊约束的网络流问题描述港口的配装问题，并建立配装计划的最大流模型。考虑船舶的优先级顺序，煤炭港口的配装问题是个带有优先级顺序的组合优化问题，本文设计了禁忌搜索算法，并提出了基于初始解的改进禁忌搜索算法。

2 配装计划的最大流模型

2.1 问题描述

在一定长度的计划期内，煤炭港口存在多艘待装船舶。船舶需求的是合同煤种，一艘船需要的合同煤种一般为一到三种。合同煤种对应的配煤方案是港口已知的，见表1，船舶v1需求的合同煤种为d1，d2两种。对于每种合同煤种，其配煤方案为多个。每种配煤方案由含比例关系的一到两种基础原煤组成。

表1 船舶v1需求的合同煤种对应的配煤方案

对于一艘船舶的一种合同煤种，可以同时选择多个配煤方案，即为此合同煤种的配煤方案组合，但每种配煤方案下的基础原煤取料数量需满足配比关系。并且，每种合同煤种对应的配煤方案组合下的总装船数量等于船舶对此合同煤种的需求数量。可以看出，不同船舶之间可能需求相同的基础原煤，即存在需求竞争关系。堆场堆存的基础原煤种类很多，由于地理空间和设备工艺的限制，垛位堆放的基础原煤只能被运输到可到达若干泊位上，依此，与相同堆场相通的泊位为同类泊位，划分为同一区域。与此区域的泊位相连通的条形堆场分为这一区域。例如，区域1内的泊位为泊位1、泊位2、泊位3，区域1内的堆场序号为1，2，3，4，5。区域1的煤炭只可运输到区域1内的泊位上。

假设堆场在该规划期内不会补充库存，已靠泊船舶不允许更换泊位，船舶之间存在服务优先级顺序，港口的场存优先满足高优先级船舶的需求。基于此，煤炭港口的配装计划是根据堆场堆存的煤炭种类和数量，泊位与堆场的可达性，计划船舶合同煤种的配煤方案组合，在满足配煤方案下煤种和配比要求的情况下，为船舶安排具体的取料垛位和相应的取料数量，以满足优先级顺序下的船舶需求。

2.2 最大流模型

设G=(N ,A)是有向网络图，N，A分别为网络图G中的节点集合和边集合。在本问题中，研究对象包括垛位、配煤方案、合同煤种、船舶，其属性见表2。按照对象属性，分别建立垛位、配煤方案、合同煤种、船舶节点及发点与垛位层、垛位层与配煤方案层、配煤方案和合同煤种层、合同煤种层和船舶层、船舶层与到收点之间的边。

网络图的符号定义如下：节点集合N={s,t}⋃Nm⋃Nl⋃Nd⋃Nv，其中，s和 t分别为发点和收点，Nm、Nl、Nd、Nv分别表示垛位层、配煤方案层、合同煤种层和船舶层的节点集合。Nv表示船舶v(v∈V)代表的节点集合，Nv∈Nv。配煤方案节点i的比例为ki，节点i的入弧左节点中（垛位节点），此配煤方案的第一种基础原煤c的节点集合为Nc1，表1i示基础原煤c的节点集合为Nc2。(i,j)∈A表示网络2i图中的有向边，i,j表示网络的两个节点,δ-(i)和δ+(i)分别表示节点i的入弧和出弧集合。uij表示边(i,j)上的容量，按照节点i,j表示的对象，分别为垛位堆存的煤炭数量、合同煤种需求、船舶总需求等。xij，yij为模型的两个决策变量，xij表示边(i,j)上的流量，0≤xij≤uij。yij表示边(i,j)是否连通,连通时值为1，否则为0，即yij∈{0,1}。则煤炭港口的装配网络流模型如下：

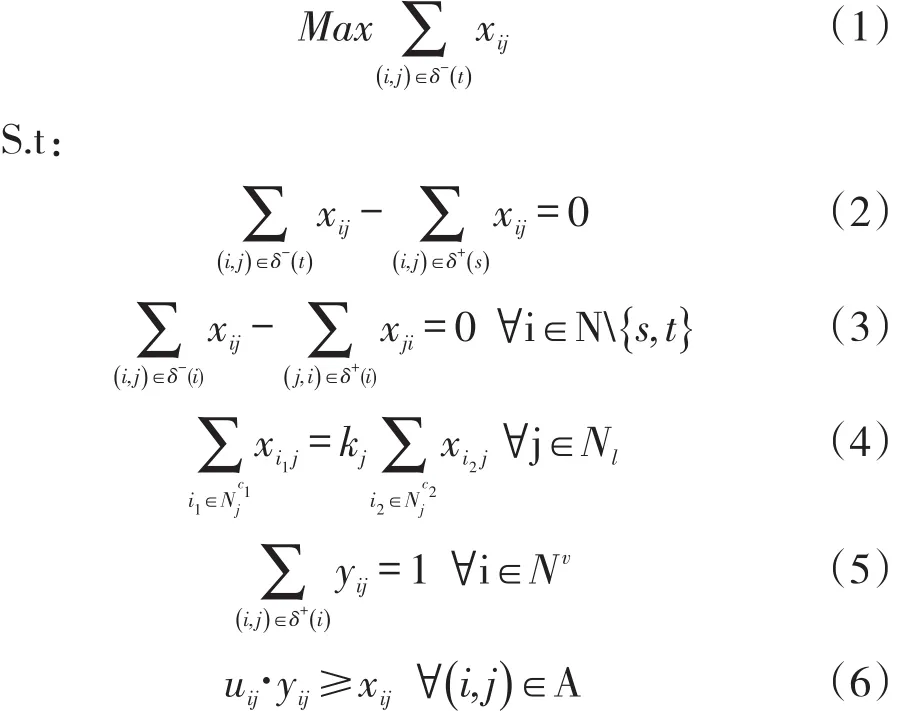
其中，式（1）表示目标函数，最大化网络总流量，即所有船舶的最大装船量之和；式（2）表示网络流入量等于网络流出量，即港口的总取料和总装船数量应相等；式（3）表示节点为发点和收点外的节点时，流出量等于流入量，表示单艘船舶的取料数量与装船数量应相等；式（4）表示配煤方案中基础原煤之间的配比约束；式（5）表示一艘船舶只能停靠在一个区域的泊位上；式（6）为容量约束，取料数量不得超过堆垛的剩余场存数量，且当弧是断开的时候，弧上流量为零。与一般的网络流问题[9]相比，上述的煤炭港口装配计划网络流是个带特殊约束的网络流问题，网络图中边流量带比例约束和节点带分流约束。

表2 对象及对象属性

3 禁忌搜索算法

船舶的服务优先级顺序是煤炭港口配装计划过程的重要考虑因素。在网络图G中，船舶的优先级顺序体现在船舶层节点Nv的出弧带优先级顺序，优先级高的节点应被优先通过最大流量。对于边含优先级顺序的网络流问题，可以被转化成边带权重的网络流问题，而随着边的个数增加，权重大小将呈指数型增长。为解决船舶含服务优先级顺序的配装计划问题，本文将其考虑为边含优先级顺序的网络流问题，并提出禁忌搜索算法及其改进。禁忌搜索的基本思想为：从一个初始可行解出发，选择一系列的特定移动方向搜索局部最优值，通过对局部最优解的禁忌，达到跳出局部搜索的目的，其有效的邻域变换实现全局优化。

假设船舶优先级顺序集合为P，船舶V={v1,v2,...,v||P}。优先级大小为 p的船舶vp在网络图G对应的节点集合为Nvp。定义最大迭代次数为T，每次搜索邻居的个数为Num，禁忌表JinjiArr，长度为Len。禁忌搜索算法的设置如下：

（2）邻域选择。邻域移动采用“节点变换法”，即对解空间中两个船舶的节点进行随机变换。随机选取两艘船舶vi和vj，从船舶vi和vj对应的节点集合中各随机选择一个不同的节点ni和nj，形成新的解空间 F'，如F'={n1…ni…nj…n|P|}。

（3）解集评价函数。将当前解集与当前最优解中船舶vp(vp∈V)的最大装船量进行一对一比较，当优先级高的船舶表示的点的出弧流量（船舶最大装船量）更高，则解更优。

（4）终止条件。本文采用“迭代步数准则”。当运行到步数T终止搜索，输出当前最优解集。

禁忌搜索算法过程如下，其中，Algorithm1为煤炭港口配装计划的禁忌搜索算法，Algorithm2为解集F的评价函数算法。

Algorithm1∶煤炭港口配装计划的禁忌搜索算法（考虑优先级顺序）Input：网络图G ，Nv||P(∀vp∈V)，初始解集 F0 Output：当前最优解集Fbest，解集下的节点最大流量集合MFbest Function：TS_Pr iority(G,F 0)初始化MFbest=φ，Fbest=φ MFbest=Maxflow(G,F 0)for t=0;t＜T;t++令当代最优解Flocal=φ，临时解Ftemp=φ当代最优解和临时解下的节点流量集合MFlocal=φ，MFtemp=φ for num=0;num＜Num;num++随机选取F 0的邻居Ftemp，若Ftemp在禁忌表，则重新选取Ftemp计算优先级顺序的网络最大流量，MFtemp=Maxflow(G,Ftemp)比较MFlocal与MFtemp若 MFtemp优于 MFlocal，则 MFlocal=MFtemp end for比较 MFlocal与MFbest若 MFlocal优于 MFbest，则 MFbest=MFlocal，Fbest=Flocal删除JinjiArr第一个元素，将Flocal加入禁忌表JinjiArr end for Algorithm2∶解集F的评价函数算法Input：网络图G，解集 F={n1…n||P}Output：每艘船舶在满足优先级顺序的最大装船数量集合MF Function：Maxflow(G,F)初始化：网络图G中的船舶层节点，得G'。令MF=φ for p=0;p＜ ||P;p++将np加入到G'，计算网络最大流下的节点np的出弧流量 flownp固定网络图G'中节点np的出弧流量 flownp ，更新G'MF=MF⋃{flownp}end for

禁忌搜索算法采用了禁忌技术，弥补了局部搜索算法可能陷入局部最优的不足，用禁忌表对已达到的局部最优解进行“记忆”。但是禁忌搜索算法对初始解的依赖性较强，较好的初始解能帮助算法更快的收敛，寻到全局最优。因此，本文提出了基于初始解的改进禁忌搜索算法。

改进的禁忌搜索算法思想如下：对于优先级p=1的船舶v1，若Nv1的元素个数则计算网络G中只含的节点，得出Nv1中流量最大的节点集合，则选出船舶vp+1对应的节点集合中优先级下的最大流节点N'，并令如此，通过对初始解的改进，达到加快禁忌搜索算法的收敛速度，继而改进禁忌搜索算法。

4 数值实验

本文选取三组不同规模的数据进行实验，见表3。A，B，C三组数据的船舶个数分别为10，20和30。每组数据的堆场垛位与船舶等对象构成的网络规模随着船舶个数相应增加。船舶集合中船舶的编号顺序即为船舶的优先级顺序。分别运用禁忌搜索算法和改进的禁忌搜索算法求解不同规模下的煤炭堆场配装问题。

表3 实验数据规模

本实验是在64位操作系统，英特尔双核2.30GHz的处理器，6G运行内存的个人电脑上完成，运用java语言编程，结合CPLEX求解器，运用禁忌搜索算法求解煤炭码头的装配计划最优解。令最大迭代次数为T=100，每次搜索邻居的个数为Num=20，禁忌表JinjiArr，长度为Len=20。以数据A1的求解结果为例，船舶v1的配装计划见表4。

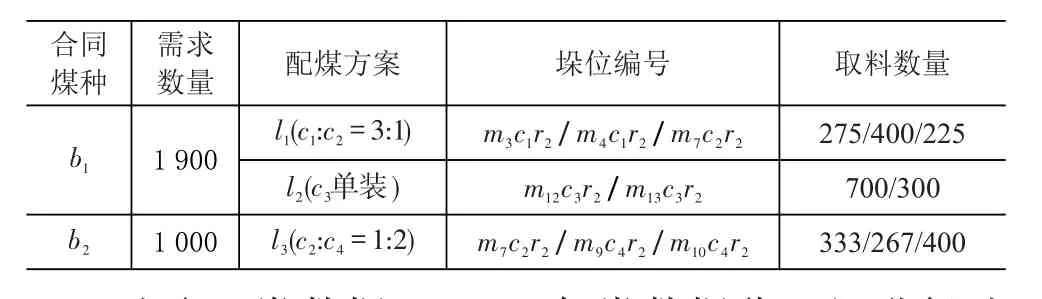
表4 数据A1下船舶v1的装船取料计划

选取三类数据A，B，C，每类数据分三组进行试验，结果见表5。通过对比可以得出，由于改进的禁忌搜索算法对初始解进行了改进，其改进的禁忌搜索算法略高于禁忌搜索算法。但是，9组不同规模的数据实验结果中，改进的禁忌搜索算法的最优解出现的代数要平均早于禁忌搜索算法最优解出现的代数。这表明改进的禁忌搜索算法的收敛速度要优于未改进的禁忌搜索算法，算法的改进是有效的。由于改进的禁忌搜索算法在进行局部搜索之前，需要进行初始解的改进，所以，在求解时间上略高于未改进的禁忌搜索算法。

表5 禁忌搜索算法与改进的禁忌搜索算法的结果对比

5 结语

本文根据大型煤炭装卸港口煤炭配装过程的多个物流状态，建立了煤炭港口配装计划的最大流模型，为煤炭港口的计划调度优化问题提供了新的思路。考虑船舶的服务优先级顺序，煤炭配装问题是个带优先级顺序的组合优化问题。本文设计了禁忌搜索算法求解这类带优先级顺序的组合优化问题，并通过对初始解的优化来改进禁忌搜索算法。最后，算例实验表明，改进的禁忌搜索算法具有较好的收敛性，可以较好地解决煤炭港口配装计划问题，对提高港口服务效率具有重要意义。