基于空间三角测距的激光雷达三维重建实验系统

陈梦雯，迟克浩，陈文娟

(中国石油大学(华东) 理学院，山东 青岛 266580)

三维重建[1-3]是指通过获取待测目标的三维数据，并通过软件对数据进行处理，使数据能够在计算机的环境下进行操作、分析，进而对待测环境进行虚拟重建的技术. 三维重建技术在管道巡检、遗址废墟研究以及地震灾区救援等方面发挥着重要的作用. 随着计算机视觉技术的高速发展，空间环境的三维重建方法也愈发多样化. 但目前市面上很多视觉技术方案，如单目[4]或双目视觉[5]等，较易受环境光线的影响，且成像精度较低. 因此，设计并制作三维重建实验系统，将抗干扰能力强、测距精度高的激光雷达[6]应用在对空间环境的三维重建[7-14]中. 该实验系统采用自主拓展的空间三角测距原理作为其测距成像的方法，相比传统的TOF(Time of flight)法具有制作成本低、操作简单、易于携带等优点.

1 激光雷达重建系统的成像原理——空间三角测距原理

1.1 单点三角测距原理

使用单点三角测距原理能够计算出点状激光照射到的空间任意一点到点状激光器的距离d，原理图如图1所示，测距公式为

(1)

其中，摄像头的焦距为f，固定摄像头和激光器的平面为s(可认为两者的中心距离为s)，x是待测目标的反射光在摄像头成像平面上所成的像到一侧边缘的距离，激光器发出的激光线与该固定平面s的夹角为β.

图1 单点三角测距原理图

1.2 单点测距公式的完善

在实际计算中，需要进一步结合扫描器和摄像头的实际结构对测距公式进行完善.

在系统安装完成后，整个系统中的相机坐标系、像素坐标系与图像坐标系的几何关系如图2所示，其中，相机坐标系的Xc轴与扫描器基准线平行.

摄像头中心点位于点Oc，摄像头的成像平面为平面ζ，待测物体的反射激光在摄像头的成像平面ζ上成像，对于不同远近的物体，其成像光点在成像平面的位置发生变化. 式(1)中的x表示了该位置的变化，是唯一需要获得的未知变量.x的含义是待测目标的反射激光在摄像头成像平面上所成的像到一侧边缘的距离.x值为

x=Xpx,

(2)

其中，px是反射激光点在摄像头成像平面上的像素横坐标，X是摄像头成像平面上单个像素感光单元的横向尺寸.

图2 相机坐标系、像素坐标系与图像坐标系几何关系图

由于式(1)和式(2)中变量x的原点位于Oo(摄像头成像平面上感光阵列的第一列)的概率非常小，所以，通过像素坐标px计算得到的x值与实际值存在一定的偏差量Δx，该偏差量可通过后文的参量拟合步骤求得. 变量的实际值应为

x=Xpx+Δx,

(3)

联立式(1)和(3)，得到通过激光光点像素坐标px求出距离值d为

(4)

1.3 线激光中心点的距离测定

对空间环境进行三维重建时，仅使用点状激光无法得到环境的3D数据，因此，使用红外线状激光器扫描空间环境，每次对一条扫描线上的各点进行测距，同时将扫描器旋转180°，实现对空间环境的三维扫描. 图3为系统扫描器的结构设计图.

图3 扫描器结构设计图

首先假设待测目标所在平面与摄像头成像平面ζ平行，并假设摄像头的成像平面ζ绕扫描器所在平面s翻转180°，得到摄像头成像平面的翻折面γ(以红色箭头表示翻折情况). 扫描测距过程中，扫描器所在平面s与摄像头的成像平面ζ平行，因而扫描器所在平面s与摄像头的翻折平面γ也平行. 绘制出线状激光照射在平行平面α上时，扫描器所在平面(视为基准线)s、摄像头成像平面的翻折面γ以及待测目标所在平行平面α的几何关系图如图4所示. 其中，平面α为待测目标所在平面，其上的紫色线条l1为照射在待测目标所在平面α上的线激光，l2为摄像头成像平面的翻折面γ上的线激光，l1与l2相互平行.

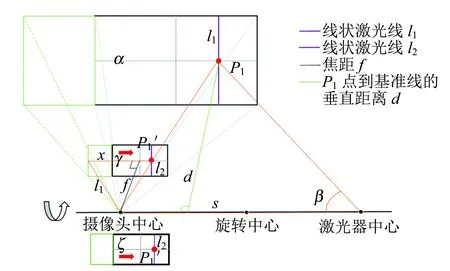
图4 平行平面上P1点实际距离求解的几何关系图

线激光线l1上的P1点位于激光线的中心位置，依据针孔摄像机的原理，该点在摄像头成像平面ζ上所成的点位于成像平面ζ的高度中点，所以，平面γ上的投影点P1′也位于平面γ的高度中点，P1′到基准线s的垂直距离为摄像头的焦距f. 结合图4，P1点到基准线的垂直距离d可以直接利用单点三角测距原理中的式(4)进行计算.

1.4 线激光任意位置的距离测定

本系统在对线条l1上的其他各点，如点P2的距离进行求解时，将单点三角测距公式拓展到空间，在使用式(4)求得距离d的前提下，利用三角形相似等定理，推导得到求取空间各点实际距离值的空间三角测距公式.

首先，根据式(4)求出中心点P1点到基准线s的垂直距离d，再求出平面γ上的俯仰角θ：

(5)

其中，h为平面γ的纵向长度.P1y′和P2y′分别为点P1′和P2′在摄像头成像平面ζ上的实际高度，但由于平面γ是通过将摄像头的成像平面ζ进行180°翻折得到的，所以P1′和P2′点在平面γ上的高度为h-P1y′，h-P2y′. 而P1y′和P2y′可由下式求得：

Py′=pyY,

(6)

其中，py为P1′或P2′在成像平面ζ上的像素纵坐标，Y是摄像头成像平面ζ上单个像素感光单元的纵向尺寸,则P2点到基准线s的垂直距离d′为

(7)

设P点为P1点和P2点到基准线s的垂线与基准线s的交点，则激光器中心点到P点的距离m为

(8)

根据勾股定理，可分别求出P1点距激光器中心点的距离d1为

(9)

P1点距扫描器中心点的实际距离dr1为

(10)

其中，r为基准线s的半长,

(11)

P2点距激光器中心点的距离d2为

(12)

P2点距扫描器中心点的实际距离dr2为

(13)

通过上述推导过程，能够得到与扫描器所在平面(基准线)s平行的平面上任意点到扫描器中心点(激光器中心点)的实际距离，而对于求解三维空间中任意某点的距离，可以过该点构造与扫描平面平行的平面，此时待测目标点即位于图5中线激光l1上的P2(P1)点，即可利用上述推导得到的空间三角测距公式(9),(10),(12)和(13)对距离进行求解.

图5 平行平面上P2点实际距离求解的几何关系图

2 实验系统装置设计

2.1 装置的硬件设计

本系统只需使用线状激光器和USB摄像头，配置简单的驱动电路，通过Arduino控制板控制舵机以及履带小车，并使用计算机软件进行图像处理，最终将设备安装完成并调试后，即可实现对待测空间的180°扫描重建.

装置的设计图与实物装置图如图6～7所示.

图7 实物装置图

线状激光器和USB摄像头构成装置的信息采集模块，分别放置在通过3D打印的固定平台的两端，平台下端固定在舵机转盘上并与舵机转轴相连，使用履带小车搭载信息采集模块、舵机以及Arduino控制板.

实验系统工作时，计算机将控制程序烧录到Arduino控制板中，利用Arduino控制板实现对舵机以及履带小车的控制，通过履带小车的运动以及舵机的转动，进而带动信息采集模块对待测空间进行180°扫描. 转动过程中红外线状激光器发射线状激光，USB摄像头对空间表面的反射光进行接收，并将信息发送给计算机，对信息进一步分析处理，实现对待测空间环境的三维重建.

为有效去除环境中杂光的干扰，装置采用红外激光器，并且去除摄像头中的红外截止滤光片，改为加装带通滤光片，仅允许激光器发出的980 nm波长的红外光通过. 因此，背景光的干扰几乎被除去，对摄像头画面上激光光斑的提取也更加快速准确.

2.2 装置的程序设计——线激光的光点坐标提取及点云渲染

程序部分使用C++语言，并且采用OpenCV库来简化图像的计算难度. 图8为工作流程图：计算机在获取得到摄像头原始画面以及灰度图片后，需要进一步识别和提取出线激光的光点像素坐标px或py值，代入测距公式求取实际距离.

图8 工作流程图

理论上，采集得到的参数px或py值是离散量，因此由式(3)求得的值也是离散的，所以最后根据式(1)或(4)求得的距离d会随着离散的x值或px值的变化而发生跳变，产生距离偏差. 因此，为提高计算得到的距离值的精度和分辨率，程序求取连续的px或py值，将激光光斑的亮度认为是二维高斯函数经过1次采样得到的.

进行程序设计时，采用质心法[15]，分别按照每帧图像的像素各行提取出线激光的各行光斑中心点，求取各光斑中心点的px或py值. 再将求得的px或py值，代入三角测距公式，求得空间各点的实际距离，得到相应的点云数据. 最后，将点云数据导入MeshLab，绘制出三维点云图(图9).

图9 三维点云图

3 实验系统扫描测试

3.1 三角测距参量拟合

利用三角测距原理对空间各点的实际距离进行计算时，需要用到多个参量值，在这里仅以求取式(4)中所需参量为例：激光器与基准线的夹角β，激光器中心点与摄像头中心点的距离s，摄像头焦距f，摄像头成像平面上单个像素感光单元的横向尺寸X和待测目标的反射光在摄像头成像平面上所成的像到一侧边缘的距离偏差值Δx. 其中，部分参量已设置为固定值，即夹角β=83°，距离s=100 mm，焦距f=4 mm.

单个像素感光单元的横向尺寸X和偏差量ΔX很难通过实际的测量求得，并且难以在安装时就控制好其数值的精度，其极小的偏差就会对测距的精度产生很大的影响. 因此，在装置制作完成后，再对这2个参量通过拟合进行确定.

在程序提取得到成像平面上线激光中间高度位置的px数值后，再通过人工测量出相应的实际距离，使用Matlab进行曲线拟合，确定出具体参量值. 其中，在求取测距参量时，采用先求取式(4)中距离d的倒数1/d，得到1/d与px数值的线性关系：

(14)

表1是参量拟合过程中采集得到的数据，图10为使用Matlab拟合得到的曲线图.拟合得到的曲线公式为

d-1=7.764×10-5px-0.021 0,

(15)

其中，R2=0.9995.

可以发现，采集得到的数据与拟合曲线的吻合程度较高，拟合效果较好.

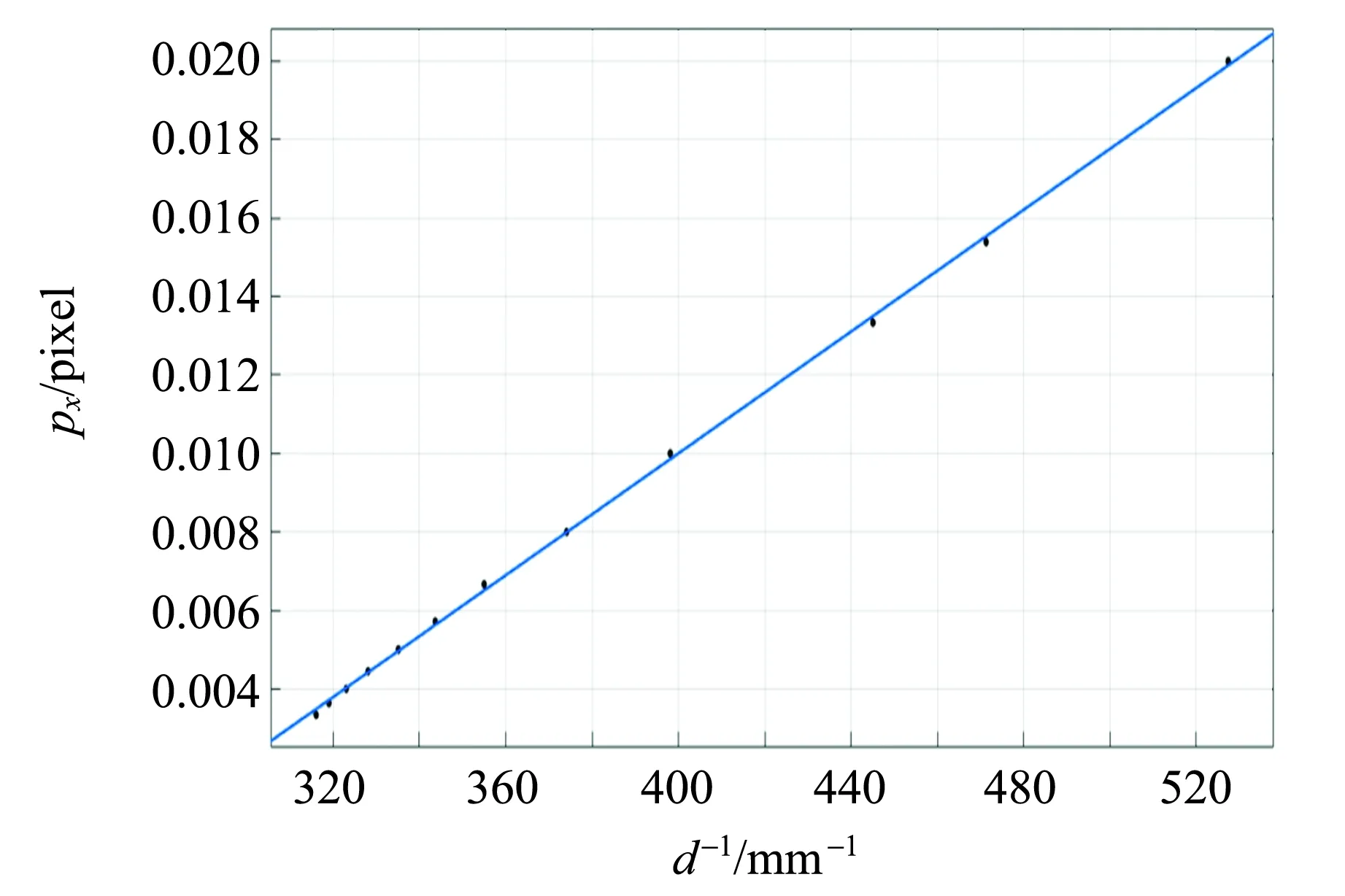
图10 测距参量拟合图像

与式(13)对比，即可得到相应参量值X=0.031 289 229 9 mm，Δx=-8.483 234 03 mm.

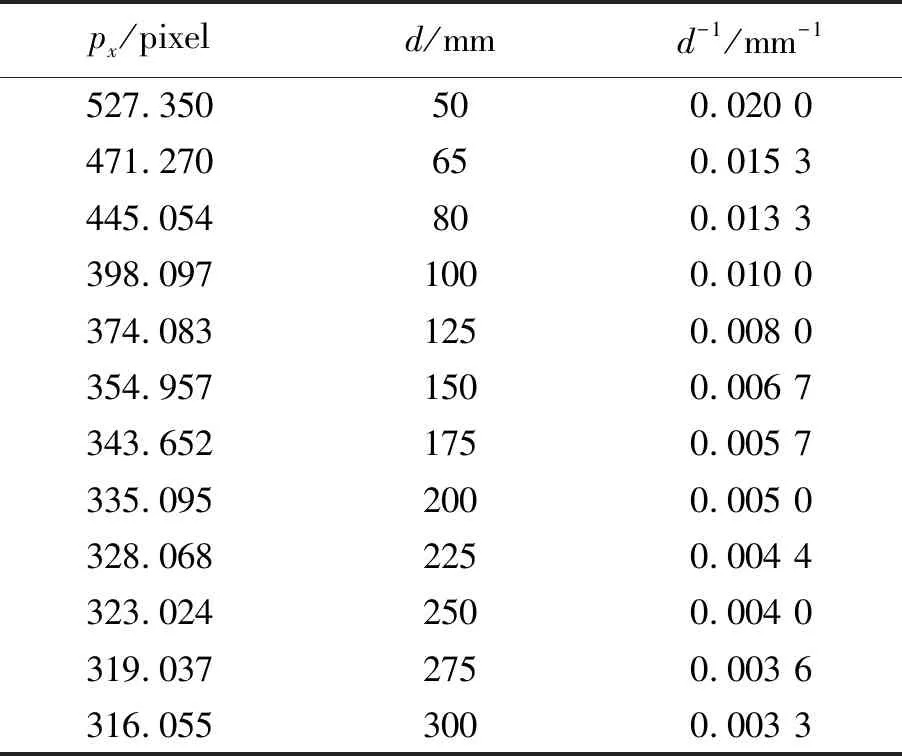
表1 拟合采集数据

3.2 性能测试

实验系统扫描角度范围为0°～180°，最小步进度数为1°，最远测量距离可达6 m.

为了检验系统的扫描效果，使用该系统180°扫描空间环境，得到三维点云图像与真实环境的对比图，如图11所示. 可以看出，该实验系统扫描效果较好，能够较清晰地绘制出待测空间环境.

图11 三维重建对比图

此外，为了检验系统扫描的精确度，将拟合得到的参数X和ΔX代入式(4)，对多个不同距离的线激光高度中心点位置到基准线的垂直距离d进行计算，并与实际距离值进行比较，得到数据见表2.

根据表2数据，绘制得到距离偏差值随px值的变化曲线如图12所示.

可以看出，实验系统的测距误差相对较小，最远6 m内误差在为90 mm以下，近距离1 m内误 差为5 mm左右. 此外，在测距距离较近时，实际值与计算值的偏差较小，但当距离逐渐变远时，二者的差值也逐渐增大. 这是由于根据式(1)或式(4)求得的距离d会随着离散的x值或px值的变化而发生跃变. 将式(1)改写为

(16)

并将x对d求偏导，得到

(17)

等式左右两边同时分子分母倒换，得到

(18)

由式(18)可以发现，随着测量距离d变远，d值随着离散的x值的变化而发生跃变的程度以d2的速度大幅增加. 所以，距离误差随着距离d的增加而不断增大.

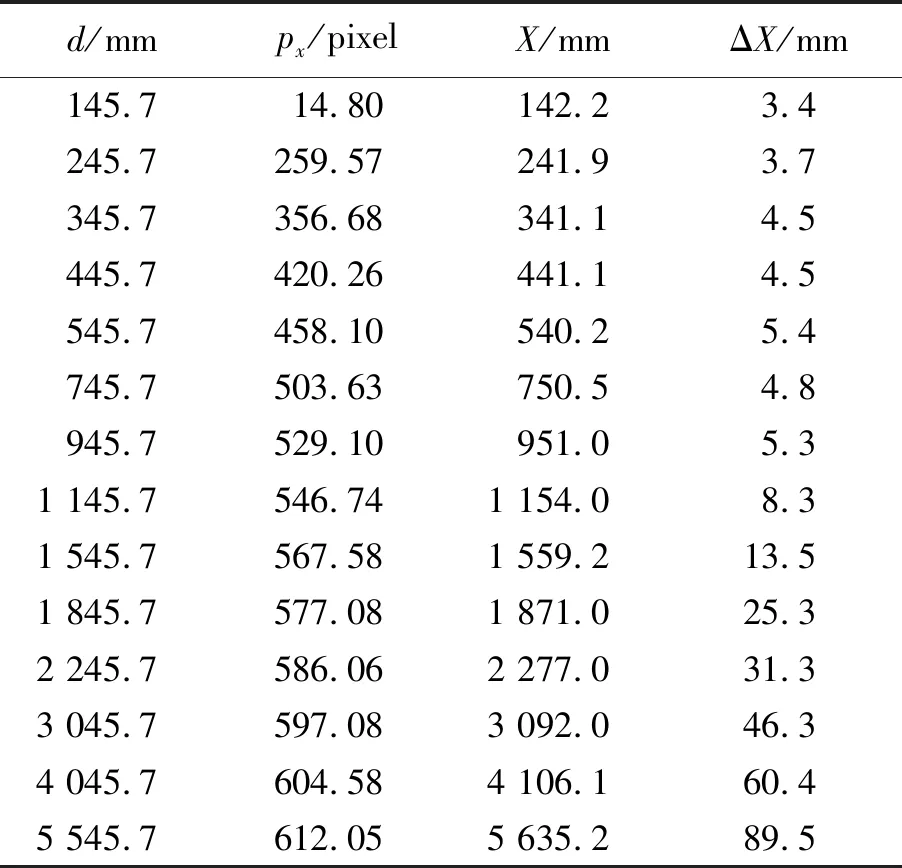
表2 距离值误差分析

图12 距离偏差值随值的变化曲线

4 结束语

通过使用拓展得到的空间三角测距原理，对待测空间环境进行三维重建，使用红外线状激光180°扫描待测空间，较精确地得到待测空间的三维图像. 该系统结构设计简单，操作简易且易于携带，成本也大幅降低.