基于Flac3D的加锚节理面抗剪性能数值模拟分析

(华南理工大学土木与交通工程学院 广东 广州 510641)

引言

天然岩体中存在有大量的节理，裂隙等结构面，为了保证岩体足够的连续性和稳定性，研究结构面的力学作用机理一直是学者们关心的问题[1]。刘泉声等通过室内物理实验，讨论了锚杆直径，法向应力等因素对于加锚节理面抗剪强度的影响规律[2]；Kim等综合分析认为，加锚试件力学性质与锚杆材料性质有关，但随着锚杆材料刚度增加，最终影响加锚试件力学强度的主要原因是岩石试件自身的力学性质[3]；李海波等[4]使用锯齿状混凝土岩石样品，研究不同剪切速率下的各种岩石节理起伏角度的强度特性。此外，一些学者用数值模拟软件来分析结构面的强度和变形特性，进行研究刘清朴等[5]使用3DEC程序，模拟单轴压缩试验并提出了相应的红砂岩关节模型；秦昊等[6]基于FEM程序探究一种能够计算出断续节理岩体加锚加固效应的数值分析方法。

综上所述，对于结构面特性的研究主要基于理论和室内试验方面，但是关于加锚节理面的作用机理和探究依旧较少，近些年随着计算机技术的成熟发展，采用高仿数值计算的方法来研究岩土工程问题已然成为了一种趋势和新的道路。其中，FLAC3D适合大多数岩石问题，本文拟采用FLAC3D来分析加锚节理的力学特性。

一、节理面锚杆剪切模型的建立

(一)锚杆受力及变形分析

锚杆的加固作用能够有效的限制节理面的剪切变形，剪切过程中，在剪胀作用下导致锚杆产生轴向力和轴向位移，以及切向力和切向位移，使得节理面处的锚杆呈“S”形变形，见示意图1(a)，1(b),结构面的剪切位移为Uo，法向位移为Ud。根据图1(a)，1(b)，由几何关系可以得到：

uo=0.5(Uocosα+Udsinα)

(1)

vo=0.5(Uosinα+Udcosα)

(2)

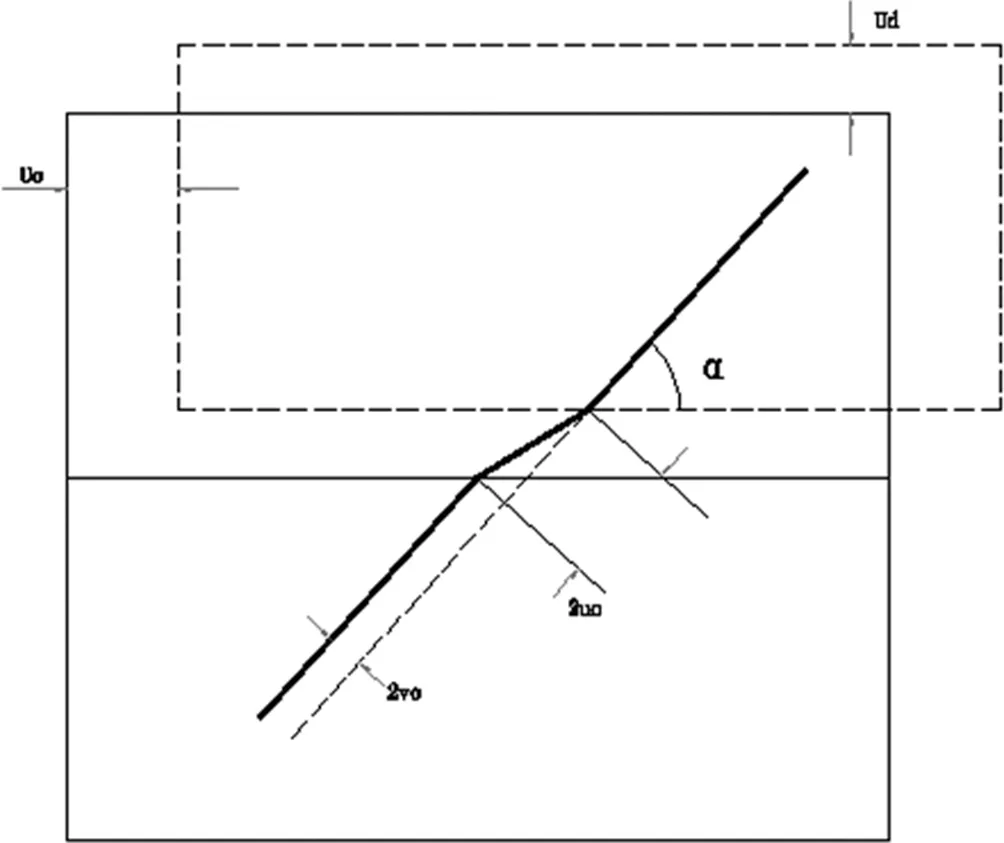
图1(a)结构面变形示意图

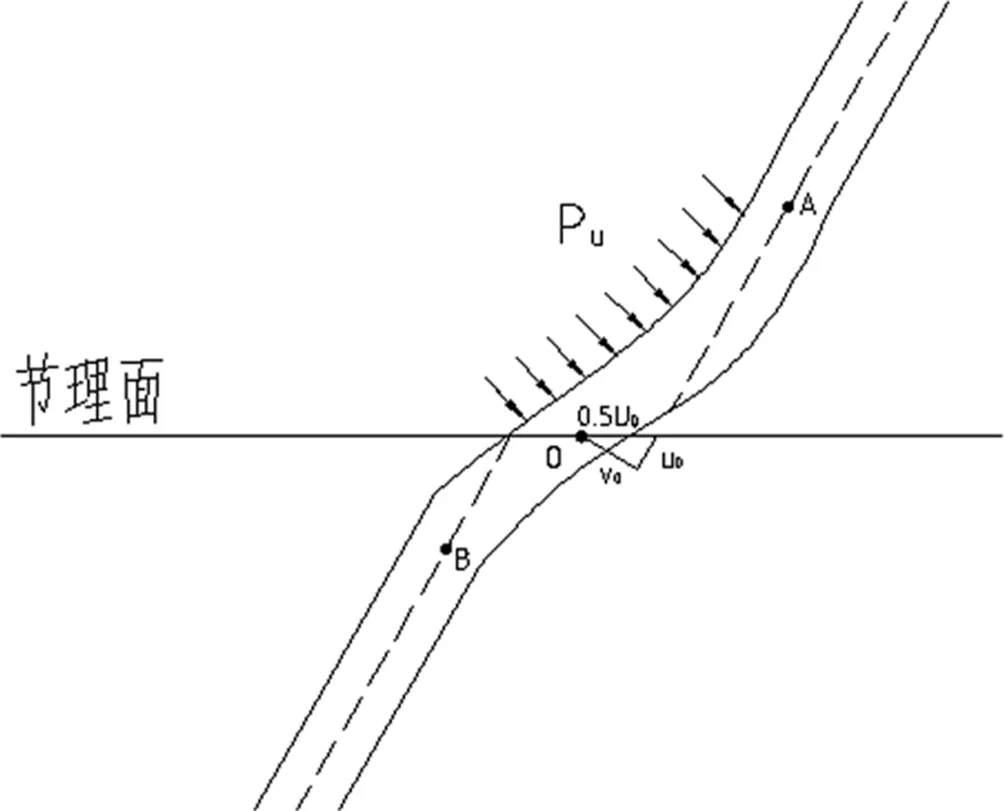
图1(b)锚杆变形示意图

他们之间的关系为Ud=Uotanψ[7]，ψ为结构面剪胀角。

节理面在剪切过程中，会发生剪胀效应，用剪胀角ψ来表示其剪胀效应的大小。Barton等[8]提出对数形式的峰值剪胀模型为：

(3)

式中：JRC为节理粗糙度系数，其取值可由Z.Y.Yang等[9]提出的方程确定。JCS为节理面壁的抗压强度。

Hetenyi[10]指出，在剪切过程中，位于节理一侧的锚杆截面横纵向位移满足：

(4)

(5)

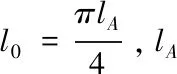
Pellet[11]根据势能驻值原理，考虑锚杆杆体初始位移分量uo和vo，得到了当余能最小时的真实位移场：

(6)

(7)

式中No，Qo分别为锚杆轴力和横向剪力，Pu为锚杆单位长度极限反力，E为锚杆的弹性模量，Db为锚杆直径，b为一常数，取0.27。

Holmberg[12]指出Pu主要与到围岩抗压强度σc和锚杆直径Db有关：

Pu=nσcDb

(8)

式中n一般在1～15之间取值，见图2：

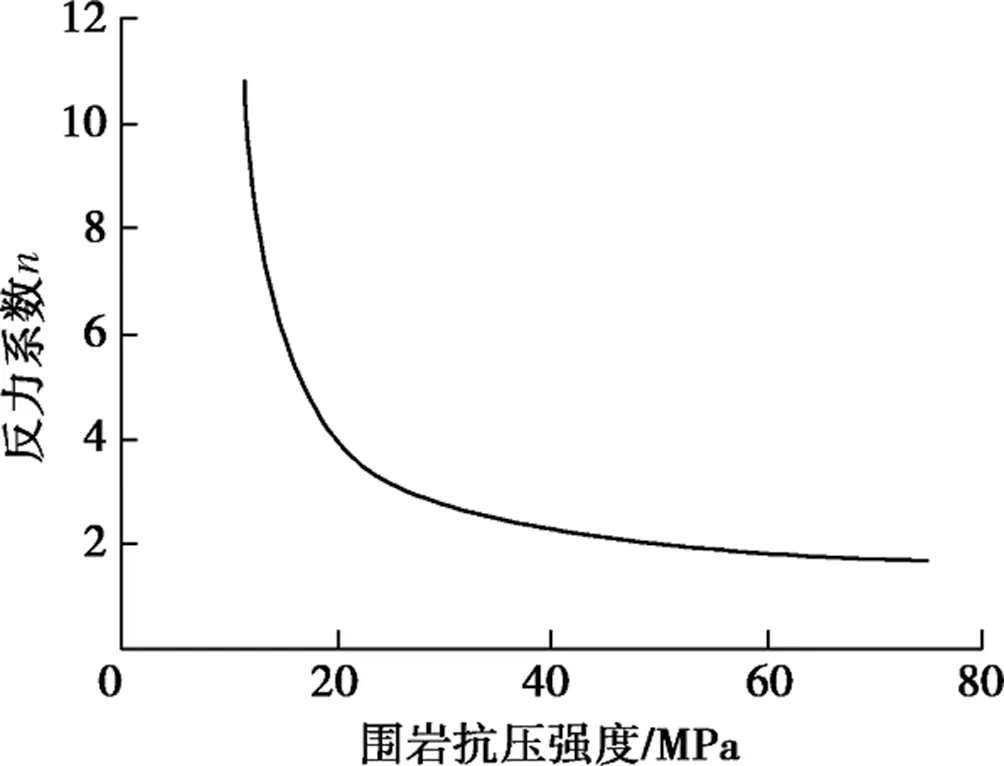
图2 n取值范围

张伟[13]分析认为节理岩体锚杆主要有两种屈服形式：拉剪屈服和弯曲屈服，两种屈服分别满足下式：

(9)

(10)

通过以上分析可知，在JCS，JRC及法向应力σn已知的情况下，可以计算得到节理面的剪胀角，继而在初始剪切位移Uo下，由Ud=Uotanφ可得节理面法向位移Ud，继而代入(1)，(2)式得到锚杆横纵向位移，由锚杆横纵向位移即可得到其轴力和剪力，将轴力和剪力代入(9)，(10)式是否满足，若满足，则可进一步判断屈服类型，不满足则继续迭代计算，直至满足为止。

(二)加锚节理面抗剪强度模型

加锚结构面的抗剪强度一般认为来自两方面的贡献[7]一个是节理岩体本身的抗剪强度τa，另一个是锚杆提供的抗剪力τb，则节理面加锚后的抗剪强度τ表达式为：

τ=τj+τb

式中：来自岩体本身的抗剪强度为τj=c+σjtan(φ+ψ)；

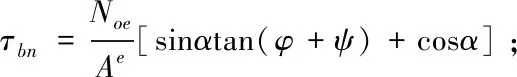
其中α为锚杆锚固角度，Ae为锚杆等效剪切面积[2]，Ae=DbL，Db为锚杆直径，L为试件边长或锚杆直径，其示意图见图(3)。

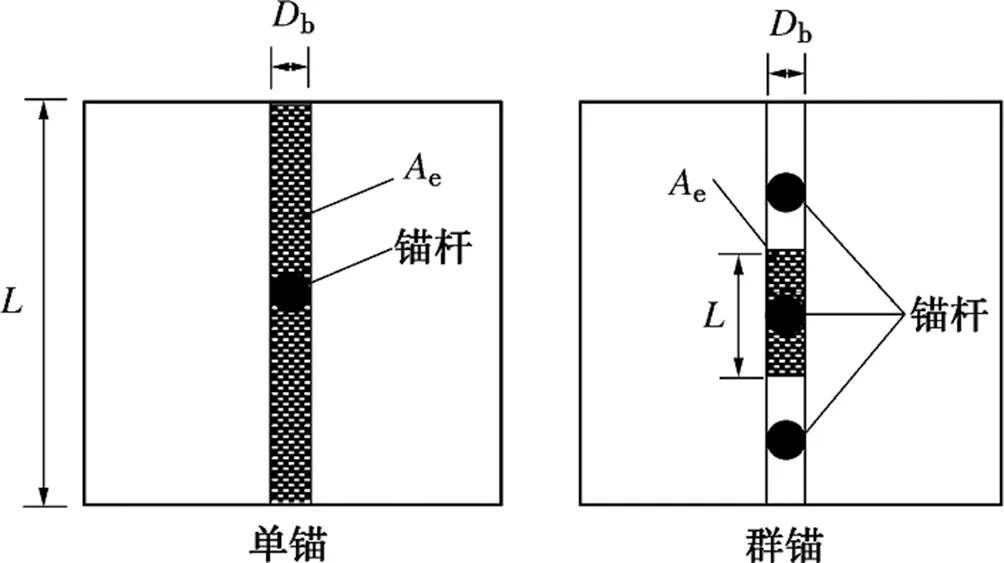
图3 锚杆等效剪切面积示意图

二、节理力学特性模拟

为验证上述节理抗剪强度模型的正确性，本文基于Flac3d模拟了加锚节理的直剪试验，并分析了加锚节理面的抗剪性能。

(一)计算模型

本文利用Flac3D进行建模和计算(见图4)，结构面试样模型尺寸为200mm×200mm×200mm，将结构面视为软弱结构面，其厚度为2mm。

计算采用Mohr-Coulomb准则，岩体参数：弹性模量20Gpa，泊松比0.2，黏结力0.75Mpa，密度2500kg/m3，内摩擦角37°；结构面参数：节理面剪切刚度8Gpa/m，节理面法向刚度90Gpa/m，节理内摩擦角30°，节理粘聚力0.06Mpa；锚杆参数：弹性模量200Gpa，屈服强度500Mpa，砂浆及岩体接触面剪切刚度0.5Gpa/m，锚杆长度120mm。

模型的边界条件：模型上部为自由边界，底部固定约束，垂直方向上上表面施加法向应力，下表面限制垂直位移。数值试验过程中，上部岩体施加位移荷载，8位移大小为1×10-3mm/计算时步，使其发生移动。

图4 三维模型

(二)应力应变曲线特征

在直剪试验数值模拟过程中,加锚和未加锚的情况下,结构平面的应力-应变状态表明两者具有接近直线的弹性应变状态，对于没有锚杆加固的结构面：曲线在剪切应力达到峰值后表现出明显的应变软化特性，随着剪切位移的增加，而剪切应力基本保持不变;对于具有锚固状态的结构面，在弹性阶段之后，它表现出明显的应变强化特性：随着剪切位移的增加，剪切应力逐渐增大，然后保持不变，表明在结构表面达到峰值剪切强度后，主要是锚杆提供剪力强度进行抗剪，直到锚杆达到屈服状态。

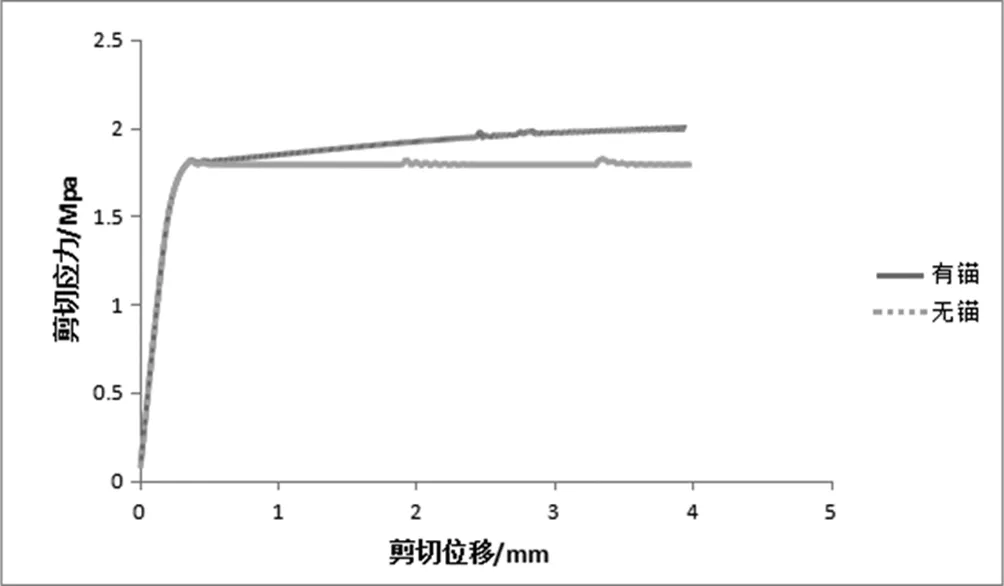
图5 有锚与无锚状态的应力应变关系对比

(三)剪切强度特征

为了比较结构面锚固条件下抗剪强度的变化，在不同法向应力下记录试样的剪切强度值：

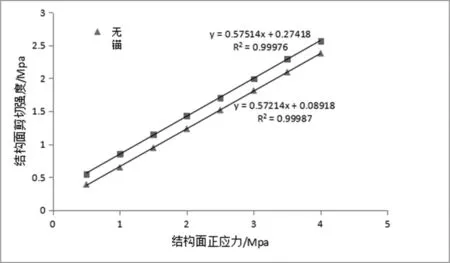
图6 有锚和无锚状态结构面的剪切强度对比

可以看出，锚固后结构面的抗剪强度明显提高，剪切强度τ和结构面法向应力σn之间呈线性关系，Mohr-Coulomb准则用于拟合方程(示于图中)，即：

τs=c+σntanφ

通过曲线拟合的方式发现，结构面加锚后主要增加结构面的等效黏结力，而等效内摩擦角与加锚前相比没有明显变化，说明锚杆主要发挥了其轴向作用的抗剪能力。

根据图2，取反力系数n=3.由前面所述的计算流程，计算得到结构面的剪切强度。通过对比两者的计算结果发现(如图所示)：两者的数据基本一致，说明上面建立的加锚节理面抗剪强度模型较为合理。

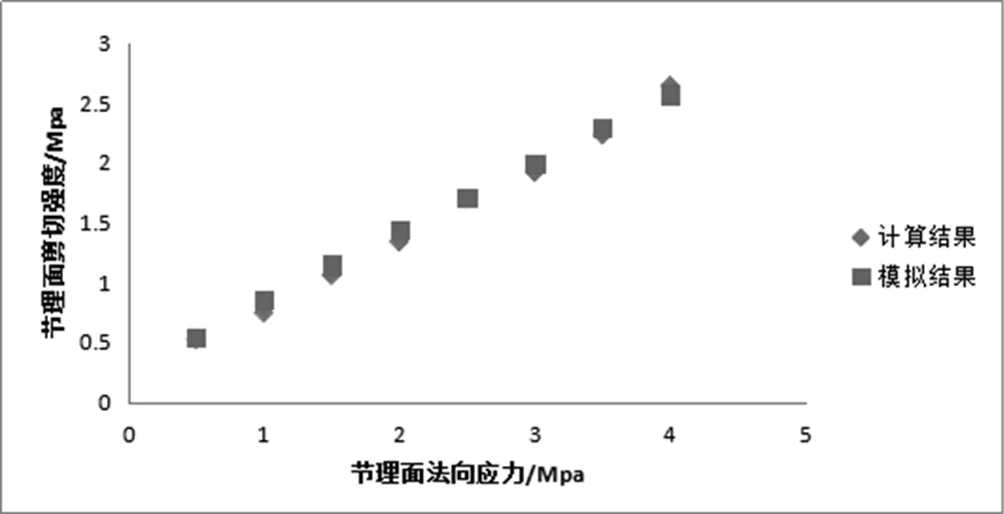
图7 数值计算与理论计算的加锚节理面剪切强度对比

三、结论

(1)在考虑了节理面剪胀角及“等效剪切面积”后建立的剪切强度模型，数值模拟结果与理论计算结果有较高的契合性。

(2)加锚后的结构面其剪切强度有明显的增加，通过数值模拟分析发现，其剪切强度的提高主要等效提高了结构面的黏结力，摩擦角基本不变。【参考文献】

[1]白世伟，任伟中，丰定详等.共面闭合断续节理岩体强度特性直剪试验研究[J].岩土力学，1999,20(2)：10-16.

[2]刘泉声，雷广峰；节理岩体中锚杆剪切力学模型研究及试验验证[J].岩土工程学报，2018，05(05)：794-801

[3]KIM H J,HU J W,HWANG W S.Cyclic testing for structural detail improvement of CFT column-foundation connections[J].Sustainability,2015,7(5):5260-5281.

[4]李海波，冯海鹏，刘博.不同剪切速率下岩石节理的强度特性研究[J].岩石力学与工程学报，2006,25(12)：2435-2440.

[5]刘清朴等，3DEC中红砂岩节理模型开发及数值模拟[J].中国农村水利水电，2017,4:137-142.

[6]秦昊，断续节理岩体锚固效应数值模拟方法研究[D].济南：山东大学，2010

[7]张伟,刘泉声.节理岩体锚杆的综合变形分析[J].岩土力学,2012,33(4):1067-1074.ZHANG Wei,LIU Quan-sheng.Synthetical deformation analysis of anchor bolt in jointed rock mass[J].Rock and Soil Mechanics,2012,33(4):1067-1074.

[8]BARTON N,CHOUBEY V.Thhe shear strength of rock joints in theory and practice[J].Rock Mechanics,1977,10(1/2):1-54.

[9]YANG Z Y,LO S C,DI C C.Reassessing the joint roughness coefficient(JRC)estimation using Z2[J].Rock Mechanics,2001,24(3):243-251.

[10]HETENYI M.Beam on elastic foundation:Theory with applications in the fields of civil and mechanical engineering[M].Ann Arbor:The University of Michigan Press,2013.

[11]PELLET F,EGGER P.Analytical model for the mechanical behavior of bolted rock joints subjected to shearing[J].Rock Mechanics and Rock Engineering,1996,29(2):73-97.

[12]HOLMBERG M.The mechanical behavior of untensioned grouted rock bolts[D].Stockholm:Royal Institute of Technology,1991.

[13]葛修润,刘建武.加锚节理面抗剪性能研究[J].岩土工程学报,1988,10(1):8-19.