含三聚氰胺多孔材料分层复合介质吸声特性∗
2019-04-02白聪沈敏
白 聪 沈 敏
(武汉纺织大学 数字化纺织装备湖北省重点实验室 武汉 430073)
0 引言
近年来,科研工作者对多孔材料吸声特性进行了大量的研究,多孔材料一般可以充当吸声结构的填充层,实际工程中大都采用多孔材料与其他高分子薄膜、弹性板或者空腔复合,形成分层复合结构,使得声波在复合结构中逐层衰减,可以达到较好的吸声效果,在建筑、航空、交通工具等工程领域有广泛的应用[1]。相比传统的聚氨酯材料,三聚氰胺泡沫属于高开孔率多孔材料,有着优良的吸音、隔热、防火和环保特性,可作为新一代的声学材料。研究者开始使用三聚氰胺泡沫与其他弹性板、空腔复合形成复合结构,例如:三聚氰胺泡沫可以和毛毡、纤维、金属箔和塑料薄膜等模压在一起制成轮廓填充部件,作为隔音器、消音器、隔热板等结构的吸声或隔声材料[2−3],也可作为层压式吸音单元,安装在汽车引擎罩的下方用于空腔填充,或者铺设在车身端壁前以及传输通道内,用于发动机机舱消音。
已经有许多学者对含多孔材料复合结构的隔声特性做了研究。Bolton等[4]首次采用Biot理论[5−6]较完整地建立了复合板结构隔声特性理论模型,以聚氨酯芯层双层复合板作为算例,分析含多孔材料-空气-弹性板复合结构的隔声特性,并通过实验验证了该理论计算结果具有较高的精度。在此基础上,Liu[7]同样对三层聚氨酯芯层复合板结构隔声量进行了研究,计算了六种不同布局的复合结构隔声量。詹沛等[8]采用传递矩阵法推导了隔声量计算公式,给出了空气层与多孔材料对复合结构的隔声特性影响。
在实际使用中,多孔材料经常和空气层、薄膜结合形成非均匀复合结构,可以在较宽频率范围内获得令人满意的吸声效果。目前,对于此类复合结构的吸声特性,国内外学者也展开了理论与实验研究,主要有声电类比法[9]、传递矩阵法[10−11]、解析法[12−13]、阻抗管实验法[14−15]。Pieren等[9]使用声电类比法推导了多层纤维材料和空腔复合结构的垂直入射吸声系数计算公式,以双层纤维多孔材料加空腔复合结构为例,计算了垂直入射吸声系数,通过阻抗管实验验证了理论模型结果的正确性,并且优化了纤维材料的流阻、质量、厚度等参数。但是,采用声电类比法时,如果对含有的空腔进行等效电路分析时,电路结构复杂,容易出错,尤其是对于穿孔板还需要做修正。
Wang等[10]将多孔材料和弹性板组合形成双层复合板结构,基于Biot理论结合传递矩阵方法推导了声波垂直入射的吸声系数,详细分析了多孔材料流阻、厚度、压缩率参数对吸声特性的影响。Liu等[11]使用微穿孔板、多孔材料、空腔组合成复合结构,先根据马大猷提出的理论模型计算微穿孔板声阻抗,和Johnson-Champoux-Allard(JCA)提出的等效流体模型计算多孔材料声阻抗,并结合传递矩阵数学方法推导了多层复合结构的吸声系数,最后通过阻抗管实验对理论结果进行了验证。文中详细探讨了空气层厚度和微穿孔板的穿孔率对复合结构吸声特性的影响。刘新金等[12]、宁景锋等[13]采用Johnson-Allard(JA)模型和波动学理论,建立声波在分层介质中传播方程,推导了多孔材料背衬刚性壁面和多孔材料背衬空气介质的双层复合结构的垂直入射吸声系数,详细分析了多孔材料孔隙率、流阻率和空气背衬层厚度等参数对双层结构吸声特性的影响。但是,JA等效流体模型不考虑多孔材料骨架和空气流体的耦合作用,对于其中的一些参数需要做修正。
赵松龄[14]通过实验研究,对比了采用玻璃纤维布和塑料薄膜分别作为护面层时,泡沫塑料块垂直入射吸声系数,指出薄膜护面层适合中低频范围。但是文中并没有给出泡沫塑料多孔材料的具体声学参数,后来学者很难进行理论计算、定性分析多孔材料加了薄膜护面层后的吸声特性。姜生等[15]将穿孔板与氯化聚乙烯(CPE)/七孔涤纶短纤(SHPF)薄膜材料复合形成多层孔膜结构,同样采用驻波管实验测试了多层孔膜复合结构的吸声系数,详细分析了穿孔板与CPE/SHPF薄膜采取不同组合方式的吸声特性。如果仅采用实验研究法,费时费力,成本高,测量结果受实验条件影响较大。
综上所述,已有的研究局限于分析垂直入射吸声特性,不考虑声波从其他角度入射的效果,而无规入射吸声系数是声波从各个角度入射时的平均值,更加符合工程实际应用。以往的理论和数值分析大多采用JCA或者JA等效流体模型来对多孔材料进行建模,不考虑空气-骨架耦合作用,是一种简化的模型,结果不够精确。特别是针对含薄膜护面层复合结构的吸声特性研究,大多采用实验方法,既费时又费力,成本高,结果容易受到测试条件的影响。针对含薄膜、多孔材料和空气的非均匀复合结构,还缺乏完整的理论或者数值分析方法。
因此,本文基于Biot理论模型,充分考虑不同介质之间耦合边界条件,研究含多孔材料、薄膜和空腔等多种不同介质背衬刚性壁面结构的无规入射吸声特性,比已有的研究方法,可以更加准确地评估多孔材料有薄膜护面层、空腔的复合结构的吸声特性。首先,本文基于Biot理论模型计算声波在多孔介质中传播的波数,继而推导了多孔材料与空气或薄膜等不同种介质相互耦合时的边界条件,建立了非均匀复合材料背衬刚性壁面结构的无规入射吸声系数理论计算模型,并通过阻抗管实验验证了理论结果,以含三聚氰胺多孔材料、空气和薄膜的三种介质并且背衬刚性壁面结构为例,详细分析了改变多孔材料布局和主要参数对复合结构吸声特性的影响。
1 弹性多孔介质中的声传播
设有一束单位振幅的平面波以角度θ入射到无限大多孔弹性介质表面,如图1所示。仅考虑二维情况,入射波的速度势函数可表示为
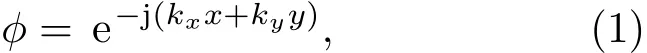
其中,k= ω/c,kx=ksinθ,ky=kcosθ,k、ω、c分别为声波的波数、角频率和声速。

图1 声波入射到多孔弹性介质Fig.1 Acoustic waves incident on porous elastic media
声波在均匀且各向同性的流体饱和多孔弹性介质中传播时,以快纵波、慢纵波和切变横波三种形式传播[4]。以k1、k2和kt分别表示为快纵波、慢纵波和切变横波的波数,可以表示为
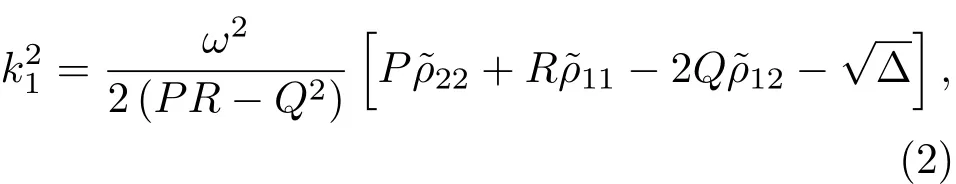
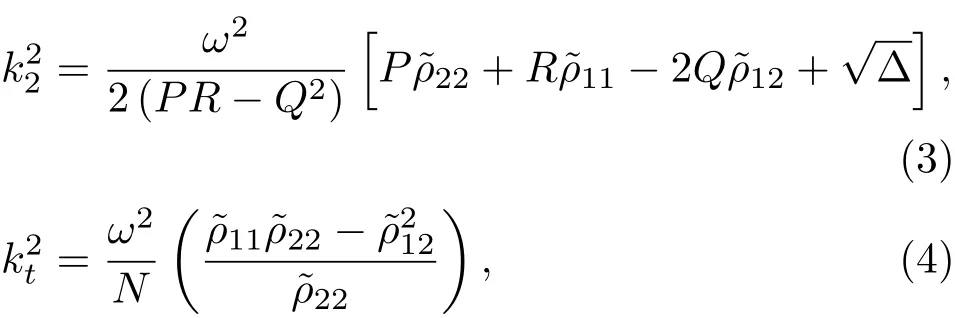
其中,弹性因数P、Q、R、N以及∆可以表示为
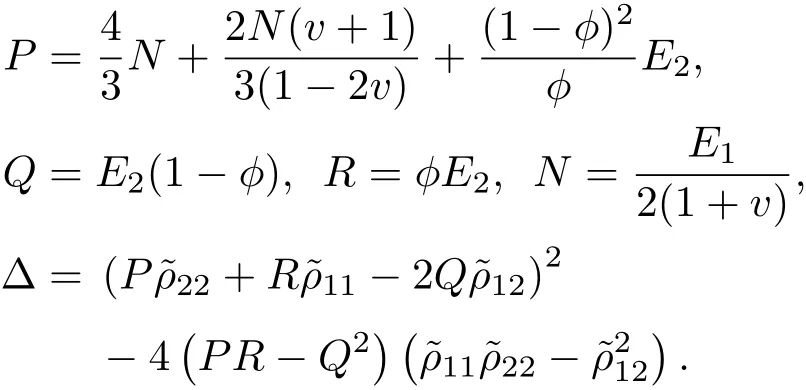
与质量有关的参数如下所示:
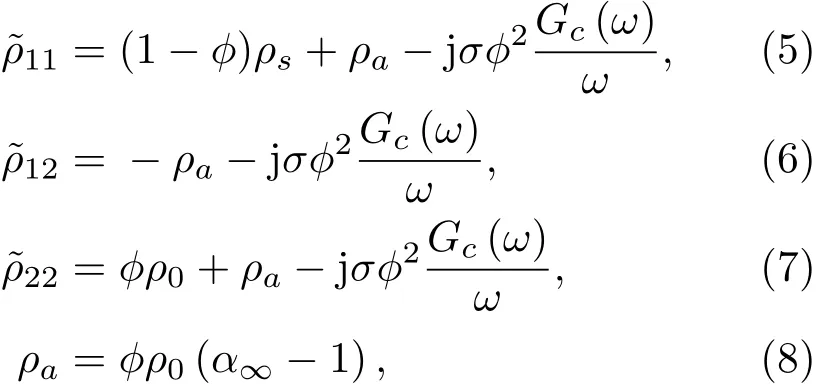
其中,ρ0为流体的密度,ρs为固体骨架的密度,ρa为两者的耦合密度,ϕ为介质孔隙率,ν为泊松比,α∞为多孔介质的几何结构因数。
假设介质中孔隙是圆柱体结构,则有
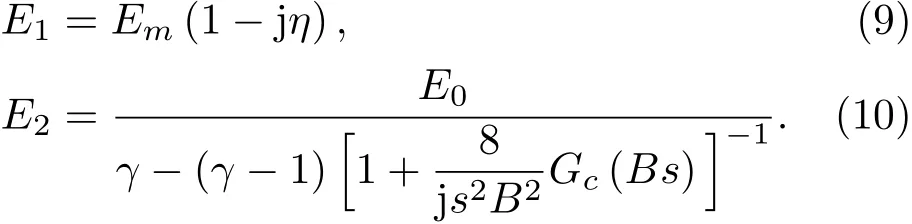
黏性相关频率函数如下:
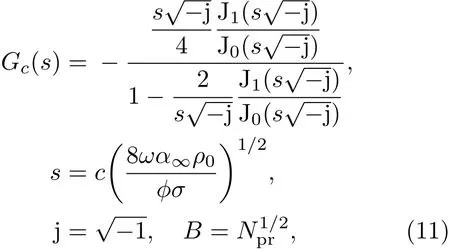
其中,E1为真空中固相的杨氏模量,E2为孔隙流体的体积弹性模量,Em为固体静态杨氏模量,η为损失因数,γ为比热比,c为孔的形状因子,Npr为普朗特数,σ为流体的静态流阻,j为虚数单位,J0,J1别为零阶和一阶第一类Bessel函数。
而k1y、k2y、kty分别为快纵波、慢纵波和切变横波波数在y方向上的分量,如下所示:
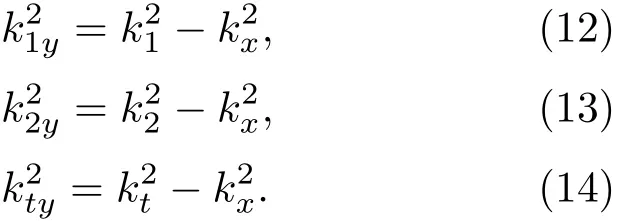
根据Bolton等[4]的分析可得到介质中固体骨架和流体分别在x方向和y方向上的位移:

介质中固体骨架在y方向的应力分量σy、流体的应力s和xOy平面上的剪切应力τxy表示如下:
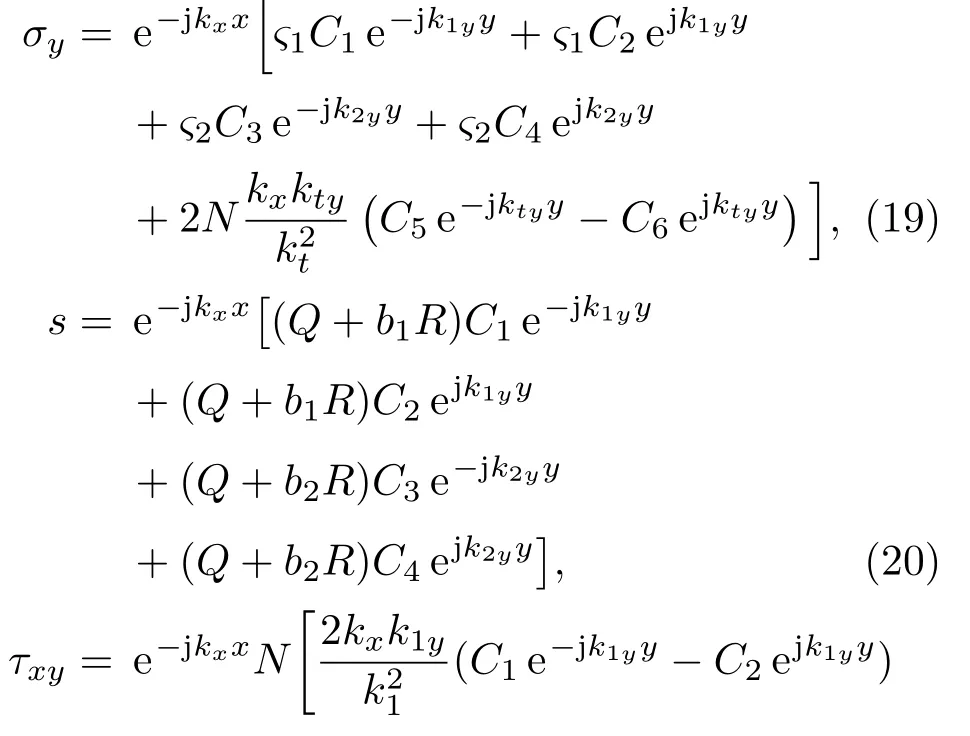
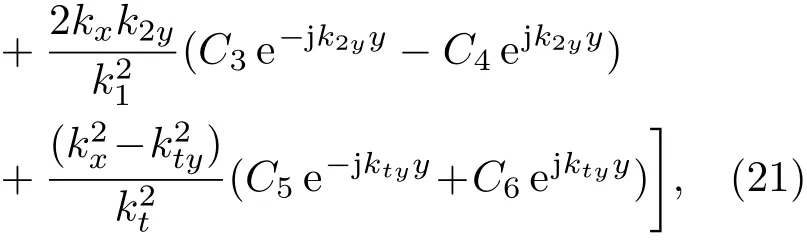
其中,

式(15)∼式(21)中的参数C1∼C6由多孔材料和其他介质耦合时的边界条件决定,可分为多孔材料直接固定于弹性板或者通过空气与板耦合。
2 复合材料背衬刚性壁面边界条件
2.1 不同耦合条件
图2为含多孔材料分层复合结构背衬刚性壁面结构,假设分层介质相对面积很大,可不考虑边界效应,平面波Pi斜入射到第一层介质前面,中间多层介质相互耦合,最后一层介质背衬刚性壁面。当分层介质背衬刚性壁面时,认为平面波只有反射分量Pr,而没有透射分量Pt,在刚性壁面分界处的边界条件和计算隔声量时不同。
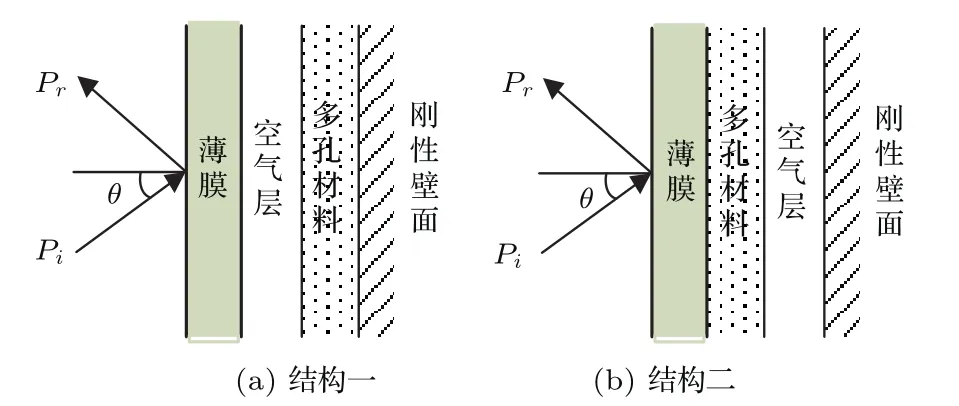
图2 声波无规入射,含多孔材料复合结构背衬刚性壁面Fig.2 Porous material composite structure backing rigid wall surface when acoustic random incidence
Bolton等[4]已经针对多层复合板结构隔声特性进行了研究,对分层介质相互耦合的边界条件进行了较完整的推导,但是计算隔声特性时,弹性板两侧均为空气流体。本文分析多层复合材料背衬刚性壁面结构的吸声特性,需要推导刚性壁面处的边界条件。因此,本文增加一种多孔材料与刚性壁面绑定和空气层与刚性壁面耦合的边界条件。
如图3(a)所示,当结构最后一层介质为多孔材料,并且多孔材料右侧与刚性壁面绑定在一起,其分界面边界条件为uy=0,Uy=0,ux=0。如图3(b)所示,当最后一层为空气介质,并且右侧与刚性壁面绑定在一起,其分界面边界条件为vy=0。
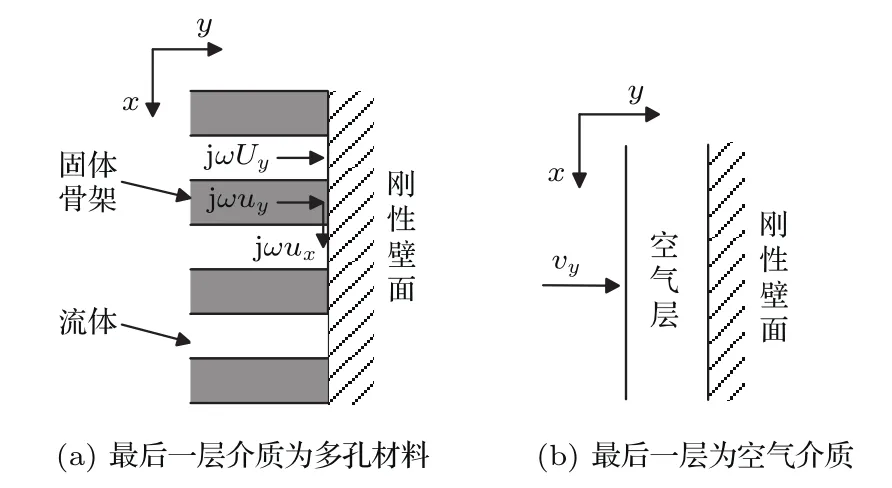
图3 多孔材料或空气层背衬刚性壁面Fig.3 Porous material or air backing rigid wall
图4 (a)为多孔材料左侧直接与薄膜绑定在一起进行耦合的示意图,若不考虑板的刚度,弹性板就变成了薄膜,此时板刚度D=0。设薄膜的横向位移为wt=Wt(x)ejωt,薄膜的中心面的位移为wp=Wp(x)ejωt,则多孔材料与薄膜的分界面处边界条件为vy=jωWt,uy=Wt,Uy=Wt,。其中,hp是薄膜的厚度,ms是板的面密度,qp=−σy−s是多孔材料介质作用在薄膜上的应力。
图4(b)为多孔材料通过空气层与薄膜进行耦合的示意图。薄膜-空气分界面边界条件为v1y=jωWt,v2y=jωWt,P1− P2=(Dk4x− ω2ms)Wt。其中,P1、P2为薄膜两边在空气中的声压,v1y、v2y为薄膜两边空气介质的质点速度。空气层-多孔材料分界面边界条件为−hP=s,−(1−h)P= σy,vy=jω(1−h)uy−jωhUy,τxy=0。其中,P 是界面处的外部声场的压力,vy是界面处外界介质的质点速度。

图4 不同耦合情况Fig.4 Dif f erent coupling conditions
将多孔介质中固体骨架和流体分别在x方向和y方向上的位移(公式(15)∼(18)),和固体骨架在y方向的应力分量σy(公式(19))、流体的应力s(公式(20))和xOy平面上的剪切应力τxy(公式(21))分别代入分层结构在每个分界面处的边界条件,就可以得到一组关于反射系数R的线性方程组,利用Matlab软件求解线性方程组就可以求出反射系数。附录A完整给出了声波斜入射时,计算BB结构反射系数的方程组,其他结构可以参考BB结构的算例,就可以列出多孔材料不同布局时计算反射系数的线性方程组。继而求出吸声系数α(θ)=1−|R|2,再对其进行积分即可求得无规入射时的平均吸声系数¯α:¯α=2∫θlim0α(θ)sin(θ)cos(θ)dθ。其中,θlim为入射声波的最大角度,通常建议在70◦∼85◦之间取值,本文中取值75◦。
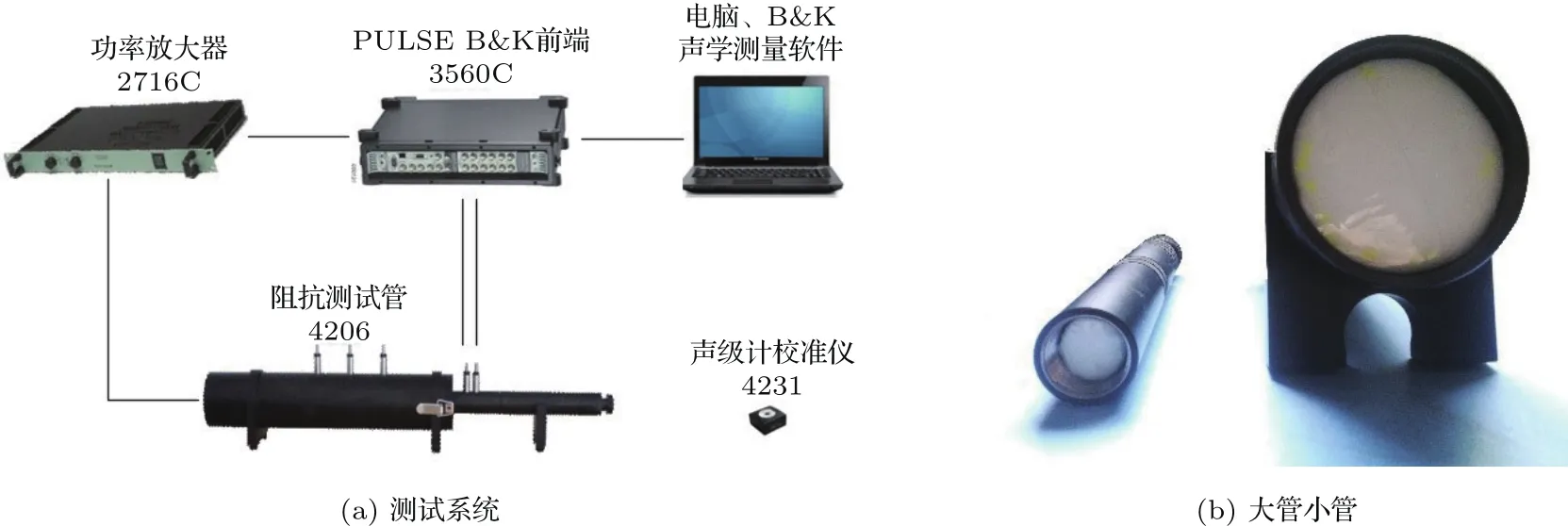
图5 阻抗管测试系统Fig.5 Impedance tube test system
2.2 阻抗管实验
本文采用阻抗管实验验证理论模型的可行性,由B&K公司测试系统、4206T型阻抗管、2716C型功率放大器、3560C型前端和声级计校准仪组成。阻抗管分为大管和小管,其中大管直径100 mm,传声器之间的距离为50 mm,测量频率范围为50 Hz∼1000 Hz;小管直径29 mm,传声器之间距离设置为20 mm,测量频率范围为500 Hz∼5 kHz,图5为阻抗管测试系统以及被测样品安装图。
3 三聚氰胺多孔材料复合结构吸声特性
3.1 实验验证单层结构与复合结构吸声系数
为了验证理论模型的有效性,同时建立单层多孔材料模型以及建立“薄膜+多孔材料+空气层+刚性壁面”复合结构模型,计算垂直入射下吸声系数,并采用阻抗管实验验证理论计算结果。多孔材料实验样品参数如表1所示,薄膜厚度为1 mm,面密度为ms=0.03 kg/m2,多孔材料厚度为25 mm,空气层厚度为5 mm。
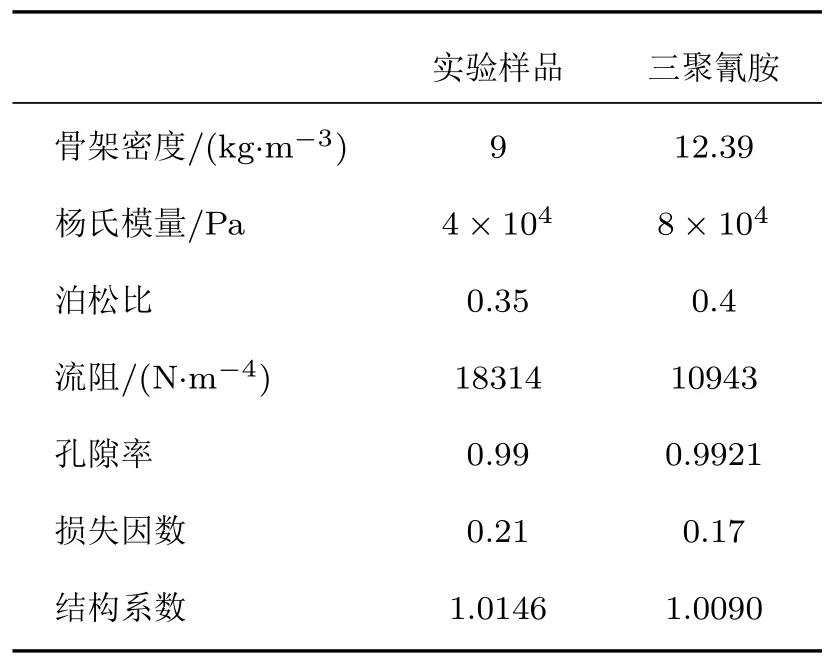
表1 三聚氰胺泡沫的参数Table 1 Melamine foam parameters
图6显示了单层多孔材料背衬刚性壁面结构,利用本文推导的理论模型和阻抗管实验得到的垂直入射吸声系数。从图6中可以看出,采用本文推导的理论模型计算得到的吸声系数与实验结果在2000 Hz频率附近都明显出现了一个波谷,在其他频率范围内得到的吸声系数基本与实验结果趋势一致。
图7对比了在“薄膜+多孔材料+空气层+刚性壁面”复合结构模型下,即后文中的BU结构,利用本文推导的理论模型和阻抗管实验测量的垂直入射吸声系数。从图7中可以看出,理论模型的结果和实验结果基本一致,但是中高频段实验测量结果略高于理论计算结果,但在总的频率范围内得到的吸声系数基本与实验仿真结果趋势一致,故该理论模型具有可行性。
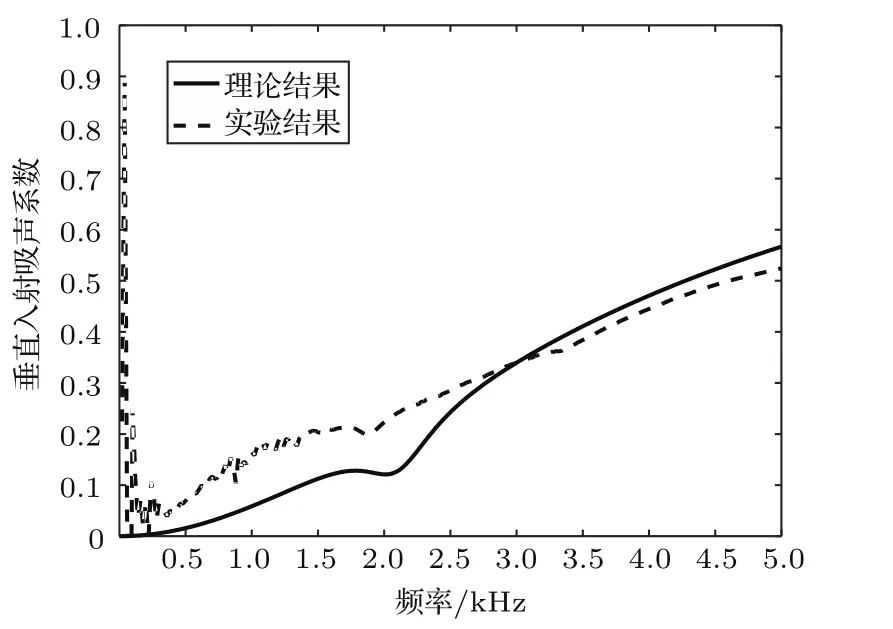
图6 单层结构的垂直入射吸声系数对比Fig.6 Comparison of normal incidence sound absorption coefficient of single layer structure
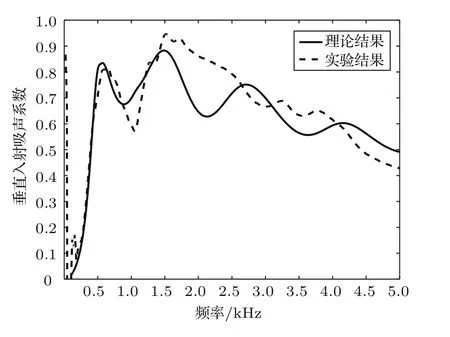
图7 BU结构的垂直入射吸声系数对比Fig.7 Comparison of the normal incidence sound absorption coefficient of BU structure
3.2 三聚氰胺泡沫在不同布局下的无规入射吸声特性
三聚氰胺泡沫材料具有高开孔率三维网络结构体系,开孔率高达99%以上,还具有超轻质及良好的二次加工性能及阻燃隔热性能,是一种综合性能良好的多孔吸声材料。三聚氰胺多孔材料选择Naoki等[16]提供的一种“Illtec”样品,参数如表1所示。主要讨论以下四种不同的结构布局UU、BU、UB和BB,如图8所示。其中,结构UU指的是三聚氰胺泡沫材料分别与薄膜、刚性壁面分离;结构BU是芯层一侧与薄膜绑定,另一侧与刚性壁面通过空气层耦合;结构UB是指多孔材料左侧与薄膜通过空气层耦合,右侧与刚性壁面结合;结构BB是指多孔材料左侧与薄膜、右侧与刚性壁面固定。

图8 多孔材料不同布局分层复合介质结构Fig.8 Porous materials with dif f erent layout layered composite media structure
本节主要分析平面波斜入射到复合板表面,三聚氰胺泡沫分别呈现不同布局时的吸声特性。四种结构中每层薄膜厚度均为L=1 mm,薄膜面密度为ms=0.005 kg/m2。三聚氰胺泡沫的厚度为lp=25 mm,结构BU、UB中空气层的厚度为la=2 mm,结构UU中空气层的厚度为la1=la2=1 mm,三聚氰胺参数参考表1。

图9 不同布局对分层复合结构吸声系数影响Fig.9 Ef f ect of dif f erent layout on sound absorption coefficient of layered composite structure
图9 对比了BB、BU、UB、UU结构吸声系数,可以发现UB和UU两种结构的吸声特性曲线基本吻合,UB结构在500 Hz以下的吸声系数会高于UU结构,在1000 Hz∼2300 Hz的吸声系数低于UU结构。在高频段,UB和UU两种结构的吸声系数曲线都比较平滑,趋于恒定值0.8左右。对比这四种结构的吸声系数曲线,可以发现当声波入射到复合结构时,如果在多孔材料前面添加空气层可以改善复合结构在高频部分的吸声特性,但在低频部分会有所损失。从全频段上综合来看,UU结构可以获得较宽的吸声频率范围。比较图9中BB、BU结构的吸声系数,可以发现在多孔材料后面增加一层空气介质时,BB结构的吸声系数曲线的波峰会向低频段移动。采用BU结构,可以改善1000 Hz以下低频范围的吸声系数。在整个频率范围内,BB和BU结构的吸声系数最大值达到0.9,获得了一个较好的吸声特性。
3.3 薄膜不同面密度对吸声系数的影响
选择多孔材料两侧分别与薄膜固定,即BB这种结构布局,保持其他的参数不变,仅改变薄膜的面密度,计算声波斜入射到BB结构表面时的吸声系数。结构中的薄膜面密度分别取四个值进行讨论:(1)ms=0.005 kg/m2,(2)ms=0.05 kg/m2,(3)ms=0.15 kg/m2,(4)ms=0.25 kg/m2。
图10显示了在BB布局下,薄膜取不同面密度时对双层板结构的吸声系数的影响。从图10中可以看出,随着薄膜面密度的增加,吸声曲线第一个波峰会向低频移动,但其所达到的吸声系数最大值都为0.9左右,可以改善低频段的吸声系数,而第一个波谷的吸声系数就会明显下降。在高频部分,吸声系数会随着面密度的增加而下降。所以降低薄膜的面密度,虽然会导致低频端吸声系数减小,但在其他频段会有一个非常大的提升。
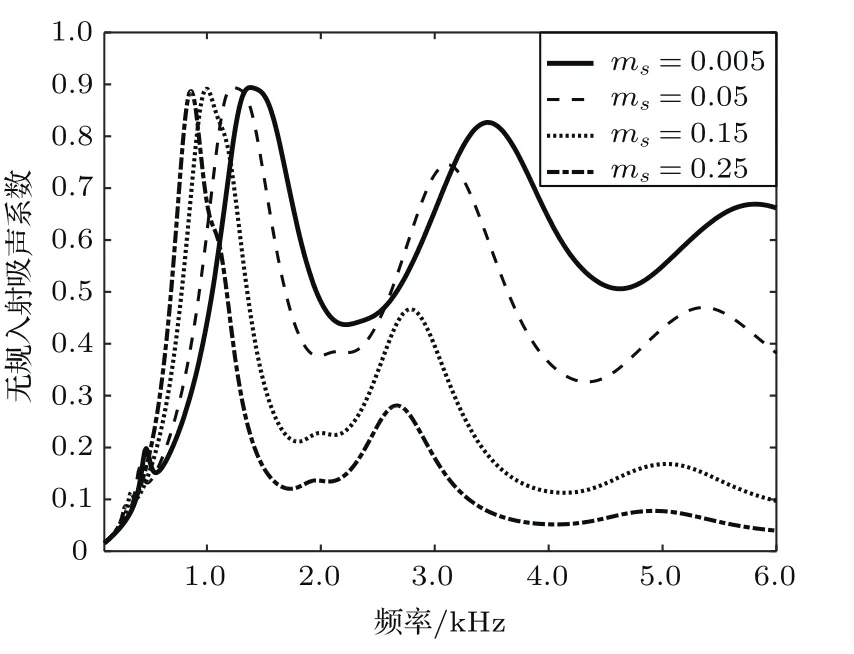
图10 薄膜面密度对无规入射吸声系数影响Fig.10 Ef f ect of f i lm surface density on random incident sound absorption coefficient
4 结论
(1)对比BB、BU、UB结构的吸声系数发现,在分层复合结构中增加空气层对吸声系数有一定的改善。在多孔材料后面增加一层空气层,可以有效改善双层复合板结构在低频段的吸声系数;在多孔材料前面增加一层空气层,损失一部分低频段的吸声系数,但高频段的吸声系数有较大的提升。
(2)对比UB和UU结构可以看出,将同等厚度的空气层分配在两侧时,仅在较窄的频段有一点提升,吸声系数的改善并不明显。
(3)针对双层板复合结构,增大薄膜面密度会使吸声系数峰值对应的频率向低频移动,可以改善低频段吸声系数,但在高频段的吸声系数会降低。
附录A
图A1为BB布局计算实例示意图。
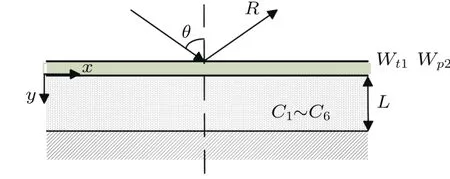
图A1BB结构算例Fig.A1 Example of BB structure
边界条件如下:
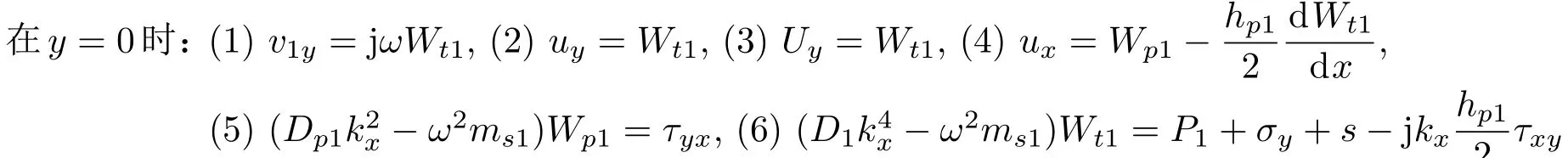
在y=L时:(7)uy=0,(8)Uy=0,(9)ux=0。
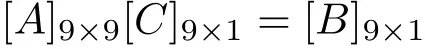
其中,[C]T=[C1C2C3C4C5C6Wt1Wp2R]。

其余全为零。
