一种加权的深度森林算法
2019-04-01宫振华王嘉宁
宫振华 王嘉宁 苏 翀*
1(南京机电职业技术学院 江苏 南京 211135)2(江苏科技大学电气与信息工程学院 江苏 苏州 215600)
0 引 言
现时,深度学习网络模型取得了长足的进步和发展,这一切要得益于大数据时代的到来。虽然深度学习网络模型为数据分析提供了有力的工具,但其所具有的大量调解参数和复杂的网络结构都在一定程度上决定了模型的学习效果。此外,由于深度学习网络模型在训练时需要大量的训练样本,因此,整个过程既耗时又对设备有较高的要求。而深度森林DF是一种基于深度模型提出的级联随机森林方法,它具有较少的调节参数,允许使用者可以根据设备的资源决定训练的耗费,并能自适应地调节训练模型层数。文献[1]的实验结果充分表明,相较于深度学习网络模型,深度森林取得了更好的分类性能。在结构层面,深度森林由多粒度扫描和级联森林两个部分组成[1]。其中,多粒度扫描通过滑动窗口技术获取多个特征子集,以增强级联森林的差异性。级联森林则是将决策树组成的森林通过级联方式实现表征学习。可以说,深度森林沿用了深度学习对样本特征属性的逐层处理机制,利用多级结构实现表征学习。与深度学习不同之处主要表现在以下几个方面:
(1) 深度森林的级数是随着训练的不断不深入自动调节的;
(2) 深度森林具有很少的超参数且对超参数不敏感;
(3) 深度森林具有较低的训练开销,既适用于大规模数据集,也适用于小规模数据集;
(4) 其结构适用于并行处理。
深度森林在结构上由多级组成,每级分别由随机森林[2]和完全随机森林[3]两种森林组成。就每个样本而言,每个森林将其各个子树预测的类概率向量进行算术平均后,作为该森林的预测结果,并与样本的原始特征向量拼接,作为下一级的输入。由于森林中各个子树的预测精度是各不相同的,算术平均会导致子树的错误预测对整个森林的预测产生影响,进而随着级数增加,有可能使错误被进一步放大。为了避免上述影响,本文提出了一种加权的深度森林WDF(Weighted Deep Forest)。主要思想是根据森林中每棵子树的预测精度计算其相应权重,再对各个子树的预测概率向量进行加权求和,以提高深度森林的预测精度,降低级联级数。
1 深度森林
深度森林与深度神经网络都是通过多级结构进行表征学习[4],但深度森林以其简单的训练模型以及不依赖于大量数据进行训练的特点弥补了深度神经网络的缺点,并逐渐被应用于工程实践中[5-6]。
深度森林由多粒度扫描和级联森林两个部分组成。多粒度扫描主要处理高维数据和图像数据。假设长度为n的一维特征向量,若使用长度为m的窗口进行滑动且每次滑动一个单位长度,将产生n-m+1个具有m维特征向量的数据子集;类似地,对于一个n×n的二维图像数据,若使用m×m的窗口进行滑动,每次滑动一个单位长度,将产生(n-m+1)2个具有m×m特征向量的数据子集。这些数据集将分别输入到1个完全随机森林和1个随机森林。对于c个类别的分类问题,经过两个不同的随机森林分类后,长度为n的一维特征向量将产生长度为2c(n-m+1)的类向量;类似地,对于一个n×n的二维图像数据,将产生长度为2c(n-m+1)2的类向量。随后,这些类向量将被拼接到原始的样本的特征空间里,作为后面级联森林的输入特征。整个多粒度扫描结构如图1所示。

图1 多粒度扫描
级联森林主要由随机森林和完全随机树森林两种森林组成。森林之间通过层级方式形成级联结构。对于每一级森林,首先,训练样本通过k折交叉验证,训练其中各棵子树,与此同时,每棵子树对每个训练样本给出一个预测的类概率向量;其次,将测试样本输入训练得到的森林,每棵子树对每个测试样本也给出一个预测的类概率向量;再次,森林对所有子树预测的类概率向量按训练样本和测试样本分别计算平均类概率向量;最后,该级的所有森林将所有样本上的平均类概率向量与样本的原始特征向量拼接后作为下一级森林的输入特征。每级结束预测后,会在验证集上对预测结果进行评估,以决定是否扩展下一级。如果不再扩展,则在已扩展的级中,找出最优评估结果所对应的级,将所有森林在测试样本上的平均类概率向量算术平均后,取概率最高的类向量作为整个深度森林的预测结果。其中,级联森林结构和单个森林的结构分别如图2和图3所示。

图2 级联森林结构

图3 单个森林结构
2 加权的深度森林
深度森林中各棵子树对应不同的预测精度,简单的算术平均法,忽略了各棵子树之间的预测差异,使预测错误率较高的子树对整个森林的预测结果产生较大影响。为此,本文对森林中各棵子树的结合策略进行改进,提出一种加权的深度森林WDF,其中每个森林的结构如图4所示。
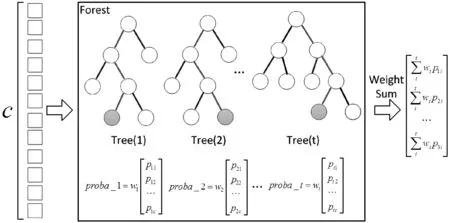
图4 单个加权森林结构
假设训练样本集T和测试样本集S的示例个数分别为m和n,类别标记的个数为c,记为L={l1,l2,…,lc}。设森林F包含t棵子树,记第k棵子树为Tk(k∈[1,t]),第i个训练样本被子树Tk预测为类lj的概率为pij,则在训练样本集T上,子树Tk预测的类概率矩阵如下所示:
(1)
定义函数Max(X)表示获取二维矩阵中行向量X的最大值元素所对应的列下标,当有多个相同的最大值时,取最小的列下标。令列下标从1开始,则子树Tk对训练样本集T的预测结果向量如下所示:
(2)
定义函数Acc(X1,X2)表示两个同维向量X1、X2中相同位置元素相等的个数所占的比例。例如:
令Y(T)是由训练样本集T的真实类映射到类集合中的下标所组成的向量,则子树Tk对训练样本集T的预测准确率ak为:
ak=Acc(Predict(Tk,T),Y(T))
(3)
至此,第k棵子树的权重[7-8]Wk为:
Wk∝log2(ak/(1-ak))
(4)
最后,森林F在训练样本集T和测试样本集S上预测的类概率矩阵分别为:
(5)
(6)
更进一步,假设级联森林中每一级又包含h个森林,那么第e级森林组合Ce在训练样本集T和测试样本集S上预测的类概率矩阵分别为:
(7)
(8)
类似地,如果把上述矩阵改写成行向量组的形式,可分别得到第e级森林组合Ce对训练样本集T和测试样本集S的预测结果向量,具体如下:
(9)
(10)
同理,令Y(T)、Y(S) 分别表示由训练样本集T、测试样本集S的真实类映射到类集合中的下标所组成的向量,则第e级森林组合分别在训练样本集T和测试样本集S上预测准确率Aet和Aes分别为:
Aet=Acc(Predict(Ce,T),Y(T))
(11)
Aes=Acc(Predict(Ce,S),Y(S))
(12)
当级联森林不再扩展时,则在已扩展的级中,找出在训练样本集T上预测准确率最高值所对应的级,将该级森林组合在测试样本集S上预测结果向量和预测准确率作为整个加权深度森林的预测结果。加权的深度森林(WDF)如算法1所示。
算法1加权的深度森林(WDF)
输入 训练集T,测试集S,森林中子树的数目N,每一级森林的数目M
1 ifT是高维数据集 then
2T=多粒度扫描(T);
3 end if
4 for i=1 to M
5 for j=1 to N
6 使用T训练子树;
7 根据式(1)-式(3)计算子树的准确率;
2)市外电源方面,形成了2+X格局:(1)华东电网内的安徽煤电基地,(2)华东电网外的三峡和金沙江等西南水电,并在华东电网内参与建设核电、抽水蓄能等项目。
8 根据式(4)计算当前子树的权重;
9 输入测试集T到当前子树;
10 end for
11 根据式(5)、式(6)分别计算当前森林在训练集T和测试集S上的预测类概率矩阵;
12 end for
13 根据式(7)、式(8)分别计算当前级联森林在训练集T和测试集S上的预测类概率矩阵P;
14 if 评估后继续扩展下一级 then
15 将概率矩阵P拼接到原始特征空间,形成新的训练集T*和测试集S*;
17 else
18 在所有扩展的级中找出训练集上预测准确率最高的那一级opt_lay_id,并输出该级在测试集S预测的结果;
19 end if
对比图2和图4可以发现,加权的深度森林可以利用权重值修正森林的类概率矩阵。当修正的概率矩阵作为下一级的输入时,会使下一级森林在训练过程中不断优化并提高其预测精度,在一定程度上,不仅能提高最终预测精度,还可以减少扩展级数。
3 实 验
本文在高维和低维数据集上分别对深度森林(DF)和加权的深度森林(WDF)进行实验比较。实验平台配置如下:160 GB内存、24核CPU、64位Ubuntu16.04操作系统、Anaconda2(Python2.7)、类库包括Numpy、Scikit-learn、Tensorflow等[9-10]。

3.1 实验数据集
采用文献[1]中所使用的实验数据集,与原文相同,每个数据集的80%用于训练,20%用于验证。参与实验的高维数据集有:GTZAN[11]、SEMG[12]、MNIST[13]以及IMDB[14];低维数据集有:ADULT[15]、YEAST[16]、和LETTER[17],其中,低维数据集无需进行多粒度扫描。参与实验的数据集描述如表1所示。

表1 实验数据集
3.2 实验结果及分析
实验分别采用测试集上的准确率和扩展的级数作为评价指标。具体实验结果如表2所示。

表2 实验结果
从表2可以看出,在低维数据集上,加权的深度森林预测准确率要略高于深度森林,但扩展级数多于深度森林。与此相反的是,在高维数据集上,无论准确率还是扩展级数,加权的深度森林都要优于深度森林。出现这一现象,主要有以下几点原因:
(1) 低维数据集包含的特征数较少,造成了森林中训练得到的子树之间的差异较少,则每棵子树的预测准确率较为接近。从式(4)可以看出,每棵子树的权重也较为接近。因此,其性能提高有限。
(2) 高维数据集往往包含较多的特征数,再经过多粒度扫描处理后,非常有利于增加后续级联森林中训练所得子树之间的差异。由于每棵子树的预测准确率波动较大,最终导致差异较大的权重分布。
由上述分析可知,深度森林中训练得到的子树之间的差异往往决定了最后的预测精度和级联数,而子树之间的差异性却受到数据集中特征数的影响。这与级联森林主要由随机森林和完全随机树森林两种森林组成有关。通过表1和表2可以看出,由于高维数据集上训练得到的子树之间的差异性增加,每棵子树的预测准确率差异也较大,加权的思想会赋予准确率高的子树较大的权重,以增加其在决策中的作用。因此,加权深度森林优势在高维数据集上具有明显的优势,在准确率提高的同时,森林的级联数也有所减少,降低了训练时间;而在低维数据集上,由于权重之间差异性较小,延缓了收敛速度,增加了森林的级联数,虽然增加了训练时间。但与原算法相比,还是获得了可比的性能。综上所述,加权的深度森林更适合利用多粒度扫描处理高维数据集。
4 结 语
深度森林沿用了深度学习对样本特征属性的逐层处理机制,但克服了深度学习参数依赖性强、训练开销大以及仅适用于大数据等不足之处。然而,深度森林中各个子树的预测精度是各不相同的,简单算术平均会导致子树的错误预测,对整个森林的预测产生影响,进而随着级数增加,有可能使错误被进一步放大。为此,本文提出了一种根据森林中每棵子树的预测精度进行加权的深度森林。通过在高维和低维数据集上进行实验,结果表明:加权的深度森林在高维和低维数据集上性能都获得了一定提升,特别在高维数据集上,这一优势较为明显。由于目前所使用的加权方式较为简单,下一步将进一步考虑更为全面的权重评估方式,比如综合集成分类器的多样性和分类性能的权重评估方式等。
