空爆冲击波对不同形状破片的绕流作用仿真分析

郑红伟，陈长海，李 茂，朱 锡，龚 辉

(1. 海军工程大学 舰船工程系，湖北 武汉 430033；2. 东部战区海军参谋部，浙江 宁波 315000)

0 引 言

随着现代武器的迅速发展，对舰导弹成为当今武器研究的热点之一。导弹爆炸产生的冲击波和大量高速破片是联合作用在结构上的2种最主要的毁伤元素[1]。战斗部壳体的材料属性、厚度、装药量、装药类型、壳体形状和起爆方式都对冲击波和高速破片的形成都存在一定的影响[2–5]。早期，国内外学者关于冲击波和高速破片的研究思路大多还是将2种载荷的解耦处理[6–7]，根据冲击波和高速破片在空气中的衰减特性，求解了冲击波在前、相遇以及冲击波在后的3个阶段传播规律[8]，并将二者对结构的毁伤效应解耦成冲击波冲量效应和高速破片穿甲作用2个问题分别研究[9]。但实际在整个传播过程中2种载荷存在着相互影响。在载荷形成阶段，破片的存在会使爆炸产生的一部分能量损耗于高速破片的形成，从而使冲击波的能量减弱[10]。传播阶段，李茂等[11]在研究中指出冲击波遇到破片时存在明显的反射和绕流现象。冲击波传播过程中发生的绕流和反射现象会改变冲击波的超压、比冲量等载荷特性[12–13]，从而改变实际作用于结构的冲击波强度。当前关于冲击波对破片绕流作用的研究还比较少，而破片形状作为影响冲击波绕流作用的主要因素之一，其研究更有必要性。

为分析战斗部空中爆炸后冲击波对高速破片的绕流效应，可以更加真实的反应在传播过程中冲击波和高速破片的载荷特性。本文将采用Ansys/Ls-dyna非线性动力有限元分析软件，对端部预制破片工况进行数值模拟。建立多个计算模型对比分析破片形状因素对冲击波绕流作用的影响。

1 模型建立与仿真方法验证

1.1 模型选择及参数设置

数值模拟采用g-cm-μs单位制，模型由空气域、破片、炸药、钢板4个部分组成。炸药和空气域均采用Euler单元，使用多物质单元ALE算法，预制破片和钢板采用Lagrange单元。空气域的尺寸取500 mm×500 mm×325 mm，模型布置和模型尺寸剖面示意图如图1所示。

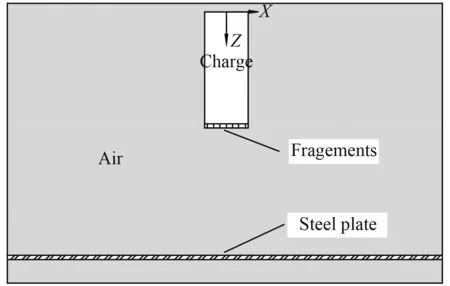
图 1 模型示意图Fig. 1 Schematic diagram of the model

通过关键字*CONSTRAINED_LAGRANGE_IN_SOLID定义破片与空气材料间的耦合算法。保证计算精度，模型网格密度应尽可能高，炸药尺寸与炸药网格尺寸比值至少应大于6[14–15]，但在有限元分析中单元划分越细，节点数目越多，计算步长越短，计算时间越长。为减少计算时间，在保证主要研究区域网格精度的前提下，空气和钢板模型均采用发散性网格，钢板在中心边长140 mm的方形区域内进行细化，细化区域六面体网格边长约为1 mm。最终划分得到空气域单元总数约50万个，炸药单元总数约7万个，钢板单元总数5.6万个。通过试算，确定计算步长因子取0.65。仿真中欧拉域各面均设置无响应边界条件，含钢板结构的仿真工况中钢板采用四边固支的边界条件。

炸药采用*MAT_HIGH_EXPLOSIVE_BURN本构模型，对轰爆产物的膨胀采用*EOS_JWL状态方程来描述：

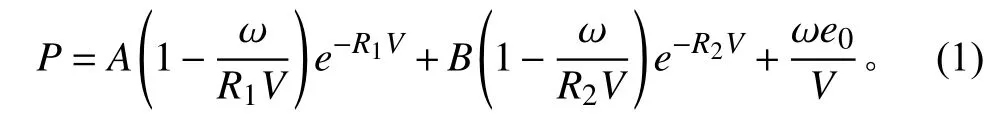
表 1 TNT炸药材料参数及状态方程参数Tab. 1 The materials and EOS parameters of TNT

空气采用*MAT_NULL材料模型及*EOS_LINE AR_POLYNOMIAL状态方程描述。状态方程的线性多项式为：

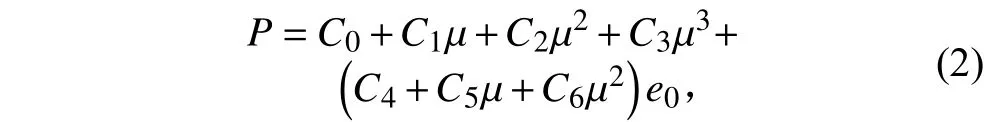
表 2 空气材料参数及状态方程参数Tab. 2 The materials and EOS parameters of air

试验模型中破片采用双线性弹塑性本构模型*MA T_PLASTIC_KINEMATIC，其应变率则由Cowper-Sym onds模型描述，应变方程为：

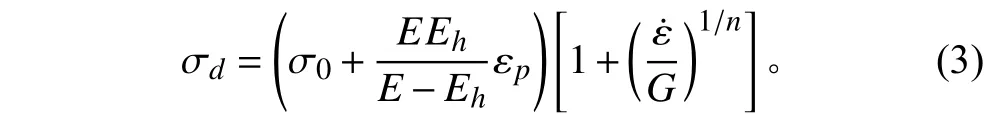
钢板采用Johnson-Cook本构模型，该模型考虑了材料在高温高应变率下的软化效应，能够反映高应变率以及高温情况下材料的性质变化，其状态方程为：

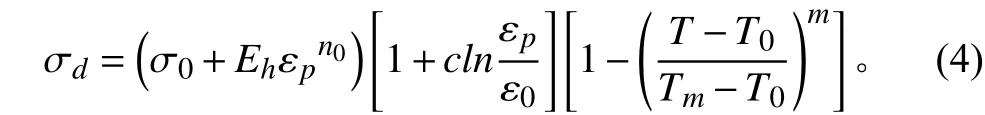
材料的失效则由下述方程描述：

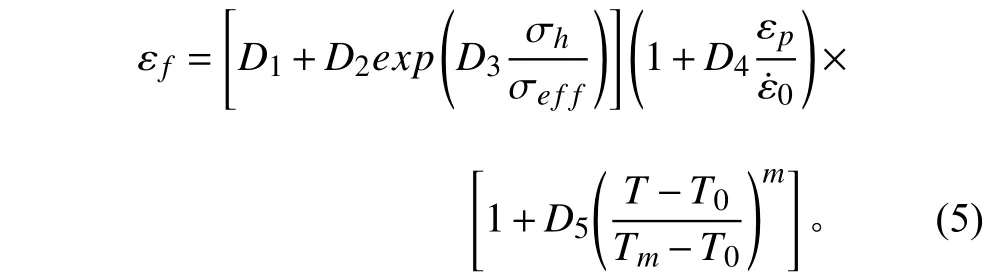
表 3 Q235钢力学参数及方程参数Tab. 3 The materials and EOS parameters of Q235

1.2 仿真方法验证

为验证模型建立的合理性，本文首先对空中近爆冲击波载荷作用下钢板的变形试验[17]（模型1），近爆载荷联合作用下钢板变形毁伤试验[18]（模型2）以及同样装药工况下的2 mm和4 mm的Gurney平板驱动理论模型（模型3、模型4）进行仿真分析。模型中炸药均为两发直径50 mm、高度65 mm的柱形铸装TNT轴向叠加布置，总装药质量400 g。炸药下端面距离平板结构爆距为150 mm，模型1中钢板厚度为4 mm，模型2中钢板和预制破片厚度均为2 mm，破片总数为89枚，总质量为34.9 g，采用对称方式布置（见图2）。

仿真结果如图3所示，模型1中平板的整体挠曲变形在 1 140 μs时趋于稳定，中心最大挠曲变形为 39.5 mm，与试验值42.3 mm相差约为6.6%；模型2中固支方板模型中心处的冲塞破口直径为56.9 mm，与试验值相当，其最大挠曲变形出现在破口附近，仿真值为24.4 mm，较试验值25 mm小约2.4%；模型3和模型4中平板获得的最终速度仿真结果分别为 1 921.6 m/s，1 206.8 m/s 较Gurney 平板抛掷公式[19]预测结果 1 851.7 m/s，1 246.4 m/s相差分别为3.8%，2.8%。通过以上比较，可知该仿真方法及选取的模型参数较为合理。

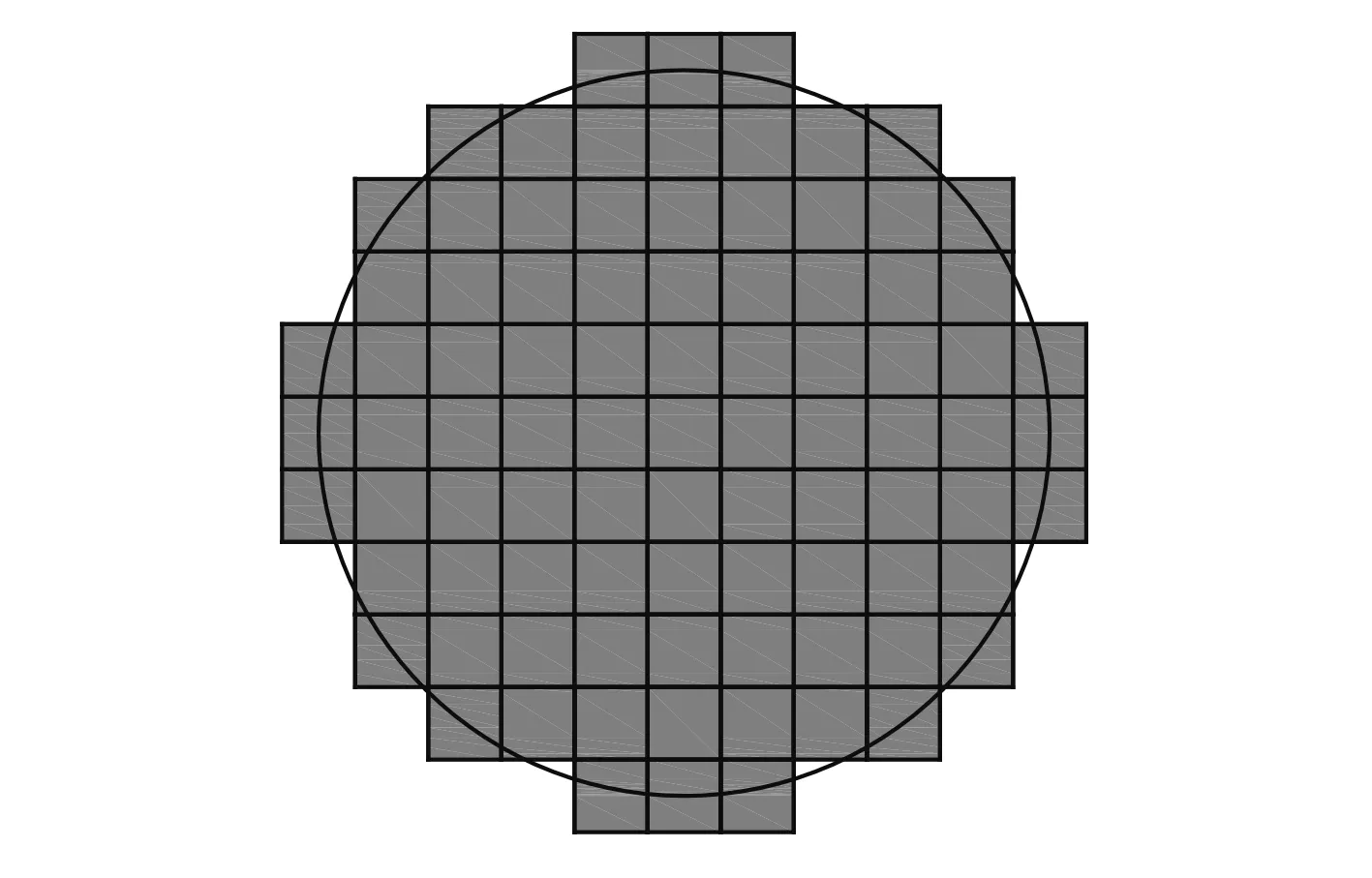
图 2 模型 2 预制破片布置图Fig. 2 Placed fragments of model 2

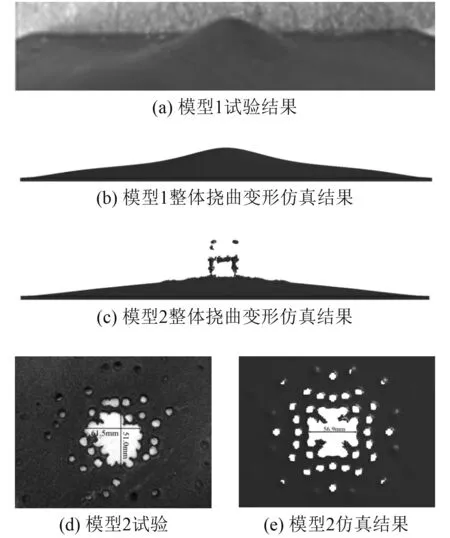
图 3 试验结果与模型仿真结果Fig. 3 Experimental and numerical simulation images of damaged steel plate

1.3 计算工况

为分析比较爆炸产生的冲击波对不同形状高速破片绕流作用的差异，在同等装药条件下，通过变化预制破片形状，研究破片形状对冲击波绕流作用的影响规律。本文建立了厚度为2 mm的圆形、三角形和不同长宽比的方形预制破片工况进行仿真计算，具体模型参数如表4所示，破片形状及布置方式如图4所示。

根据文献[17]可知，在150 mm近爆工况中钢板的碟形变形区为半径为125 mm的圆形区域，可以认为该圆形区域为冲击波载荷的主要作用区域。故在距离炸药预制破片端150 mm水平位置选取测量区域。取圆心在轴线上，半径R=25 mm的圆形区域为测量区域1，半径R=125 mm的圆形区域为测量区域2（见图5），读取测量区域1内的冲击波平均超压数值和测量区域2内的比冲量平均值进行分析比较。

表 4 计算工况Tab. 4 Computational conditions

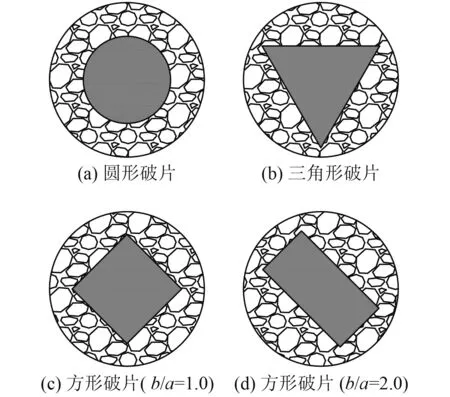
图 4 不同形状预制破片Fig. 4 Fragment in different shape

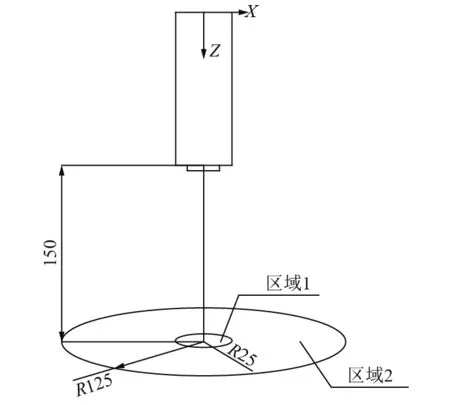
图 5 测量区域分布Fig. 5 View aera

2 计算结果分析

2.1 破片形状对冲击波传播形态的影响

2.1.1 圆形破片

图6为9.81 g圆形破片模型case-3的冲击波压力云图。

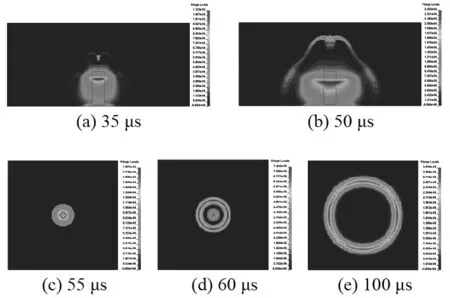
图 6 case-3 冲击波压力云图Fig. 6 Pressure contours of the case-3

从图中可以看出，当破片为圆形破片时，冲击波从两侧绕流至破片之前汇聚合成新的冲击波向前传播，碰撞的冲击波在对称轴线上存在叠加增强效应，压力最大值出现在冲击波碰撞交汇处。绕流冲击波为单凸起波头，通过150 mm爆距截面上的冲击波载荷始终保持圆环形波形，随时间由内沿径向向外扩展，且越向外扩展冲击波强度越弱。

2.1.2 三角形破片

图7为9.81 g三角形破片模型case-6在对角面和150 mm爆距截面上的冲击波压力云图。从图7（a）和图7（b）的对角面压力云图中可以看到，当破片为三角形破片时，冲击波从三角形边长中点绕流的冲击波明显比三角形端点附近的冲击波绕流速度快。由图7（c）～图7（e）可以看出，冲击波主要从距离对称中心最近的三角形各边中点绕流至破片前，形成3个凸起的波头，并在三角形角中线方向出现对称的叠加增强的高压区域。通过150 mm爆距截面的绕流冲击波载荷呈3个紧靠的高压圆环分布，压力区随时间由内沿径向向外扩展，后方冲击波依然趋于圆环形。

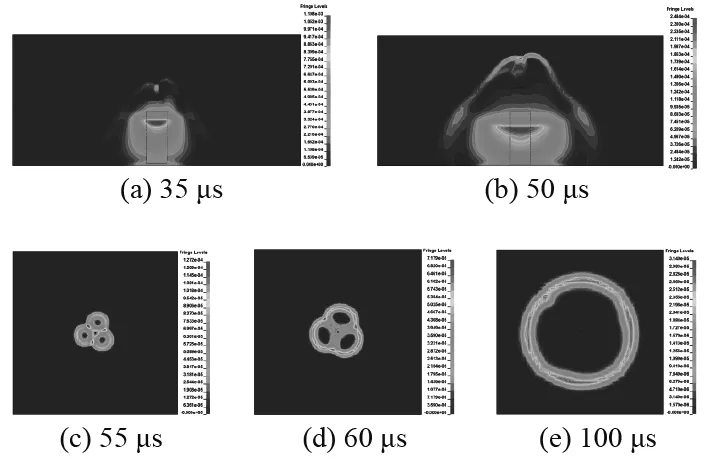
图 7 case-6 冲击波压力云图Fig. 7 Pressure contours of the case-6

2.1.3 方形破片

图8为9.81 g正方形破片模型case-9在对角面和150 mm爆距截面上的冲击波压力云图。从图8（a）和图8（b）的对角面压力云图中可以看到，当破片为正方形破片时，冲击波从破片边缘绕流至破片前传播，在轴线上碰撞加强形成局部的增强区域，其对角面上的绕流冲击波压力云图与圆形破片相接近。由图8（c）～图8（e）可以看出，冲击波主要通过距离对称中心最近的边长中点绕流至破片之前，形成4个凸起的波头。通过150 mm截面上的冲击波载荷呈“田”字形分布，压力区随时间由内沿径向向外扩展，后方冲击波依然为圆环形。

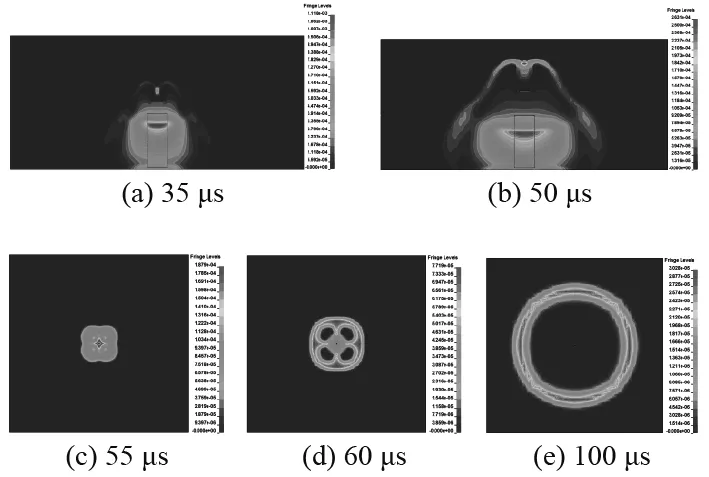
图 8 case-9 冲击波压力云图Fig. 8 Pressure contours of the case-9

图9为长宽比为2.0的9.81 g方形破片模型case-19在对角面和150 mm爆距截面上的冲击波压力云图。图9（a）和图9（b）分别为平行于破片宽边和平行于长边的对角面上冲击波在50 μs时压力云图。从图中可以看到，当方形破片长宽比不为1时，从长边绕流至破片前的冲击波碰撞后形成2个凸起波头，冲击波在平行于长边的对称轴线上形成碰撞叠加的高压区。由图9（c）～图10（e）可以看出，冲击波主要通过距离对称中心最近的长边中点绕流至破片之前，形成2个凸起的波头。通过150 mm截面上的冲击波载荷呈“哑铃”形分布，压力区随时间由内沿径向向外扩展，后方冲击波依然为圆环形。

图 9 case-19 冲击波压力云图Fig. 9 Pressure contours of the case-19

根据上述几个不同形状破片的工况分析可知，不论破片为何种形状，冲击波主要从破片边缘距离破片几何中心最近点处开始绕流。从各边绕流至破片前的冲击波碰撞结合，在合成区域形成叠加增强的高压区，后方冲击波受到破片形状影响较小，依然保持水平圆环形压力区。

2.2 破片形状对绕流冲击波强度的影响

图10（a）为3组不同质量的圆形、三角形、正方形破片在测量区域1的冲击波超压变化曲线，图10（b）为冲击波超压随方形破片的长宽比变化曲线。图中△Pm0为无预制破片的裸药空爆工况case-0在测量区域1的冲击波超压值。由于破片厚度均为2 mm，对于不同形状的等质量破片，其迎爆面面积相同。从图中可以看出，破片尺寸越小，其绕流冲击波超压值越大，越接近△Pm0。质量相同且破片尺寸较大的情况下绕流过三角形破片的冲击波超压值大于圆形和正方形破片工况，而破片尺寸较小时破片形状对绕流冲击波超压影响可以忽略不计。对于方形破片，在保持破片质量和迎弹面积不变的前提下，随破片长宽比的增大，扰流冲击波的超压总体呈增大趋势。这说明方形破片厚度和质量一定时，破片越瘦长，冲击波对其绕流能力越强。

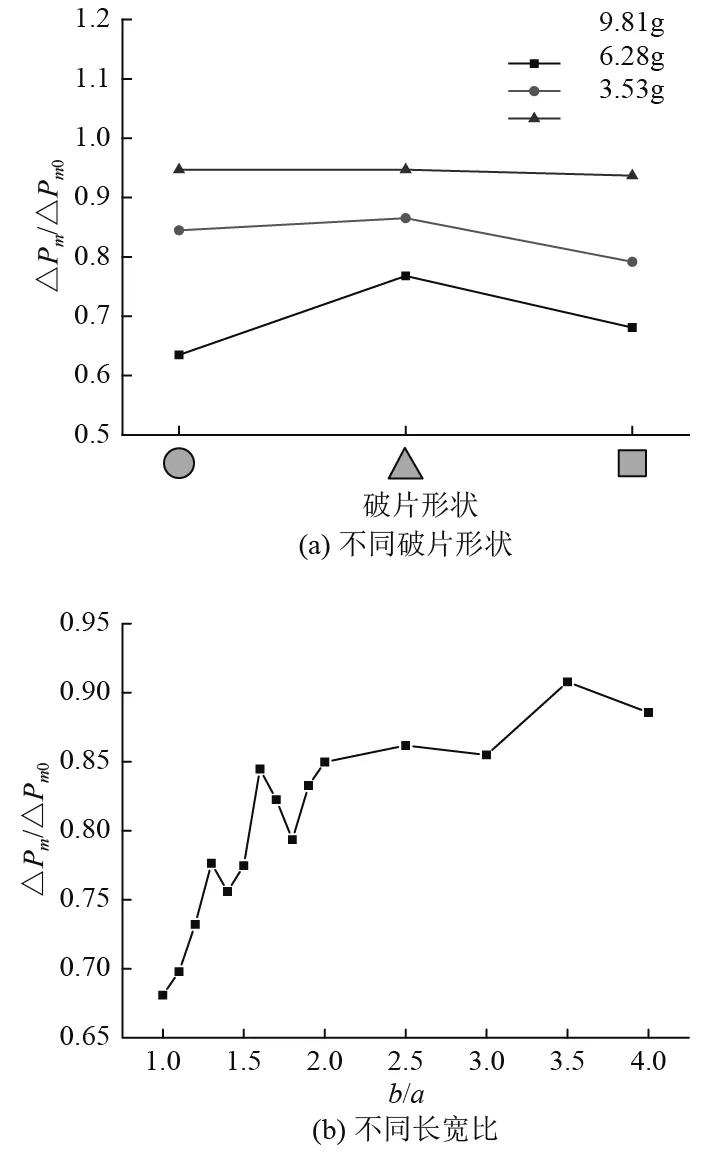
图 10 冲击波超压曲线Fig. 10 Peak over pressure of blast wave

图11（a）为3组不同质量的圆形、三角形、正方形破片在测量区域2的冲击波平均比冲量变化曲线，图11（b）为冲击波比冲量随方形破片的长宽比变化曲线。图中I0为工况case-0中冲击波通过测量区域2的平均比冲量。从图可以看到，等质量的3种形状破片工况的比冲量相差最大不超过6%。绕流过大尺寸破片的冲击波经过测量区域的平均比冲量要低于小尺寸破片工况。图11（b）中随方形破片的长宽比增大，I/I0变化不大，在0.9～1.1之间波动。当破片质量和厚度一定时，破片形状对绕冲击波的比冲量影响不大。

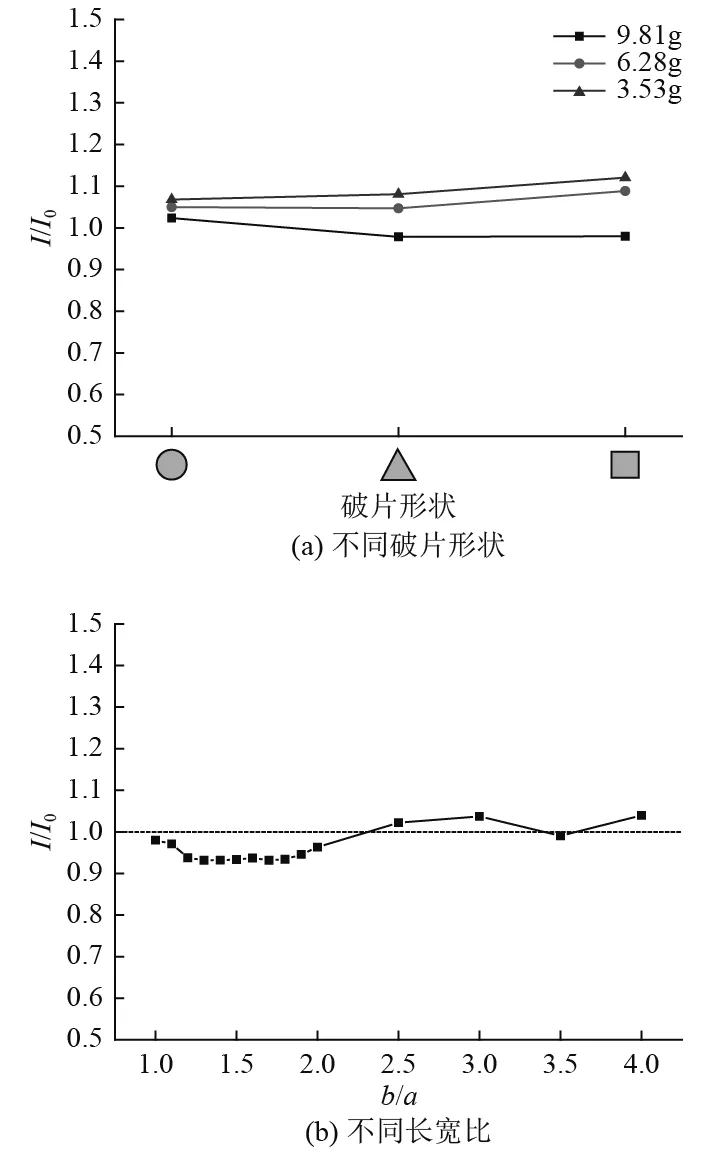
图 11 冲击波比冲量曲线Fig. 11 specific impluse of blast wave

3 结 语

本文利用有限元分析软件Ansys/Ls-dyna计算了实验模型、Gurney平板抛掷模型，验证了仿真模型的可行性。通过对比分析圆形、三角形和不同长宽比的方形破片工况的仿真结果，研究了破片形状因素对冲击波的绕流的影响规律。得到结论如下：

1）冲击波绕流过不同形状破片时，冲击波主要从破片边缘距离几何中心最近处开始处绕流至破片前碰撞形成新的冲击波，破片的形状会影响绕流冲击波前端的波形和作用在结构上的载荷形式。

2）当质量和厚度相同时，冲击波对三角形破片的扰流能力强于圆形和正方形破片，破片较大时其绕流冲击波的超压明显高于圆形和方形破片，而当破片尺寸较小时破片形状对超压影响不明显。

3）当质量和厚度一定时，方形破片越瘦长，冲击波对其绕流能力越强，绕流冲击波超压峰值越大。

4）当质量和厚度一定时，破片形状对绕流冲击波的比冲量影响不大。