一类具有B-D功能反应和Allee效应的非自治捕食系统的渐近性质
2019-03-29李佳美田宝单
李佳美 张 勇 田宝单
(西南科技大学理学院 四川绵阳 621010)
种群生态学是生物数学中的一个重要分支,而捕食者与食饵之间的动力学关系又是种群生态学的中心研究课题之一。通常情况下对一个捕食系统,捕食者为大个体,食饵为小个体。捕食的结果一方面将直接影响食饵的种群数量,另一方面也影响着捕食者的种群变化,两者关系十分复杂。比如在很多捕食系统中,捕食者对食饵捕食的功能反应都依赖于猎物,但在现实中也有许多捕食系统的功能反应依赖于捕食者,特别是对于一些必须通过搜寻食物的捕食者[1],而Beddington-DeAngelis型功能反应(以下简称B-D功能反应):
(1)
就是一种能较好刻画这种捕食关系的功能反应函数[2-3]。B-D功能反应类似于HollingⅡ型功能反应,它可以通过考虑时间的利用或捕食的空间限制来机械地导出,但它在分母中还多了一个额外项,从而更好地模拟了捕食者之间的相互干扰,这种功能反应是由捕食者和猎物共同作用的,并且它还具有与比率依赖形式相同的一些定性特征,避免了一些在低密度下比率依赖模型的奇异行为。
事实上,传统的猎物依赖型和比率依赖型功能反应都可以视为B-D型的极限情况,例如前者可视为c=0的情况,后者则可看成a=0的情况。因此,B-D型功能反应是一种应用更为广泛的功能反应,从而引起了许多生物数学学者的关注。例如,文献[4]研究了一个具有B-D功能反应的非自治捕食系统:
(2)
得到了系统持久生存与灭绝的充分条件、系统周期解存在唯一性、全局渐近稳定性等动力学性质。
另一方面,文献[5]中介绍了以生态学家Warder Clyde Allee命名的一种效应——Allee效应,这种效应对生态学家和数学家来说都是一个非常重要和有趣的现象,其特征在于能更好地描述种群规模或密度与种群平均个体适应度之间的相关性。尽管存在着许多针对Allee效应的生态学机制,但促成Allee效应的促进行为主要包括配偶限制、合作防御、合作性喂养和环境调节等。虽然这些行为可分为不同的类别,但它们可以重叠并且仅在特定条件下才会运行,例如:只有在有捕食者或竞争对手出现时合作防御才会有用。近年来,对Allee理论演化而来的捕食-食饵系统的种群动力学模型的建立和研究备受关注。
基于上述生态学背景,本文建立了下面的一类具有B-D功能反应和Allee效应的非自治捕食系统:
(3)


文章下面的讨论是在如下条件(4)下进行的:
(4)
1 系统的持久生存


当x(0)>0;
当y(0)>0时。

引理2 设(x(t),y(t))T是系统(2)初始值为正的任一正解,则:
(1) ∃T1>0,使得当t>T1时有:x(t)≤M1;
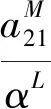

证明:(1) 由系统(2)的第一个方程有

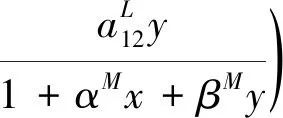
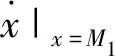
(2) 由系统(2)的第二个方程有

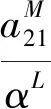

一方面,若y(0)≤M2,则当t≥0时有y(t)≤M2;若y(0)>M2,则∃T2>0,使得当t≥T2时,y(0)≤M2,即总∃T2>0,使得当t≥T2时y(t)≤M2.
定理1 系统(2)若满足条件(3)和下列条件:
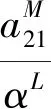
(4)
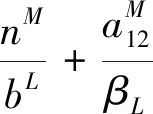
(5)
(6)
则系统(2)将最终一致持久生存,其中
证明:当t≥T时,由系统(2)的第一个方程得:

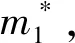

存在当T3≥T1时,使得t≥T3时有x(t)≥m1.
再看系统的第二个方程,当t≥T3时,有
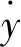
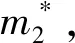

于是∃T4>0,使得t≥T4时总有y(t)≥m2>0 .
取T=max{T1,T2,T3,T4},则t≥T时总有:m1≤x≤M1,m2≤y≤M2.

2 周期解的存在性及全局渐近稳定性
在本节中我们将假设系统(2)的所有参数均为时间t的具有ω周期的正的连续函数,则称对应的系统为系统(2)的ω-周期系统。
定理2 如果周期系统(2)满足式(3)-(6),则系统(2)至少有一个正的周期解。
接下来考虑周期解的唯一性及全局渐近稳定性。
定理3 若ω-周期系统(2)满足式(3)-(6)及下列条件
(7)
则系统有唯一的全局渐近稳定的周期解。
证明:由定理2知系统(2)在满足式(3)-(6)时至少存在一个严格正的周期解,不妨设为U(t)={u(t),v(t)},设X(t)={x(t),y(t)}是系统(2)具有正初始值的任一解。由定理1知,系统(2)任一具有正初始值的解,最终进入K1,因此不失一般性,设U(t),X(t)∈K,t≥0,构造Lyapunov函数:V(t)=|lnx(t)-lnu(t)|+|lny(t)-lnv(t)|,则有:

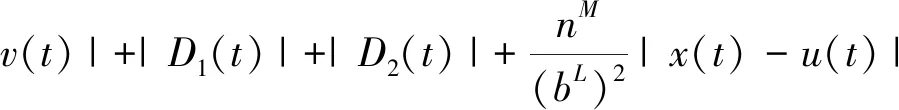
其中
又
|D1(t)|≤

|D2(t)|≤

所以
D+V(t)≤
|x(t)-u(t)|+
由条件(7)知,存在γ>0,使得
D+V(t)≤-γ[|x(t)-u(t)|+|y(t)-v(t)|]即





3 数值模拟
再取两个初值x(0)=25,y(0)=10;x1(0)=40,y1(0)=30,利用Matlab求解作图,结果如图1所示。从图中可以看出,此时系统的两个种群在两组初值条件下都是一致持久生存的,并且随着时间的增大,不同初值条件下的种群密度时间序列最终趋于吻合,这也就进一步佐证了系统周期系统(3)存在周期解,并且该周期解还是渐近稳定的,如图3所示。
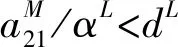

图1 持久生存的数值模拟Fig.1 Numerical simulation of the persistence of the system
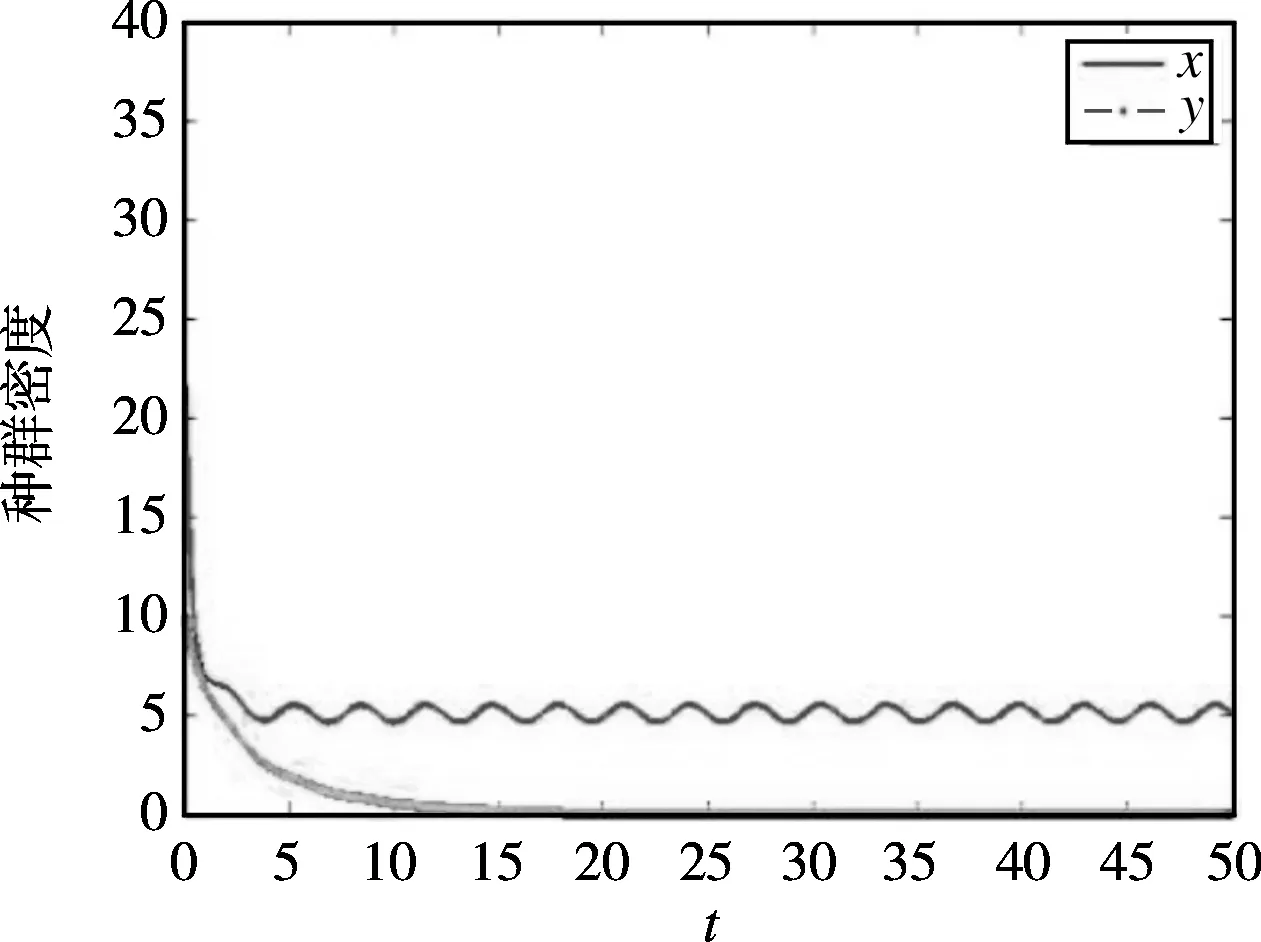
图2 出现灭绝的数值模拟Fig.2 Numerical simulation of the extinction of the predator

图3 周期性数值模拟Fig.3 Numerical simulation of the periodic solution of the system
4 结 论

