PP-ECC墩柱抗震设计方法初探

2019-03-29陈科旭孟庆利单树攀

西南科技大学学报 2019年1期

陈科旭孟庆利张锐单树攀

(1.西南科技大学土木工程与建筑学院四川绵阳 621010 ；2.西南交通大学土木工程学院四川成都 610031)

桥梁是连接各地区的交通枢纽，是生命线工程的重要一环[1]。桥梁在强震作用下发生损坏甚至倒塌，造成巨大的直接经济损失，同时由于交通中断，阻碍了救援队和物资的进入，造成更为严重的间接经济损失[2]。从世界范围来看，桥梁在历次地震下均表现出不同程度的损毁：1971年美国圣费南多发生6.7级地震，由于桥梁抗震能力不足，造成5座桥梁倒塌42座桥梁损坏的严重后果；1995年日本阪神发生7.2级地震，共造成320座桥梁损伤，其中有27座桥梁严重损坏，同时造成神户地区几乎所有交通线路瘫痪[3]。我国是个地震多发国家，1978年我国唐山发生7.8级大地震，桥梁几乎损毁殆尽，造成交通线路完全瘫痪；2008年四川汶川县发生8.0级特大地震，造成建筑、公路、隧道、桥梁严重损毁，其中桥梁损毁尤为严重[4]。

墩柱是桥梁的主要抗侧力构件，因此在各类桥梁损伤(支座、伸缩缝、挡块、桥台、墩柱等损坏)中，墩柱的损伤往往是最为严重的。例如2008年汶川地震中，百花大桥出现墩底损伤，回澜立交的匝道桥墩出现严重损坏[4]。墩柱的破坏往往集中在塑性铰区，究其原因，墩柱塑性铰区强度和延性的不足是导致墩柱破坏的主要因素[5]。混凝土的脆性本质导致在墩柱发生大变形时塑性铰区发生脱落、酥碎，从而限制了墩柱延性的提高。为了有针对性地提高桥墩的抗震性能，目前研究的方向逐渐从改进传统RC墩柱设计方法向使用新材料方面转变[2,6]。

与传统混凝土相比，工程水泥基复合材料(ECC)以2%～3%体积比的纤维来取代粗骨料，具有优秀的延性特性，其峰值抗压应变和极限抗压应变有明显提高，其极限拉应变可达2.5%以上并伴随着细微裂缝的产生出现多缝开裂现象，最终形成了类似金属材料拉伸下的准应变硬化(Pseudo Strain-hardening)特性[6]。在ECC本构关系相关研究方面，ECC材料的单调拉伸、压缩荷载下的本构关系模型和有限元模拟近年来已取得了部分进展[7-9]；在ECC应用于结构构件方面，经过近年大量的研究分析(例如应用在柱子和梁柱节点中的研究)表明，使用ECC的结构构件不仅有更好的损伤容限[6]，较高的抗剪承载力，还可起到箍筋横向约束的作用替代部分箍筋，并使结构构件表现出更好的延性特征。PP-ECC(Polypropylene Fiber Reinforced Engineered Cementitious Composites，聚丙烯纤维工程水泥基复合材料)作为一种基于微观力学设计的超强韧性乱向分布短纤维增强水泥基复合材料，是近年来兴起的新型工程水泥基复合材料[6]。由于PP-ECC较普通混凝土所具备的较大的应变和开裂控制能力使其成为替代桥墩塑性铰普通混凝土的理想材料。

本文针对塑性铰区采用PP-ECC的PP-ECC墩柱进行了抗震性能探索，提出针对PP-ECC墩柱的抗震设计方法，可供墩柱抗震设计及工程实践参考。

1 PP-ECC墩柱的设计计算公式

由于PP-ECC相较于普通混凝土具有显著的高延性特征，所以需要针对PP-ECC墩柱(将RC墩柱的塑性铰区混凝土置换为PP-ECC)推导其设计公式，具体工作如下：基于平截面假定(由于PP-ECC材料无论从材料组分、材料力学性能上说都可认为是一种特殊的混凝土，并且PP-ECC具备多缝开裂、高延性等特征，相比于普通混凝土具备更好的黏结、协同工作能力，因此，PP-ECC墩柱可类比于RC墩柱应用“平截面假定”进行推导)，首先推导了其塑性铰区截面弯矩-曲率曲线关键点的计算方法，然后推导了PP-ECC墩柱力-位移曲线关键点的计算方法。

1.1 基本假定

针对PP-ECC墩柱塑性铰区截面的设计计算作如下假定：

(1)截面应变保持平面；

(2)考虑PP-ECC的抗拉强度；

(3)纵向钢筋的应力-应变曲线模型采用理想弹塑模型；

(4)参考文献[10]等关于PP-ECC的单轴力学性能试验结果，本文认为PP-ECC的一维本构关系模型可近似符合下列关系：

1)受压应力-应变关系(图1)：

上升段：

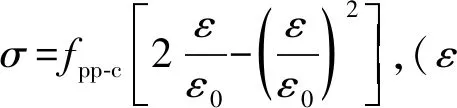
(1)

下降段：

(ε0≤ε≤εu)

(2)

式中，fpp-c为峰值应力，ε0为峰值应力对应的应变，fpp-u为极限应力，εu为极限应力对应的应变。

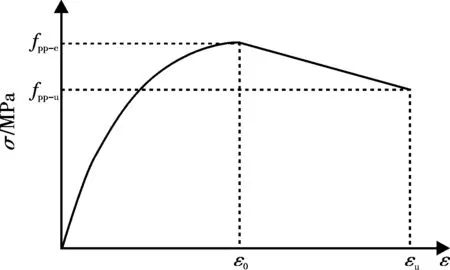
图1 PP-ECC单轴受压本构关系Fig.1 PP-ECC uniaxial compression constitutive relation

2)受拉应力应变关系(图2)：

(3)

应变强化段：

(εto<ε<εtu)

(4)

式中，fpp-to为材料屈服应力，εto为屈服应力对应的应变，fpp-tu为材料极限应力，εtu为极限应力对应的应变。

图2 PP-ECC单轴受拉本构关系Fig.2 PP-ECC uniaxial tensile constitutive relation

1.2 墩柱截面受压区等效矩形应力系数

RC构件在截面受压区混凝土进入非线性状态时，其应力图表征为弧形曲线，为简单快速地求解钢筋混凝土截面的承载力，引入受压区等效矩形应力图[11]，从而通过简单的代数运算求出截面承载力。类比于RC构件，PP-ECC墩柱也可得到相应的等效矩形应力系数。等效的原则是：

(1)PP-ECC压应力的合力大小相等；

(2)图形中受压区合力的作用点不变。

PP-ECC墩柱截面等效矩形应力系数α1和β1仅与PP-ECC应力-应变曲线形状有关，其中α1是受压区PP-ECC等效矩形应力图的应力值与PP-ECC轴心抗压强度fpp-c的比值，β1是受压区PP-ECC等效矩形应力图的高度值与受压区理论高度xc的比值，如图3所示。

图3 等效矩形应力图Fig.3 Equivalent rectangular stress diagram

1.3 墩柱正截面弯矩-曲率曲线关键点计算公式

1.3.1 屈服弯矩

受拉区最外层钢筋达到屈服应力fy时，认为截面进入初始屈服状态，墩柱屈服时的计算模型如图4所示。

为了简化计算，得到实用的设计计算公式，采用条带法计算混凝土受压区的应力值。现就图4墩柱的截面尺寸及配筋情况举例说明墩柱屈服弯矩的计算方法。

图4中截面长宽方向尺寸都为a，混凝土受压区高度为x，条带宽度为b；不同种类的钢筋由于弹模基本相同，根据fy=Esεy，将钢筋的应变比简化为应力比，因此纵筋从左向右应力及面积值依次为fy，As1；f2，As2；f3，As3；受压区混凝土中，PP-ECC应力值用fci表示，hi为纵筋至PP-ECC外表面的距离；受拉区的PP-ECC由于此时所进入的材料应变硬化程度不高，可认为其拉应力不变，均为PP-ECC受拉屈服应力fpp-to；N为墩柱所受的竖向轴力。

根据计算模型图，由力的平衡条件得：

F1A1=F2A2

(5)

F1A1=fyAs1+f2As2+f3As3+

fpp-to(a-x)+N

(6)

F2A2=fc1ab+fc2ab+fc3ab+fc4a(x-3b)

(7)

图4 屈服弯矩计算模型图Fig. 4 Yield moment calculation model diagram

由力矩的平衡条件得：

(8)

受拉区钢筋及受压区PP-ECC的应力值可以根据“截面应变保持平面”的假定，按照几何关系当受拉区钢筋达到屈服应变时计算得出,若计算出的“x-3c”大于c，则需要调整条带的数量及受拉区钢筋的排数重新计算。

1.3.2 屈服曲率

屈服曲率计算图如图5所示。当墩柱柱底受拉区钢筋首次屈服时，即认为墩柱达到屈服状态。此时柱底的截面曲率φy称为屈服曲率，用公式表达为

(9)

其中，φy为屈服曲率，εy为纵筋屈服应变，xy为受拉边缘纵筋到截面中和轴的距离。

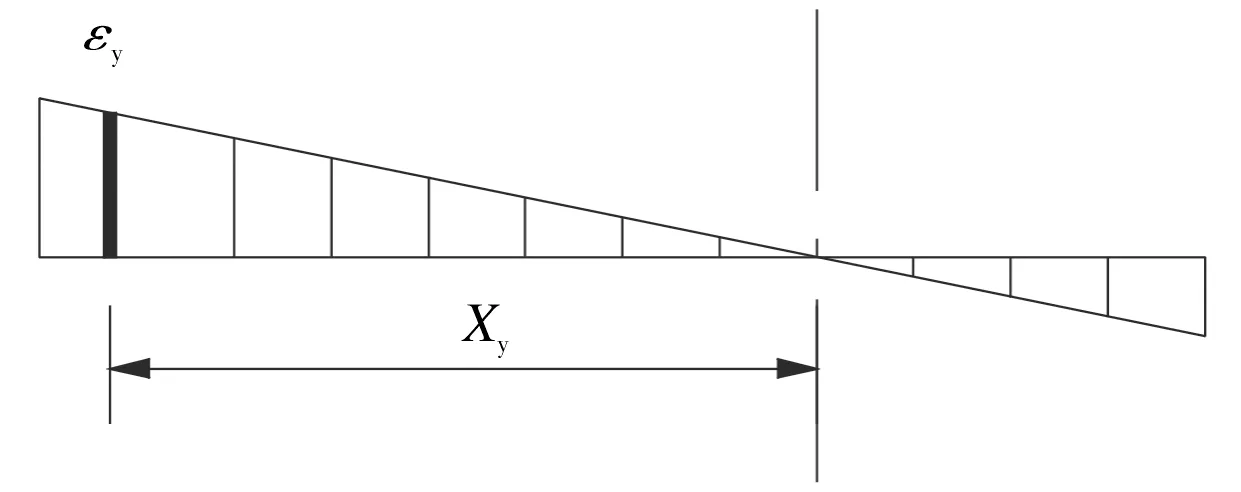
图5 屈服曲率计算图Fig.5 Yield curvature calculation diagram

1.3.3 峰值弯矩

在墩柱屈服之后，最外层受拉纵向钢筋进入流幅状态，中和轴明显上移，受压区PP-ECC应力逐步增大，当受压区最外层达到极限压应变εcu时，墩柱柱底弯矩达到峰值[11]。此时受压区应力分布按1.2节的推导结果等效为矩形，受拉区外缘的PP-ECC已进入强应变硬化阶段，可认为受拉区边缘PP-ECC的拉应力为fpp-tu，如图6所示。

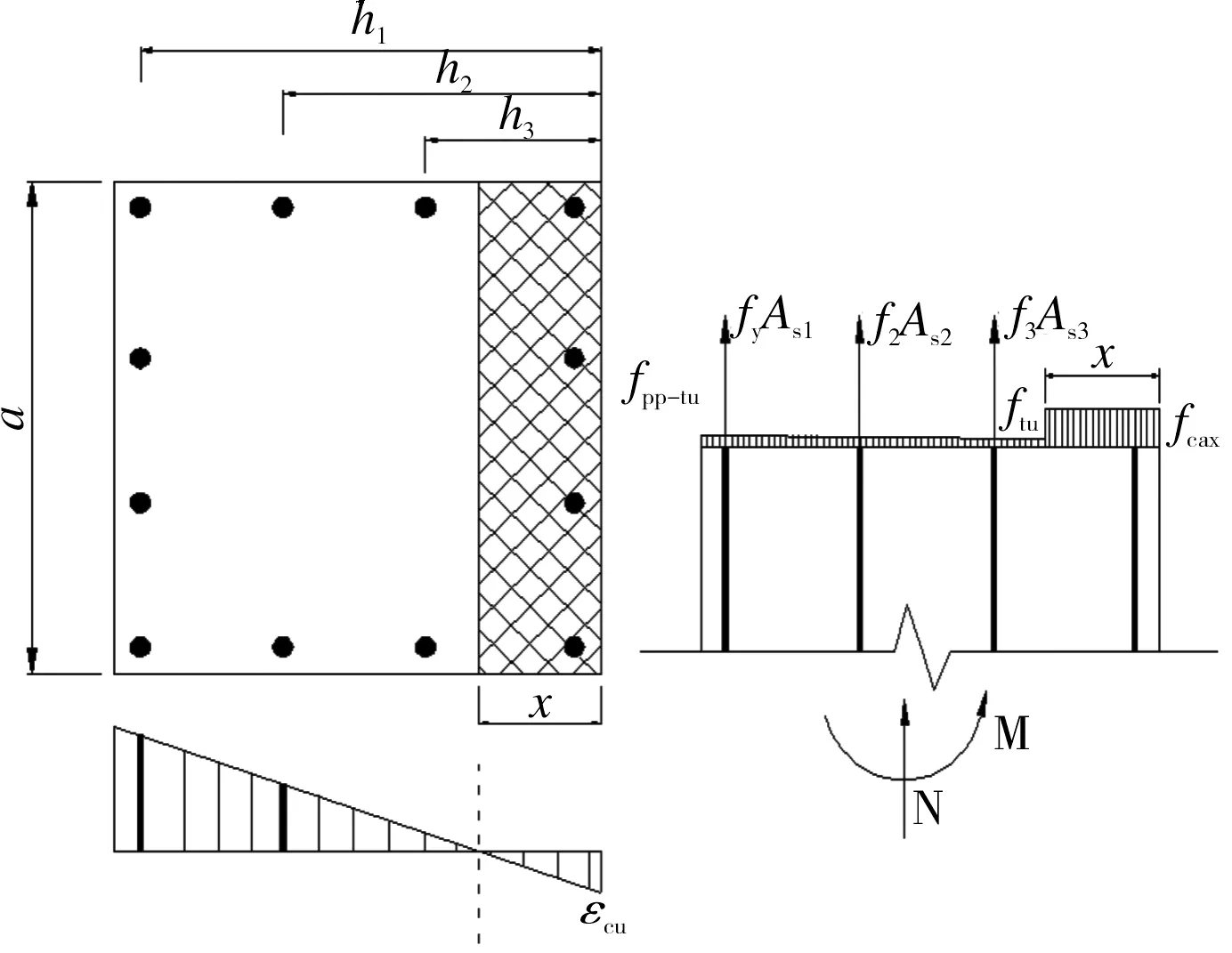
图6 极限弯矩计算模型图Fig.6 Calculation model diagram of ultimate bending moment

就图6墩柱的截面尺寸及配筋情况举例说明墩柱极限弯矩的计算方法。图6中的符号意义同图4，根据计算模型图，由力的平衡条件得：

F3A3=F4A4

(10)

F3A3=fyAs1+f2As2+f3As3+

(11)

x=β1xc

(12)

F4A4=α1fpp-cax

(13)

由力矩的平衡条件得：

(14)

1.3.4 峰值曲率

峰值曲率计算图如图7所示。峰值曲率对应于截面的峰值弯矩，此时截面的承载力达到最大，截面进入强非线性状态。峰值曲率用公式表达为：

(15)

其中，φu为峰值曲率，εu为PP-ECC的极限压应变，xu为受压区最外层到截面中和轴的距离。

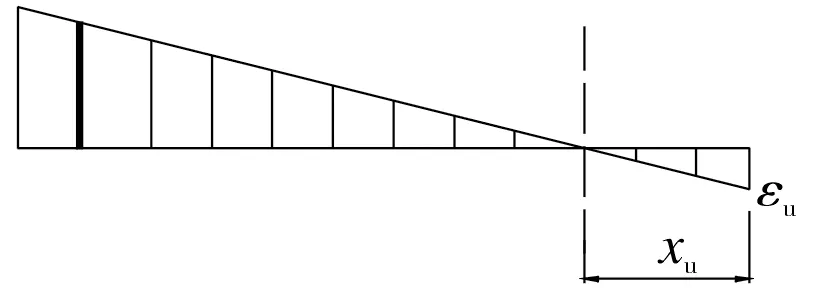
图7 峰值曲率计算图Fig.7 Calculation diagram of peak curvature

1.4 PP-ECC墩柱力-位移曲线关键点计算公式

1.4.1 屈服承载力

(16)

式中，Fy代表墩柱屈服承载力，My代表柱底截面屈服弯矩，L代表墩柱计算长度。

1.4.2 屈服位移

墩柱最外层受拉纵筋达到屈服应变前墩柱基本处于线弹性状态，屈服位移可以认为是最大弹性位移。屈服位移的计算公式可由墩柱在弹性状态下的积分得到[12]，如式(17)所示：

(17)

式中，H为墩柱的有效高度(弯矩最大截面到反弯点的距离),φy意义同式(9)。

1.4.3 峰值承载力

(18)

式中，Fu代表墩柱峰值承载力，Mu代表柱底截面峰值弯矩，L代表墩柱计算长度。

1.4.4 峰值位移

墩柱最外层受拉钢筋屈服后进入非线性状态，柱底塑性铰开始出现(假定PP-ECC墩柱的等效塑性铰长度lpp与RC墩柱一致)，当墩柱达到峰值承载力时对应的位移称之为峰值位移Δu，此时柱顶位移由屈服位移Δy和塑性位移Δp两部分组成[10]，即

Δu=Δy+Δp

(19)

式中Δy为柱顶屈服位移可由式(17)得到；Δp为柱顶塑性位移，可由式(20)得到：

(20)

式中φp=φu-φy为塑性曲率，φu为峰值曲率；lpp为等效塑性铰长度，依据文献[13]《公路桥梁抗震设计细则》可由式(21)和式(22)计算。

lpp=0.08H+0.022fyds≥0.044fyds

(21)

(22)

式中，fy和ds分别为纵筋抗拉强度标准值和纵筋直径；b为矩形截面短边尺寸或圆形截面直径。

2 PP-ECC墩柱设计方法

对于新建PP-ECC墩柱(塑性铰区采用PP-ECC)，其设计过程可按如下步骤进行：

(1)确定墩柱的基本设计参数。墩柱的高度H、轴压比、PP-ECC单轴本构、混凝土强度、纵向钢筋和箍筋强度等。

(2)确定墩柱的设计荷载。根据墩柱所处地区的抗震设防烈度结合抗震规范可确定相应小、中、大震的加速度峰值，由此得到墩柱所应具有的抗力和变形限值。

(3)由以往设计经验初步估算墩柱截面尺寸，从而根据力和力矩的平衡方程式(10)-式(14)，计算得出墩柱纵向钢筋的种类和数量；根据公式(21)和式(22) 计算得出墩柱塑性铰长度lpp。

(4)依据步骤(3)中的截面设计情况可求得柱底截面的峰值弯矩Mu和塑性铰长度lpp，从而根据1.4节公式(18)和式(19)求得墩柱峰值承载力Fu和峰值位移Δu，若不满足步骤(2)的要求则重复过程步骤(2)-步骤(4)，直到满足步骤(2)的要求。

(5)箍筋数量及加密区高度等构造要求按文献[13]计算确定。

3 PP-ECC墩柱模型的设计参数计算

为探究PP-ECC墩柱与普通RC墩柱在承载力、延性等方面的差异，依据本文3.1节所做的PP-ECC(抗压强度fpp-c=30 MPa)单轴力学性能试验结果，拟分别设计制作一个PP-ECC墩柱模型和一个塑性铰区为同等强度混凝土(抗压强度fc=30 MPa)的RC墩柱模型进行伪静力试验。在试验前对上述墩柱模型的各项设计参数(柱底截面弯矩-曲率曲线关键点值、墩柱力-位移曲线关键点值)进行计算分析。

墩柱模型参数如下：高1 200 mm,其截面尺寸为300 mm×300 mm，保护层厚度为10 mm，纵筋采用12根直径12 mm的三级钢(HRB400),箍筋采用直径2.5 mm的冷拔钢丝，设计塑性铰区高度为400 mm，塑性铰加密区间距20 mm，非加密区间距40 mm，柱顶荷载为200 kN。拟采用的普通混凝土强度fc和PP-ECC强度fpp-c均为30 MPa，其中PP-ECC材料本构由3.1节试验给出，普通混凝土本构由文献[14]给出。墩柱三维计算模型如图8所示。

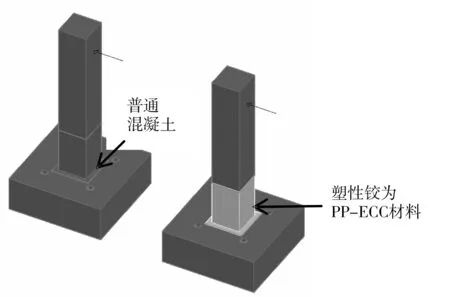
图8 RC墩柱模型与PP-ECC墩柱模型Fig.8 RC Pier column model and PP-ECC Pier column model

3.1 PP-ECC单轴力学性能试验

本节开展了PP-ECC的单轴力学性能试验，包括单向拉伸和单向压缩试验，然后将PP-ECC的单轴力学性能试验结果(ε-δ试验曲线)按1.1节(4)中提出的PP-ECC一维本构关系模型进行拟合。试验过程、试验数据及其拟合结果如图9-图11所示。

基于单轴受压试验的拟合结果(图12，图13)，结合1.2节中截面受压区矩形应力系数的等效原则可得到PP-ECC墩柱截面的受压等效矩形应力图系数为α1=0.8，β1=0.9244，这是3.2节计算的基础。

图9 PP-ECC材料力学试验Fig.9 Mechanical test of PP-ECC

图10 PP-ECC受压应力-应变试验曲线Fig.10 PP-ECC compressive stress-strain test curve

图11 PP-ECC受拉应力-应变试验曲线Fig.11 PP-ECC tensile stress-strain test curve

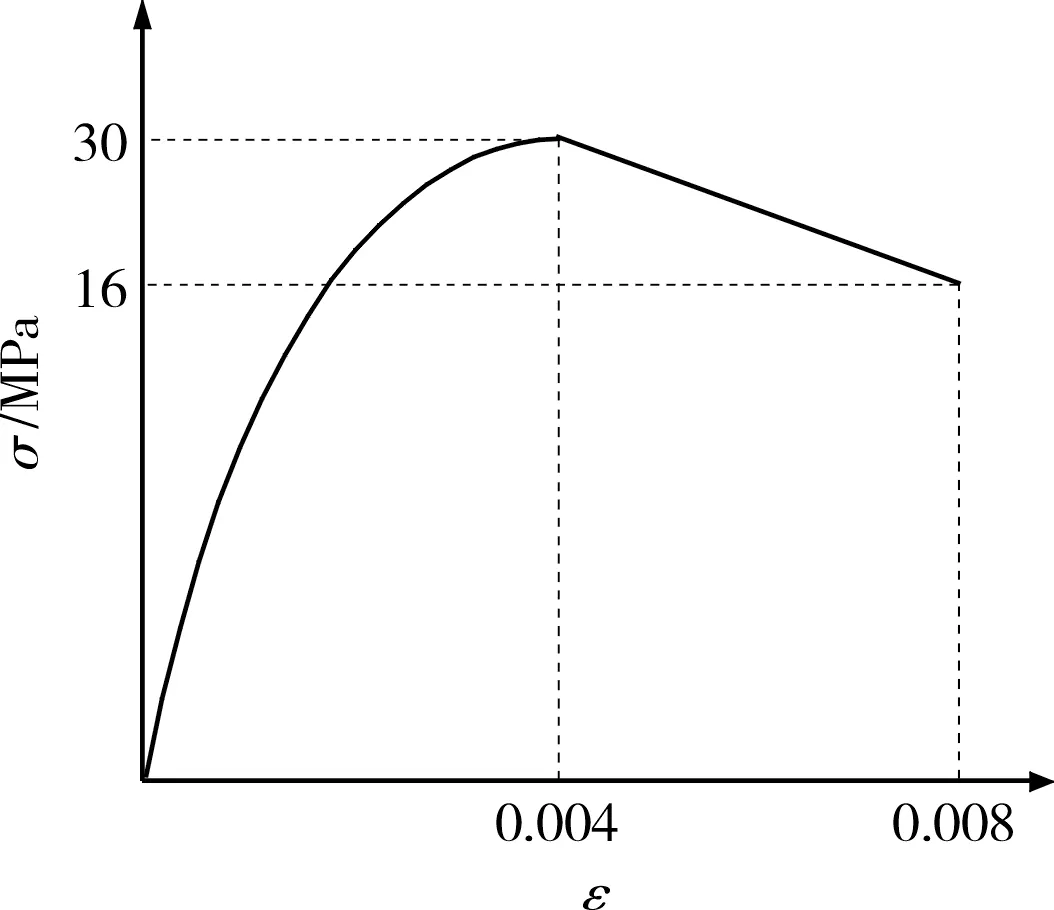
图12 PP-ECC受压应力-应变拟合曲线Fig. 12 PP-ECC compressive stress-strain fitting curve

图13 PP-ECC受拉应力-应变拟合曲线Fig.13 PP-ECC tensile stress-strain fitting curve

3.2 PP-ECC墩柱模型设计参数的计算

根据该墩柱模型截面尺寸、配筋情况及PP-ECC本构关系，由本文第1.3节提出的正截面计算基本公式，可计算出PP-ECC墩柱模型柱底截面弯矩-曲率曲线的关键点值(My，φy，Mu，φu)，并将其与相应的RC墩柱模型进行对比，如表1、表2所示。

根据表1、表2的数据，由1.4节计算公式可计算得出PP-ECC墩柱模型力-位移曲线的关键点值(Fy,Δy,Fu,Δu)，并将其与相应的RC墩柱模型进行对比，如表3、表4所示。

表1-表4中“相对差值”的含义为：(APP-ECC墩柱-ARC墩柱)/ARC墩柱。A为相关参数。

表1 截面弯矩对比Table 1 Comparison of sectional bending moment

表2 截面曲率对比Table 2 Comparison of sectional curvature

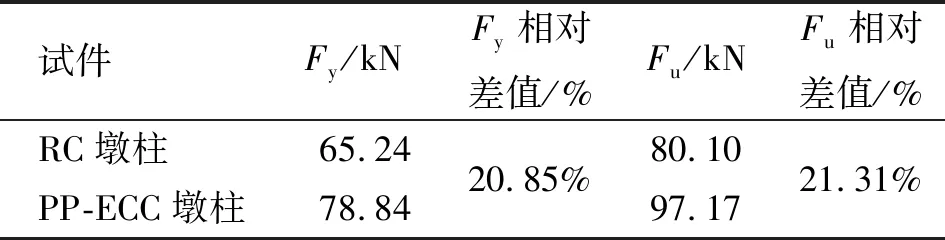
表3 墩柱承载力对比Table 3 Comparison of column top bearing capacity

表4 柱顶位移对比Table 4 Comparison of top displacement

由表1和表3可发现，对于屈服弯矩My、峰值弯矩Mu、屈服承载力Fy和峰值承载力Fu，PP-ECC墩柱均比RC墩柱大20%左右，其原因在于，PP-ECC墩柱柱底截面的受拉区PP-ECC由于具有高极限受拉应变从而能为截面持续贡献拉应力，进而使墩柱截面抗弯承载力有了一定的提高。

由表2可以看出，对于屈服曲率φy，PP-ECC墩柱比RC墩柱提高21.83%；对于峰值曲率φu，PP-ECC墩柱比RC墩柱提高98.79%，几乎达到一倍。由表4可看出，对于屈服位移Δy，PP-ECC墩柱比RC墩柱提高21.77%；对于峰值位移Δu，PP-ECC墩柱较RC墩柱提高幅值达81.71%。这表明，PP-ECC由于自身的高延性、拉伸应变强化等优秀非线性属性，使PP-ECC墩柱也具有高位移延性的特征，表现为PP-ECC墩柱塑性铰截面的变形能力显著提高，从而使PP-ECC墩柱柱顶的屈服位移、峰值位移均较RC墩柱有显著提高。

综上可得，本节针对一方形墩柱模型，塑性铰区采用相同强度的普通混凝土(抗压强度fc=30 MPa)和PP-ECC(抗压强度fpp-c=30 MPa)分别设计了RC墩柱模型和PP-ECC墩柱模型。采用1.3节和1.4节方法计算了墩柱的各项设计参数，结果表明，由于PP-ECC的高延性、拉伸应变硬化等性能，使PP-ECC墩柱较相应的RC墩柱表现为承载力略有提高且峰值位移显著提高。