基于能力设计法的反应谱和时程分析

伏永鹏，郑凯锋，刘云飞

(西南交通大学，四川成都610031)

我国地震多发，需要考虑地震设防的地域辽阔，因此研究结构的抗震性能实属必要。能力设计法(Capability Design Method，CDM)是结构延性设计的主要内容，最早是由新西兰学者Park等人在20世纪70年代中期提出的。该法的定义是：对于结构的非弹性响应设计，首先布置可能出现塑性铰的位置，使结构屈服后形成一个合理的耗能机构；对塑性铰区进行专门的设计，以提供足够的延性，对于其他非塑性铰区，根据塑性铰所具有的超强强度，确定被保护构件的设计强度，从而保证被保护构件在结构塑性铰形成后仍保持弹性［1］。能力设计法的主要优点是可以预定塑性铰出现的位置，而且可以预测结构整体抗震性能。地震作用理论研究是地面运动对结构物产生的动态效应，结构的地震反应取决于地震动和结构动力特性两个方面，桥梁结构地震反应分析的发展过程经历了静力、反应谱、和动态时程三个阶段。静力法将加速度作为结构地震破坏的唯一因素，从动力学角度来看，这种方法忽略了结构的动力反应特性，理论上存在很大局限性。动力反应谱法采用“地震荷载”的概念，从地震动出发求结构的最大地震反应，同时考虑了地面运动特性和结构动力特性之间的关系，比静力法有很大的进步，但是在设计中仍然把地震惯性力视为静力，以弹性分析为主。动态时程分析法以输入合适的地震动为出发点，采用多节点多自由度的结构有限元动力计算模型建立振动方程，然后用逐步积分法对方程求解。计算地震过程中每一瞬时结构的位移、速度、加速度反应，从而可以分析出结构在地震作用下弹性和非弹性阶段的内力变化以及构件逐步开裂、损坏直至倒塌的全过程［2］。

1 公路桥梁抗震设计流程

JTG/T B02-01-2008《公路桥梁抗震细则》(后文简称《抗震细则》)中采用两水平设防，两阶段设计。第一阶段采用弹性抗震设计；第二阶段采用延性抗震设计方法，并引入能力保护设计原则［3］。通过第一阶段的抗震设计，即对应E1地震作用的抗震设计，可达到和原规范基本相当的抗震设防水平。通过第二阶段的抗震设计，即对应E2地震作用的抗震设计，来保证结构具有足够的延性能力，通过引入能力保护构件设计原则，确保塑性铰只在选定的位置出现，并且不出现剪切破坏。

抗震设计采用延性设计理念，延性设计的思想是通过减隔震支座、桥墩塑性铰变形耗能，即大震不倒。与89版《公路工程抗震设计规范》中的三阶段抗震设计思想“小震不坏，中震可修，大震不倒”对比［4］，抗震细则中的E1地震等同于中小震，E2地震等同于大震。常规桥梁抗震设计流程是在E1地震作用下结构在弹性范围内工作，无损伤，验算满足强度要求；如果不满足，调整设计参数，如果满足，则继续在E2地震作用下进行强度和位移的验算。E2地震作用下分为延性构件和能力保护构件，即在延性构件(如桥墩)预设位置出现塑性铰，使结构出现较大的塑性变形，从而使能力保护构件不会发生破坏。其中将桥墩抗剪验算加入能力保护构件，也是考虑强剪弱弯的延性设计理念，即不让桥墩发生剪切脆性破坏。

2 反应谱和动态时程

反应谱分析实际上是一种拟动力分析方法，将结构在动力荷载下的复杂响应情况分解为各阶振型独立的分项响应情况。反应谱设计包括三方面内容：结构各振型的含义和求法；计算各振型反应谱下的结构响应；将各振型结果进行组合。

时程分析是纯粹的动力分析方法，不同与反应谱分析，时程分析法是对结构物的运动方程直接逐步积分求解的动力分析方法，时程分析可得到各质点随时间变化的位移、速度、加速度、进而计算出构件内力的时程变化关系，可以考虑各时间点地震效应情况。对于桥梁结构，地震时程分析分为线性时程和弹塑性时程。弹塑性时程分析需要考虑三方面内容：动力荷载的输入(地震波的选取)；结构弹塑性的考虑方式(塑性铰)；边界非线性的引入(减隔震支座、滑动支座)。

3 反应谱分析

单质点弹性体系在地震作用下的运动微分方程为：2ωξx+ω2，上式为单自由度运动方程，可由 Duhamel积分求解。

体系在t时刻的地震反应为：一般结构阻尼比较小， ωD

结构抗震设计结果由地震响应最大值控制，最大反应之间的关系：Sa=ωSv=ω2Sd。在阻尼比、地面运动确定后，最大反应只是结构自振周期(T，ω)的函数［1］。

单自由度体系在给定的地震作用下某个最大反应与体系自振周期的关系曲线称为该反应的地震反应谱。加速度反应谱是“地震波频率——加速度最大值”关系图，包含了场地特征、阻尼的影响。地震反应谱直接用于抗震设计有一定的难度，它是根据已发生的地震运动记录计算得到的，而工程结构抗震设计需考虑的是将来发生的地震对结构造成的影响。由于地震的随机性和影响地面运动因素的复杂性，即使同一地点不同时间发生地震的地面运动无论强度和频谱绝不会完全相同，因此地震反应谱也将不同。而专门研究可供结构抗震设计用的反应谱，称之为设计反应谱。《抗震细则》规定设计加速度反应谱如下式：

阻尼为0.05的水平设计加速度反应谱S由下式确定：

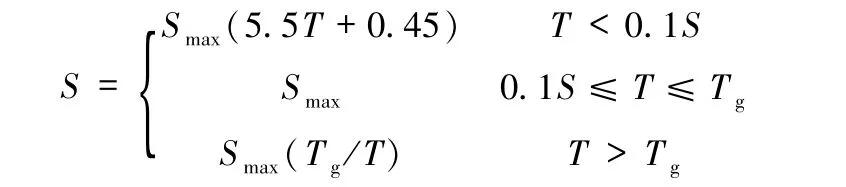
式中：Tg为特征周期(s)；T为结构周期(s)；Smax为水平设计加速度反应谱最大值。

水平设计加速度反应谱最大值Smax由下式确定：

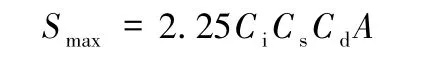
式中：Ci为抗震重要性系数，按表3.1.4-2取值；Cs为场地系数，按表5.2.2取值；Cd为阻尼调整系数，按表5.2.4取值；A为水平向设计基本地震动加速度峰值，按表3.2.2取值［3］。

反应谱法采用振型叠加，由于振型具有正交性，微分方程组可以简化为微分方程，大大减小了计算量，谱函数表示地震加速度与各振型周期间的关系，从而使与时间相关的动力问题，简化为求解各振型下结构施加固定加速度(力)的静力问题。

4 有限元模型计算分析

针对40 m+40 m+40 m的连续刚构桥分别用反应谱和线性时程分析来验算，截面为单箱单室，桥宽9.3 m，墩高10 m，跨中截面如图1所示，桥墩截面如图2所示。该桥所在区域抗震设防烈度为7度，场地类别为Ⅱ类，桥梁类型为A类，特征周期Tg=0.4s，用Midas/Civil建立空间梁单元模型，地基条件良好，故采用墩底固结。结构荷载包括自重、二期、预应力、混凝土收缩徐变和地震作用。

图1 跨中截面(单位：m)

图2 桥墩截面(单位：m)

4.1 反应谱分析

将结构模型的自重和二期恒载转换成集中质量，根据上述参数输入反应谱函数，定义两种反应谱工况分别是顺桥向和横桥向，振型组合方式选择完整二次项组合法(CQC法)，可以考虑周期相近的振型的耦合。

程序提供3种特征值分析方法：(1)子空间迭代法；(2)Lanczos方法；(3)Ritz向量法。子空间迭代法是求解单元数多的大型矩阵特征值问题的常用方法；Lanczos法对于模态较少的特征值分析非常有效；多重Ritz向量法认为结构动态响应是空间荷载分布的函数，考虑空间荷载分布状态及动力贡献，忽略所有反对称振型，对于反对称振型，并不是由荷载激发。荷载在这些振型的动力贡献为零。因此，此处特征值分析方法采用多重Ritz向量法。

结构的前3阶振型如图3～图5所示。

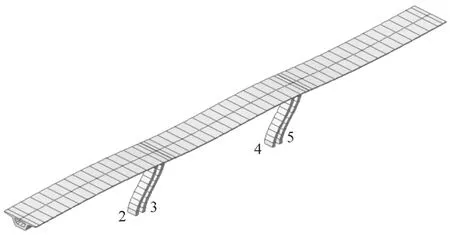
图3 第一阶振型(顺桥向一致平动)

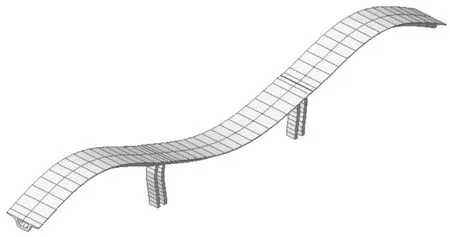
图4 第二阶振型(竖向一阶对称)

进行抗震反应谱分析时，应选择足够的振型数量以保证地震响应的振型参与质量系数之和不小于90%，由多重Ritz向量法计算的顺桥向x，横桥向y，竖向z的振型质量参与系数和分别为99.3%、97.2%、95.2%，因此，此处选取5阶振型满足要求。

E1、E2地震作用下反应谱分析结果：《抗震细则》规定作用效应组合包括永久作用效应+地震作用效应，组合方式应包括各种效应的最不利组合。E1地震作用下的桥墩底部内力见表1，E2地震作用下的桥墩底部内力见表2。

图5 第三阶振型(横桥向一致平动)

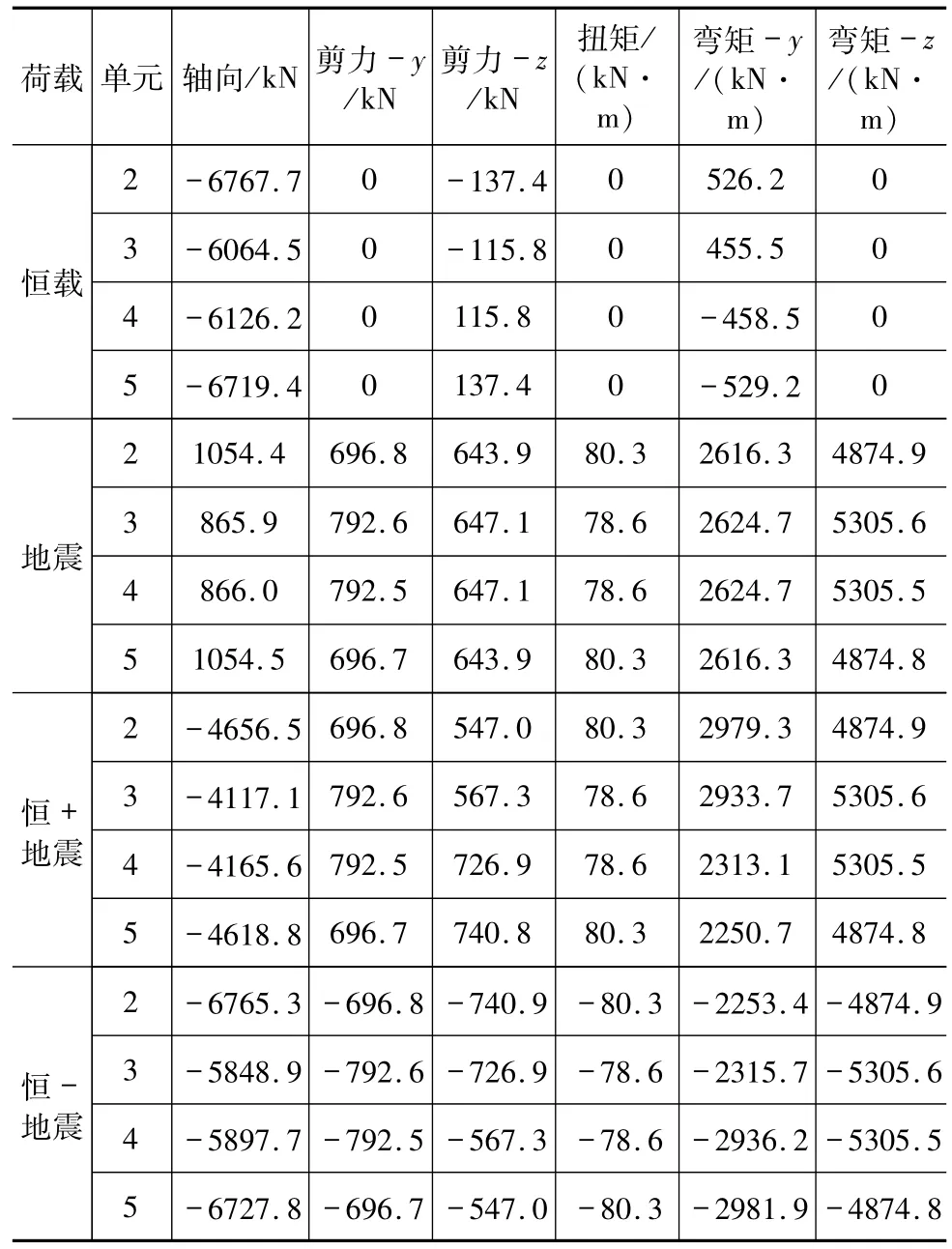
表1 E1地震作用下作用效应组合墩底内力

由于两个方向组合方式是平方和开方法(SRSS法)，反应谱计算结果都为正值，所以偶然组合中由两个组合，即加一次反应谱结果，减一次反应谱结果。

基于《抗震细则》的桥墩验算：E1地震作用下桥墩底部满足强度验算，说明桥墩仍处于弹性状态，再进行E2弹塑性验算(由M-φ曲线对刚度折减)，需要进行桥墩抗剪和位移验算，构件截面的弹塑性由M-φ曲线体现。无约束混凝土和约束混凝土用mander模型，钢材用双折线模型。

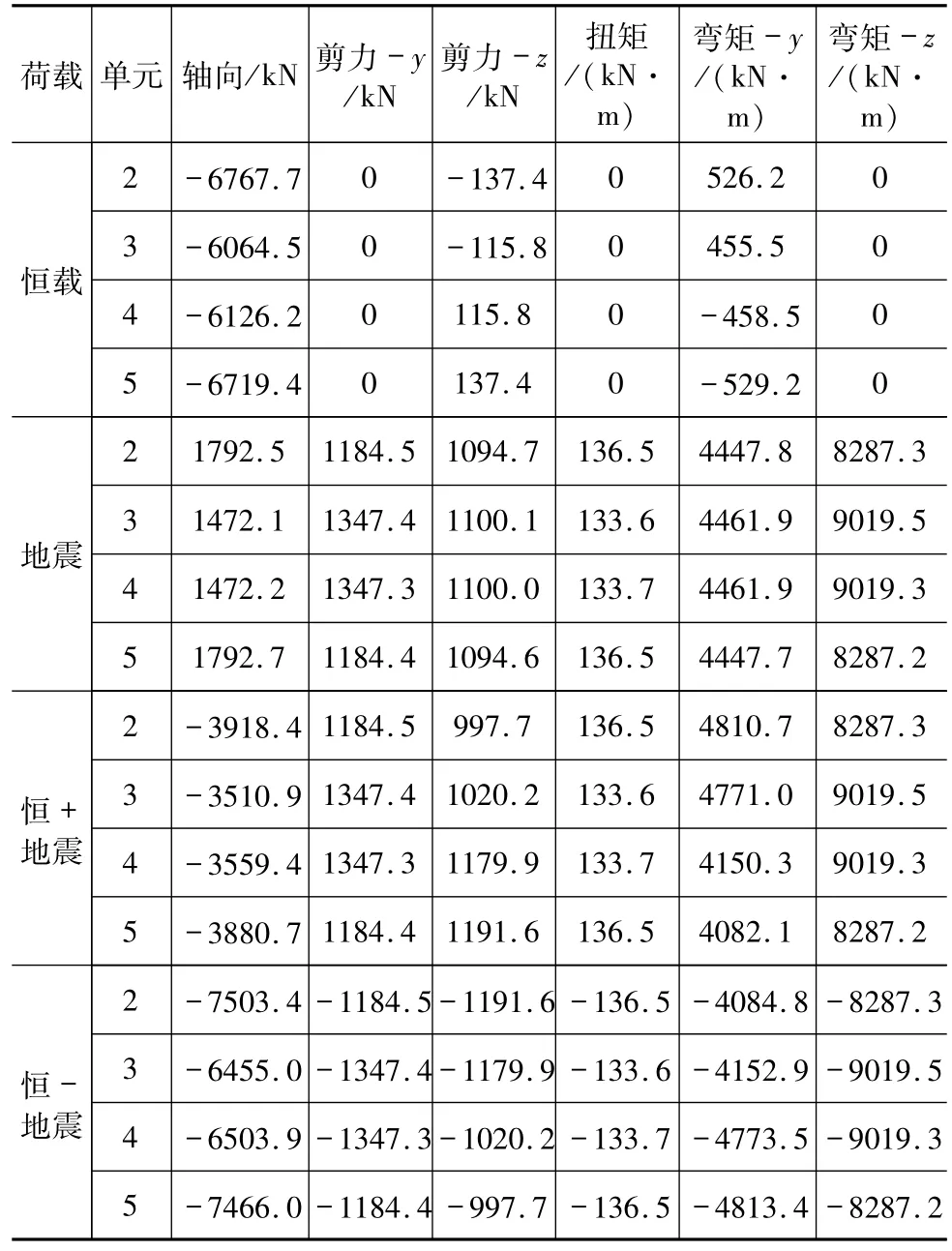
表2 E2地震作用下作用效应组合墩底内力

E2地震作用下，延性构件的有效截面抗弯刚度按下式计算，其余构件抗弯刚度仍按毛截面［4］：

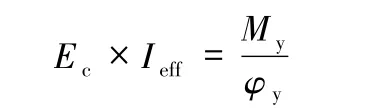
式中：Ec为桥墩的弹性模量(kN/m2)；Ieff为桥墩有效截面抗弯惯性矩(m4)；My为屈服弯矩(kN·N)；Φy为等效屈服曲率(1/m)。

E2地震作用下，桥墩单元强度验算有部分通不过，显然截面已经进入弹塑性，进行能力保护构件桥墩塑性铰区抗剪强度验算(考虑抗弯超强系数)，全部通过。墩顶顺桥向最大位移3.48 cm，横桥向最大位移0.24 cm，均满足容许位移［8］。

4.2 时程分析

选波：进行地震安全性评价的桥址，设计地震动时程应根据地震安全性评价的结果确定；未进行地震安全评价的桥址，可采用设计加速度反应谱为目标拟合加速度时程。正确输入地震加速度时程曲线，要满足地震动三要素，即频谱特性、有效峰值和持续时间。频谱特性要求所选波的特征周期与设计桥梁对应场地的特征周期相近；持续时间为5～10倍的结构基本周期；有效峰值则通过调幅来实现。

用程序自带的地震波数据生成器选择三条与该桥址特征周期Tg=0.4s相近的地震波(1940，El-Centro-Site，270-De、1952，Hollywood Storage P.E.，270 Deg、1985，Mexico City，Station 1，180 Deg)，为了与设计时的地震烈度相当，对选用的地震记录加速度时程曲线应按比例放大或缩小。设计加速度峰值PGA等于设计加速度反应谱最大值Smax除以放大系数2.25，即：

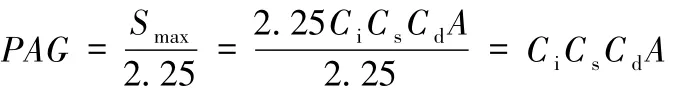
式中参数见《抗震细则》中公式5.2.2的说明。图6列出El-Centro Site三个方向地震波［10］。

4.3 反应谱和时程分析对比

地震作用下反应谱法和弹性时程法墩底最大内力对比见表3。对于y方向的剪力、扭矩、平面外弯矩均是反应谱法大于时程法。内力对比满足《抗震细则》6.5.3，在E1地震作用下，线性时程法的计算结果不应小于反应谱计算结果的80%。

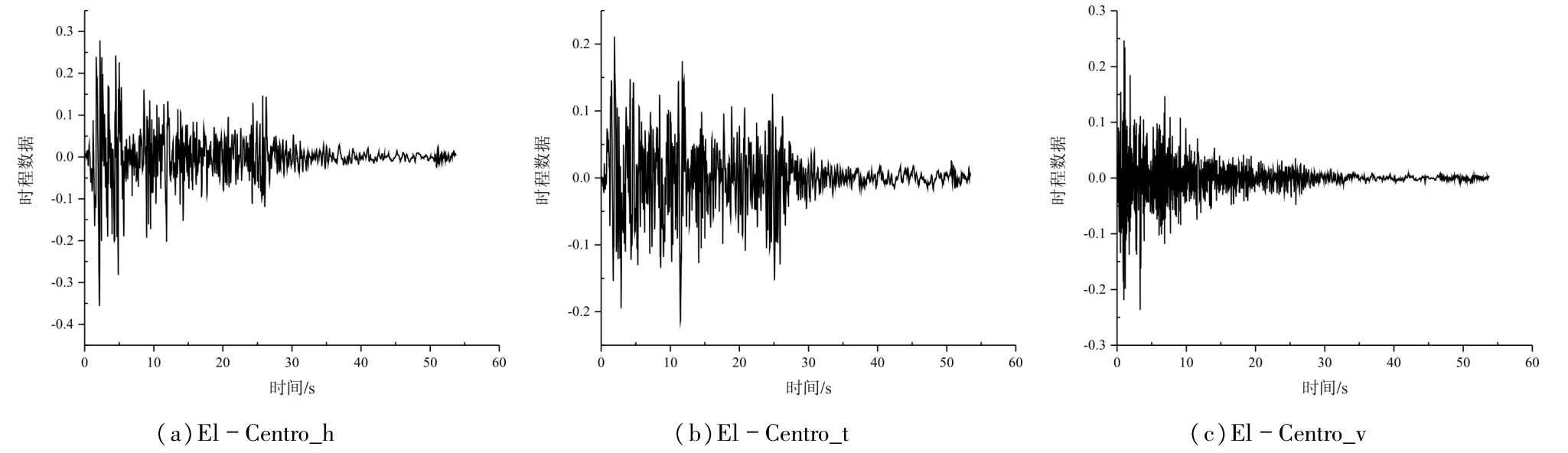
图6 El-Centro Site地震波

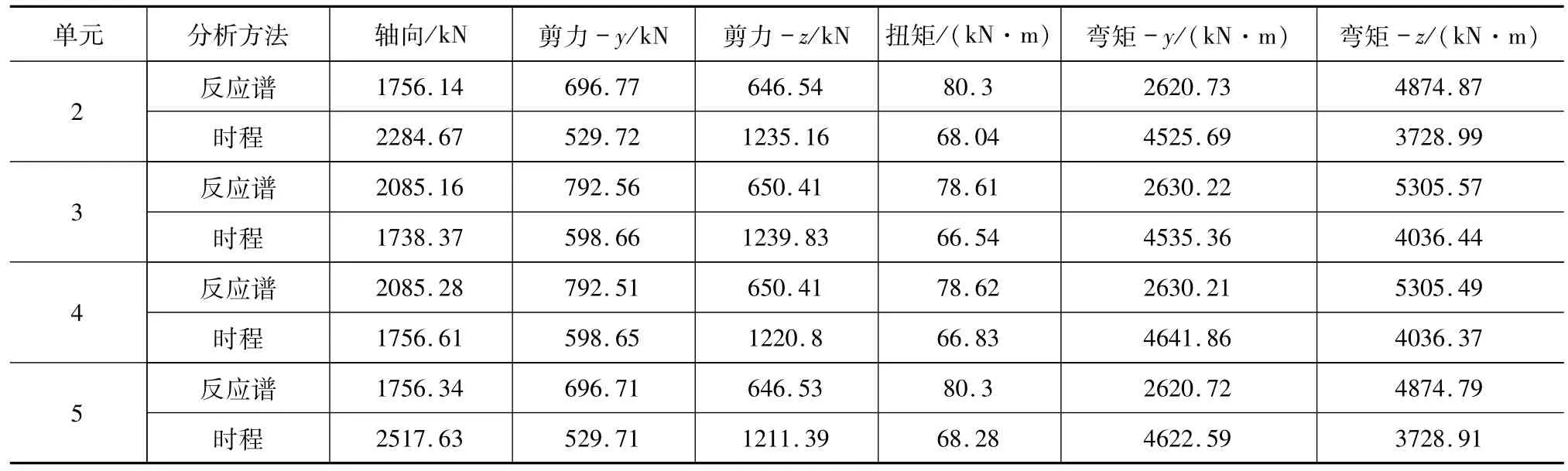
表3 两种分析方法墩底内力对比

5 结论

结构抗震设计常规方法是反应谱法和动态时程法，反应谱法将动力问题静力化，概念简单，计算方便，可以用较少的计算量获得结构的最大反应值。因此，世界各国规范都把它作为一种基本的分析手段。但是它也有很多缺陷，比如反应谱是弹性范围内的概念，当结构在强震下进入塑性工作阶段时不能直接用；另外，地震作用是一个时间过程，而反应谱只能得到最大反应，不能反映结构在地震动中的时间历程和地震动持时效应。多振型的反应谱法，由于反应谱仅能结构各振型反应最大值，不能反映其正负和时间，给振型组合造成混乱［9］。

时程分析法是对结构物的运动微分方程直接进行逐步积分求解的一种动力分析方法。由时程分析可得到各个质点随时间变化的位移、速度和加速度动力反应，进而计算构件内力和变形的时程变化。时程分析法作为反应谱法的一种补充，也就是说满足了规范要求的时候是可以不用它计算结构的。《抗震细则》规定时程分析的最终结果，当取3组时程波计算时，应取3组计算结果的最大值；当采用7组时程波计算时，可取7组计算结果的平均值。

本文针对三跨连续刚构借助Midas/Civil建模并用反应谱法进行E1、E2地震作用下的验算。在E1地震作用下，结构在弹性范围内工作，基本不损伤；在E2地震作用下延性构件(墩柱)进入了塑性，此时需要强度和位移双重验算，对于梁桥来说，如果是规则桥梁，需要满足位移条件即墩顶位移小于容许位移；如果是非规则桥梁，桥墩是矮墩(计算长度与矩形截面计算方向的尺寸比小于2.5)，须在组合作用下满足强度要求。如果不是矮墩，则需要对塑性铰转动能力进行验算。对于能力保护构件，包括盖梁、支座和基础以及墩柱塑性铰区域的斜截面抗剪强度验算。本桥在E1地震下结构处于弹性，满足强度要求，E2地震在桥墩进入了塑性，由于是规则桥梁，仅需要对桥墩墩顶位移验算。满足要求，对于能力保护构件桥墩塑性铰区域抗剪(考虑抗弯超强系数)也满足要求。本文同时用线性时程补充计算得出了结构关键单元内力、位移随时间变化曲线。

能力设计方法的基本概念是在结构体系中的延性构件和能力保护构件之间，确立适当的强度安全等级差异，确保结构不会发生脆性破坏，能在概率意义上最大限度防止结构倒塌破坏［5］。