基于小波阈值的动车组模型脉动压力提取方法研究

同晓雅，陈春俊，杨劼立，张 振

(西南交通大学机械工程学院，四川成都 610031)

0 引言

随着列车运行速度的不断提高，空气动力学效应加剧[1]，动车组表面空气脉动压力所产生的气动载荷会引起列车的结构振动甚至变形，影响乘客乘坐的舒适性，行车的安全性[2]。因此，研究动车组的表面脉动压力不仅可对气动噪声进行控制，而且对列车安全运行具有重要意义。目前，空气动力学的研究方法主要有在线实车试验、数值模拟、模型试验等[3]。由于脉动压力在实际线路易受复杂环境的影响，目前大多采用数值模拟的方法进行研究，王亚南和陈春俊[4]等人采用大涡模拟方法，研究高速列车表面脉动压力。本文利用动车组模型试验来进行表面脉动压力的提取不仅能为数值模拟提供验证依据，而且相比实际线路更易控制环境参数，能研究更多工况[5]。因此，本文利用动车组模型试验来进行表面压力的测试。相对于航空领域，高速列车领域对脉动压力的研究起步较晚，K. Nagakura[6]在风洞中对列车模型进行气动噪声分析和声源定位，指出高速列车气动噪声的主要根源为车体表面脉动压力。

对列车表面脉动压力的提取研究不仅能为列车的结构设计提供参考依据，还能为列车的减振降噪提供参考。基于此，本文设计出一个动车组模型表面压力测试系统，用于对表面压力的测试，并且基于传感器输出模型，利用小波阈值去噪消除表面压力的随机干扰，基于EMD利用相关系数得到了测点处的脉动压力值，最终预测气动噪声，为后续列车表面压力和降噪研究提供了支撑作用。

1 传感器输出模型

微压阻式压力传感器由于灵敏度高，体积小，对流场影响小，广泛应用于高速列车表面压力测试中，因此，动车组模型试验采用相同的传感器。其核心部分是一个硅膜片结构，当外界气压作用于薄膜时，薄膜受力变形，在薄膜边缘处应力集中，在此处通过扩散的方式生成4个半导体电阻，4个电阻构成一个惠斯登电桥[7]。在动车组模型测试中，当压力作用于薄膜时，压敏电阻由于其压阻效应电阻率发生变化，从而引起电阻阻值及电压输出值变化，通过力-电变换的敏感元件得到相应的输出压力，结合试验环境可分析微压阻式压力传感器输出压力如式(1)所示。

p(t)=p0(t)+pa(t)+qa(t)+n(t)+x(t)

(1)

式中：p(t)为传感器输出压力；p0(t)为平均压力；pa(t)为列车表面湍流所产生的脉动压力；qa(t)为振动引起的压力(以下简称振动压力)；n(t)为风机噪声引起的压力(以下简称噪声压力)；x(t)为电磁等随机干扰。

平均压力是在试验当地的大气压基础上变化，一般为kPa级，可通过滤波或者简单的数据处理获得，但是，在滤掉的成分里包括引起气动噪声的脉动压力、振动引起的压力、风机噪声引起的压力以及电磁等随机干扰，因此，本文拟运用小波变换阈值去噪方法消除电磁等随机干扰，根据相关系数分离出振动压力和噪声压力，最终提取出脉动压力。

2 数据处理及动车组模型试验

2.1 小波阈值去噪

实际的传感器测试信号总是受到噪声干扰，小波变换方法由于其独特的优势被广泛应用于噪声处理中，其分解层数和每层阈值都会影响去噪效果[8]。

本文通过计算小波分解后的每层尺度系数与原始信号的相关性来确定分解层数，相关性系数p越大表明相关性越强。

(2)

式中：x(n)为原始信号；ai(n)为小波分解后第i层的尺度系数。

由概率统计可知，白噪声信号的自相关函数如式(3)所示，其自相关函数在m=0时最大，然后迅速衰减至零，周期信号的自相关函数仍为周期信号，标准差为σ的零均值正态分布落在±3σ之外几乎为不可能事件。

(3)

因此在小波分解后，若小波分解的细节系数自相关函数呈现白噪声特性，认为绝对值大于3σ的细节系数是信号有用系数，则阈值T的选择区间为[-3σ,3σ]，σ为该层细节系数的标准差；若小波分解的细节系数自相关函数呈现周期信号特性，则阈值选择为T=0。小波变换去噪后，通过软阈值法对信号进行重构，也可看做小波分解的逆过程[9]。利用上述小波变换阈值去噪方法来消除传感器的电磁等随机干扰。

2.2 脉动压力提取

经验模态分解(EMD)可以避免傅里叶变换产生的许多事实上不存在的高、低频成分，同时，与小波变换相比，没有小波基的选择问题，该方法得到了广泛使用[10]。

经验模态分解基于信号自身的特征使真实存在的不同尺度波动或趋势逐级分解开来，产生一系列固有模态函数(IMF)，原始数据序列x(t)可由这些IMF分量cj(t)以及一个均值或趋势rn(t)表示，如式(4)所示。

(4)

其中，第一个IMF分量 代表原始数据序列中最高频的组成成分，以此类推，IMF分量c2(t)、c3(t)分别代表原始数据序列中频率由高到低的组成成分。

对去除随机干扰的信号和振动信号以及风机声压值进行EMD分解，将分解的每对IMF分量根据式(5)做相关性分析，得到每对IMF分量的相关性系数。根据表1所示的相关程度表[11]，可判断出相关系数大于0.4的IMF分量重构的压力即为振动压力和风机噪声压力，则重构剩余分量即为脉动压力。

(5)

表1 相关程度表

2.3 动车组模型试验传感器测点位置

动车组模型表面压力测试试验系统包括基本的硬件和软件设计。硬件设备主要是由动车组模型、传感器、计算机、数据采集卡、变频器、三相交流异步电机、离心通风机、有机玻璃风道以及采集器等组成，软件设计主要包括风速闭环控制系统设计和数据采集软件的应用。其压力传感器、传声器、振动传感器测点如图1所示。

(a)压力传感器

(b)传声器

(c)振动传感器

分别测量在不同风速下的动车组模型表面压力、噪声以及振动数据，选取前车车头位置处的压力测点进行脉动压力的研究。

3 脉动压力提取

3.1 小波阈值去噪

如图2所示为车头位置处的动车组模型表面压力。通过2.1节的方法利用db3小波对表面压力的随机干扰进行降噪。首先确定小波分解层数，图3为小波分解后每层尺度系数与原始信号的相关性，相关性随着分解层数的增大而减小，当分解层数为8层后，不仅本层相关系数小，而且后续层数的变化不大，因此，选取小波变换的分解层数为8层。

图2 表面压力

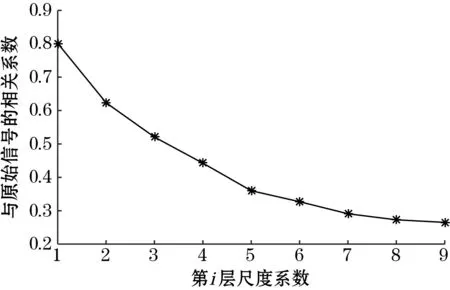
图3 尺度系数的相关系数

对图2所示的原始表面压力进行8层小波分解，小波分解后的每层细节系数的自相关函数如图4所示。

图4 细节系数的自相关函数

由图4可知，d1～d4呈现白噪声自相关函数特性，则阈值选择为T=3σ；d5～d8呈现周期信号自相关函数特性，则阈值选择为T=0。因此，确定小波分解的各层阈值为T={0.013，0.017，0.030，0.042，0，0，0，0}。利用各层阈值去噪后，重构尺度系数和细节系数，得到消噪后的表面压力，如图5所示，可以看出，小波阈值去噪消除了表面压力的随机干扰。对降低随机干扰的表面压力进行滤波，得到脉动压力、振动压力和风机噪声压力(以下简称为原始压力)。

图5 去噪压力

3.2 提取脉动压力

通过2.2节的方法提取出脉动压力。对振动和原始压力数据进行EMD分解，都分解为11层，将分解的每对IMF分量根据式(5)做相关性分析，得到每对IMF分量的相关性系数，相关系数如表2所示，相关系数大于0.4的IMF分量共有3个，为IMF9、IMF10和IMF11。

表2 振动IMF分量的相关系数

同样对风机声压值和去除振动压力的信号进行EMD分解，分解为11层，得到每对IMF分量的相关性系数如表3所示，相关系数大于0.4的IMF分量共有4个，为IMF4、IMF8、IMF10和IMF11。则重构剩余分量即为提取的脉动压力，如图6所示。

表3 风机噪声IMF分量的相关系数

图6 脉动压力

4 结果分析

参照声压级的定义,脉动压力级[12]可以定义为

(6)

式中：p0为基准声压，p0=2×10-5Pa;p为测点处脉动压力值。

(7)

式中：N为数据的长度；Apfl(i)为气动噪声；Mpfl(i)为传声器所测的噪声(混合噪声)。

利用FFT将时域信号转换到频域，提取出的脉动压力信号所预测的气动噪声为图7所示的实线，传声器所测的噪声(以下简称混合噪声)为图7所示的虚线。由图7可知，传声器所测的噪声比提取出的脉动压力信号所预测的气动噪声大，主要是因为传声器所测噪声不仅包括气动噪声，而且有风机运行的机械噪声等，导致气动噪声小于传声器所测的噪声。根据式(7)可计算出气动噪声与混合噪声的相关性为0.716 8，根据表1所示的相关程度表可知两者具有强相关性，这与试验环境所一致。同时气动噪声和混合噪声的变化趋势基本一致，转折频率都为120 Hz，在转折频率前气动噪声和混合噪声都有先减小再增加的趋势，验证了上述脉动压力提取方法的正确性。

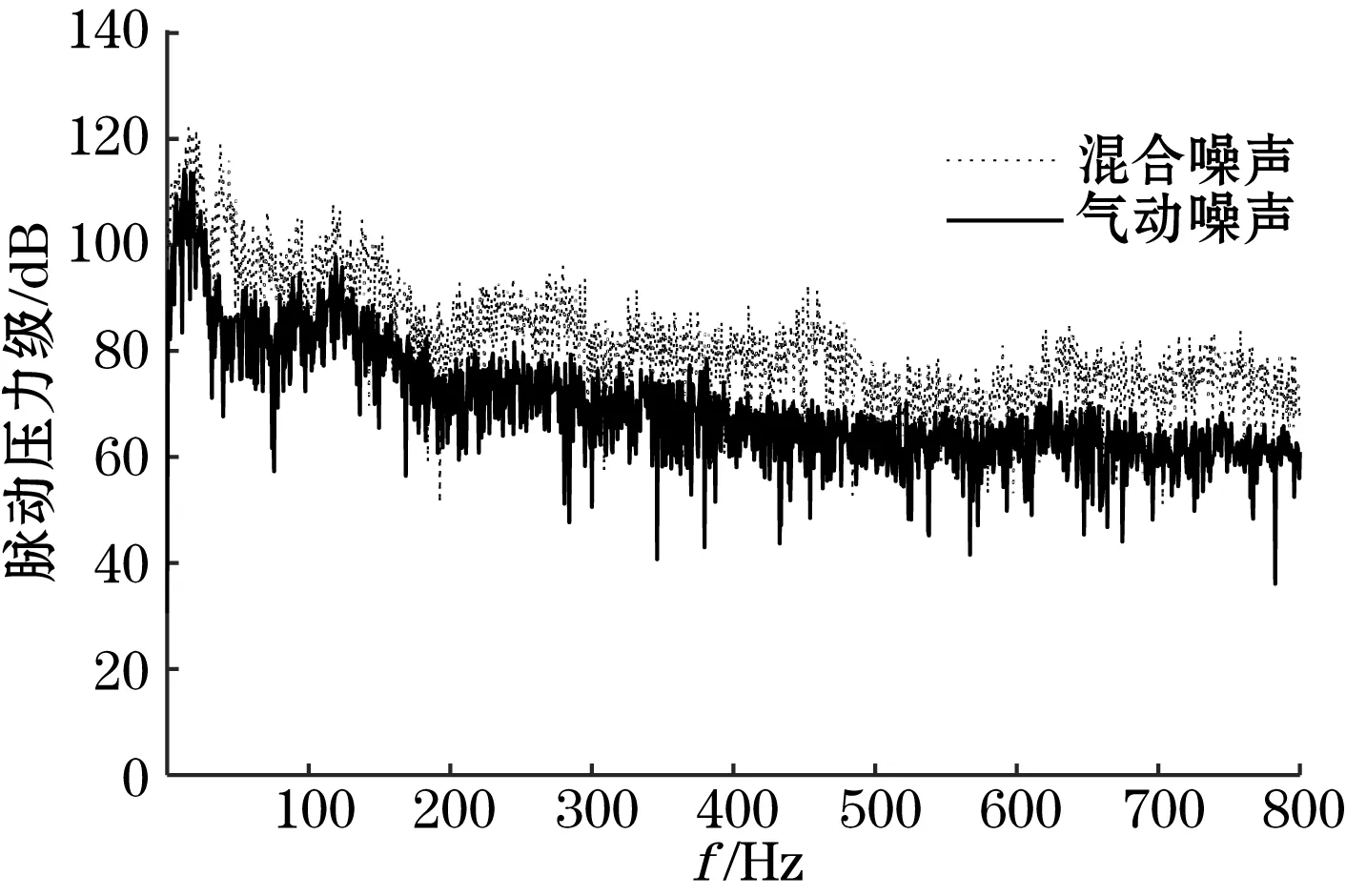
图7 脉动压力级

由图7可知，气动噪声的频带较宽，低频幅值比高频大，有先减小再增加再减小的趋势。利用脉动压力可对动车组表面气动噪声进行预测，从而可对气动噪声进行针对性控制，不仅可优化列车的结构，同时可减小对乘客和沿线居民的影响，对列车减振降噪提供参考。

5 结束语

通过对动车组模型进行表面压力、振动以及噪声的测试试验，并对数据进行去噪处理和脉动压力的提取，得到以下结论：

(1)完成压力、振动和噪声传感器的测点布置，测量出相应值，结合所使用的的传感器以及试验环境分析出压力输出模型，利用小波阈值去噪对表面压力进行降噪，利用尺度系数与原始信号的相关性来确定分解层数，根据3σ准则进行细节系数的阈值选取，该方法可对随机干扰进行有效的消除，根据相关系数分离出振动压力和噪声压力，最终提取出脉动压力；

(2)对提取出的脉动压力所预测的气动噪声和传声器所测的混合噪声做频谱分析，气动噪声和混合噪声的变化趋势基本一致，相关性为0.716 8，气动噪声和混合噪声的转折频率都为120 Hz，