压阻式压力传感器灵敏度的仿真方法

2019-03-28杨娇燕林立娜李奇思熊继军

仪表技术与传感器 2019年2期

杨娇燕，梁庭，李鑫，林立娜，李奇思，赵丹，雷程，熊继军

(中北大学,仪器科学与动态测试教育部重点实验室,动态测试技术山西省重点实验室,山西太原 030051)

0 引言

硅压力传感器广泛应用于汽车工业、生物医学、工业控制、能源化工等领域[1]。尽管压力传感器技术已经相对成熟，但不同的应用领域对压力传感器有不同的要求，硅压力传感器因其低廉的成本[2]，微小的结构仍是重点研究对象。

硅压阻式压力传感器由弹性敏感元件和转换元件组成[3]，弹性平膜片作为压力敏感元件，4个构成惠斯登电桥的扩散电阻作为转换元件，将膜片上的应力变化转换为电信号输出。弹性敏感膜片常采用方膜和圆膜，同样大小的方膜有更大的应力更高的灵敏度并且工艺制备更简便，因此本文采用方形膜作为敏感膜。传感器的灵敏度主要由敏感膜上的应力分布决定[4]。敏感膜的应力分布问题可以等效成薄板问题，但是方形薄板的小变形很复杂，难以精确的计算出薄板上每一点的应力，利用有限差分法可以近似计算出薄板的最大变形和最大应力值。但是压敏电阻上每一点的应力都不同，用这种数值分析方法计算出的传感器输出电压、灵敏度和实际值有较大的偏差。利用有限元仿真软件可以得到敏感膜片上任一点的应力大小。压敏电阻采用离子注入或扩散工艺制作，压敏电阻比较薄且厚度也不能精确控制，在仿真建模时对压敏电阻厚度方向的设置并不能提高仿真精度，因此在进行仿真建模时忽略压敏电阻的厚度。用Ansys有限元仿真软件对敏感薄膜进行受力分析得到敏感薄膜上的应力分布，通过定义路径得到压敏电阻所在位置的应力大小，对压敏电阻所在路径的应力积分然后除以压敏电阻的长度求得压敏电阻所在位置的应力平均值，乘上压阻系数，计算出压敏电阻的变化从而求得输出电压。

本文设计了2种不同的传感器仿真模型并运用积分算法对其进行仿真分析，将仿真结果和实际值对比，验证了积分算法的可靠性，同时得到了更精确的仿真模型。对今后传感器的设计提供了一种简洁而有效的仿真方法。这种方法充分利用Ansys有限元仿真软件对传感器敏感膜片的应力分析及其结果后处理功能，得到传感器在不同压力下的输出电压，计算出灵敏度，以指导不同应用需求的压力传感器的设计与制造。

1 工作原理

压阻式压力传感器是基于硅的压阻效应制备的。半导体材料受外力作用时，晶格变形导致载流子迁移率变化，引起材料电阻率ρ变化[5]，表示为

(1)

式中：ρ为电阻率；π为压阻系数；σ为应力。

半导体材料的压阻系数具有方向性，其电阻率在不同晶向下不同。建立正交直角坐标系，当晶轴与坐标轴同向分布时，其电阻变化率由纵向l，横向t，垂向s上的压阻效应之和表示为

(2)

式中垂向应力σs相比纵向应力σl和横向应力σt可忽略不计。

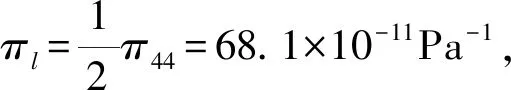
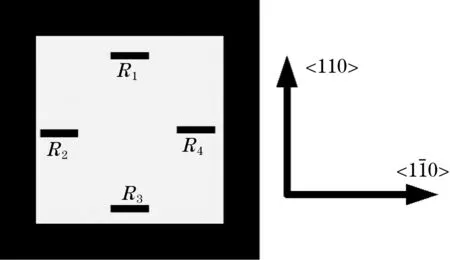
图1 传感器结构示意图

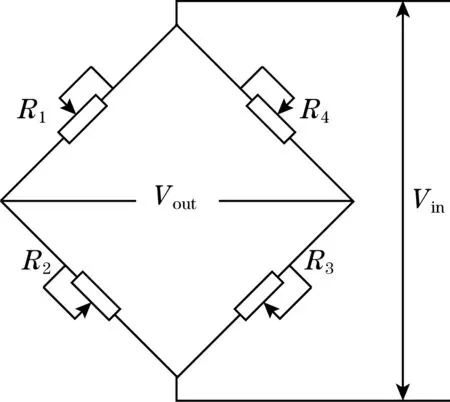
图2 传感器电路原理图

当无压力作用于敏感膜片时，4个电阻的阻值完全相同R1=R2=R3=R4=R，电桥输出电压为0；当有压力作用时4个电阻发生不对称变化，电桥输出电压。

(3)

沿相同晶向排列的压敏电阻变化相等，ΔR1=ΔR3=ΔR′，ΔR2=ΔR4=ΔR″。电压输出公式简化为

(4)

传统的中心点算法用压敏电阻中心点位置的应力代替整个压敏电阻上的应力，计算简单方便，但结果误差较大。为了精确的计算压敏电阻的变化量，需要对压敏电阻整个长度上的变化量积分求平均，即

(5)

式中：l为压敏电阻长度；L为敏感膜片边长。

图3中压敏电阻长度方向为x轴，宽度方向为y轴，σx，σy为压敏电阻上沿坐标轴方向的应力。压敏电阻的宽度和长度相比较，宽度很小，所以认为横向应力σl和纵向应力σt只在x方向上变化不在y方向上变化。

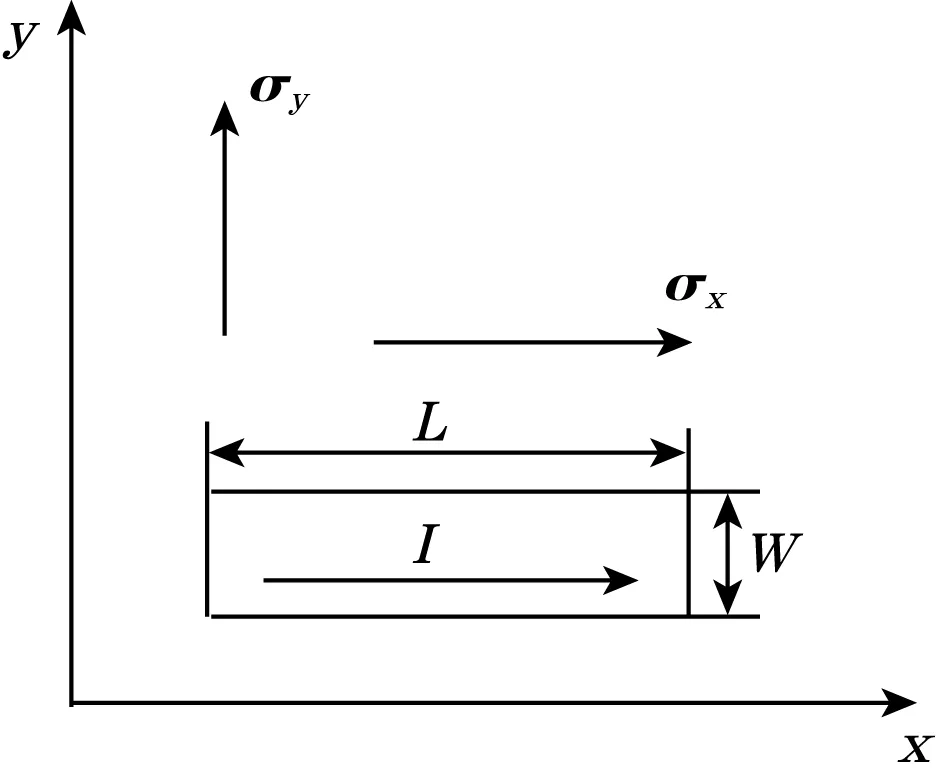
图3 压敏电阻的位置

将坐标位置代入式(5)得：

(6)

式中：x1为压敏电阻起始位置的坐标；x2为压敏电阻终点位置的坐标。

当压敏电阻平行于膜片边缘排布时σl=σx,σt=σy；

(7)

式中A为平行于膜片边缘放置的压敏电阻上的平均应力。

(8)

当压敏电阻垂直于膜片边缘放置时σl=σy,σt=σx；

(9)

式中B为垂直于膜片边缘放置的压敏电阻上的平均应力。

(10)

将式(8)、式(10)代入式(4)传感器的输出电压表示为

(11)

传感器的灵敏度是指单位压力下传感器的输出电压[9]。根据不同压力(Pin)下的输出电压，做出输出电压(Vout)随外界压力变化的曲线，做线性拟合求其斜率，即为传感器的灵敏度S。

(12)

2 仿真分析

本文研究的敏感膜片由设计要求和工艺条件确定为1 mm×1 mm×60 μm，芯片尺寸为3.2 mm×3.2 mm×1 mm。有限元分析软件Ansys仿真分析得到敏感膜片表面的应力差分布，为了得到精确的仿真结果，对压敏电阻所在位置进行路径定义。

主要的仿真步骤包括创建几何体模型，添加模型材料属性(单晶硅的杨氏模量为170 GPa，泊松比为0.3[6])，划分网格，施加载荷与约束，路径操作，数据处理。在对传感器芯片建模时，通常采用四边固支的方形，固定支持加在方形的四周，认为敏感芯片四周的支撑是完全刚性的，在受压时四周不发生形变，所有的变形集中在敏感膜片上。由于方形敏感膜片的应力分布是完全对称的，建模时只需建立敏感膜片的1/4模型，图4为四边固支的方形模型(模型1)。当敏感膜片受到压力时，膜片表面的应力分布如图5所示，从膜片边缘到中间应力差逐渐减小，在膜片边缘中心点处应力差最大。为获得最大的灵敏度，压敏电阻应放置在膜片的边缘处。但由于光刻和深硅刻蚀等实际工艺的限制[9]，压敏电阻布置于膜片四边中点靠内40 μm处。沿压敏电阻所在位置定义积分路径，图6为积分路径，在满量程载荷(2 MPa)下，与膜片边缘平行放置的压敏电阻所在位置的平均应力为83.926 MPa/μm，电阻变化量为77.112 Ω。与膜片边缘垂直放置的压敏电阻所在位置的平均应力为-58.837 MPa/μm ，电阻变化量为-54.026 Ω，负号表示电阻减小，根据式(10)计算得到满量程输出电压为254.012 mV。利用同样的方法得到不同压力下的输出电压，图7为加载压力和输出电压的曲线图，线性拟合得到传感器的灵敏度为0.123 mV/kPa。

图4 四边固支的方形膜模型

图5 四边固支时膜片表面应力分布

图6 方形模型的积分路径

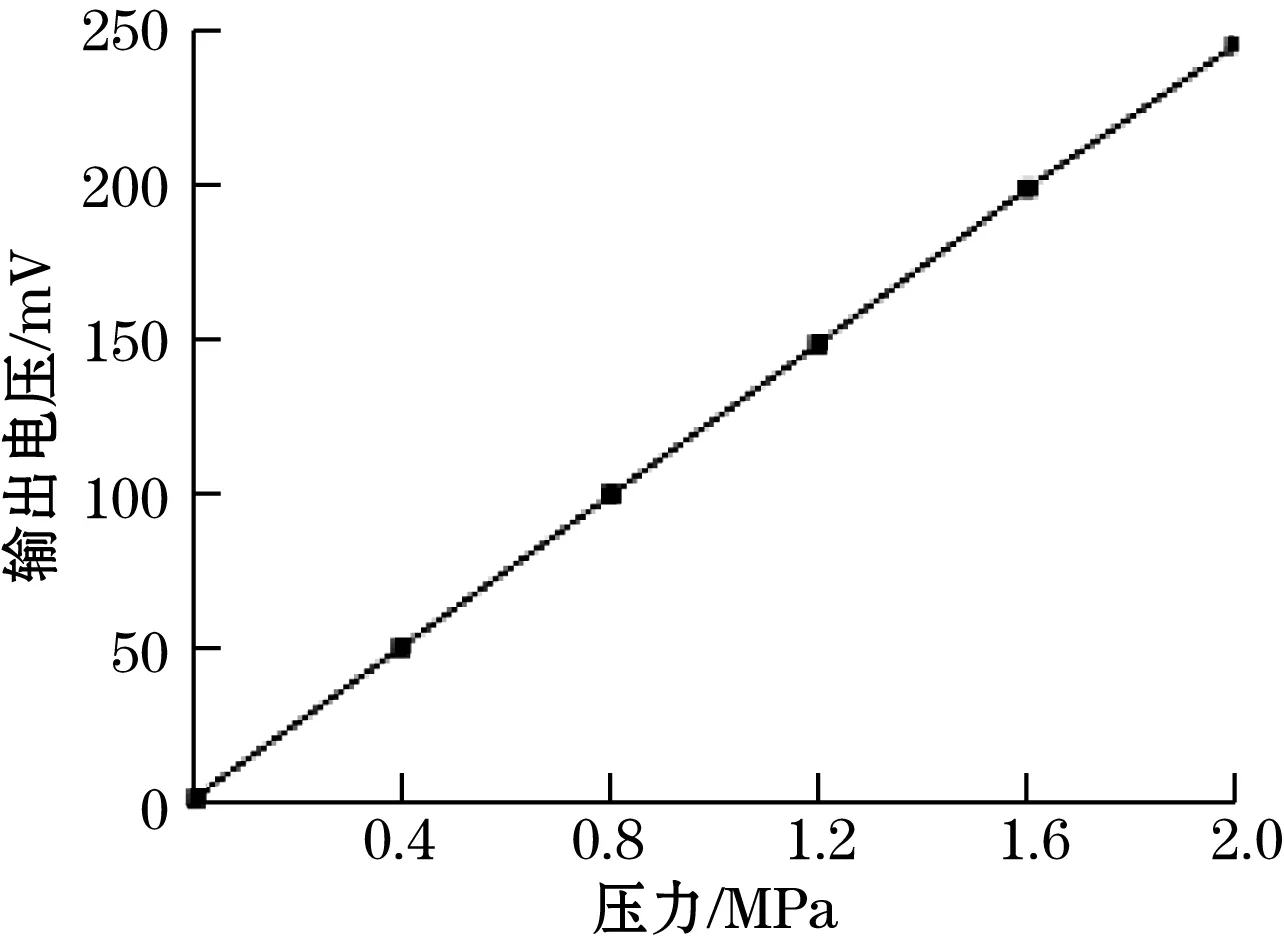
图7 四边固支模型不同压力下的输出电压

当仿真模型按照传感器芯片的实际结构建立时，仿真模型如图8所示。图8为C型结构(模型2)，固定支撑加在硅玻璃接触的下底面。网格划分大小和模型1相同，仿真分析得出方形膜表面的应力差分布如图9所示。通过定义路径(如图10所示)，结果后处理，得到满量程压力下，与敏感膜片平行放置的平均应力为72.711 MPa，电阻变化量为66.774 Ω；与膜片边缘垂直放置的压敏电阻所在位置的平均应力为-48.913 MPa，电阻变化量为-44.917 Ω，根据式(10)计算得到满量程输出电压为208.236 mV。输出电压和加载压力的关系曲线如图11所示，传感器的灵敏度为0.104 mV/kPa。

图8 底面固支的C型模型

图9 C型模型敏感膜片表面的应力分布

图10 C型结构的积分路径

图11 C型模型不同压力下的输出电压

3 芯片制作

本文研究的传感器选用(100)晶向，400 μm厚的双抛绝缘体上硅(SOI)，通过离子注入对SOI掺杂，深硅刻蚀工艺刻蚀出压敏电阻；沉积一层氧化硅做保护层，反应离子刻蚀开电极孔，电极孔重掺杂形成欧姆接触区。磁控溅射鈦铂金制作金属引线，在525 ℃下退火形成欧姆接触。深硅刻蚀出敏感薄膜，硅玻璃键合形成绝压参考腔。制作完成的压力传感器芯片正面结构如图12所示。

图12 传感器芯片正面结构

4 传感器测试与分析

在完成的压力传感器芯片中随机的选取芯片，采用引线键合的方式将传感器芯片封装在不锈钢基座上。对完成封装的传感器进行加压测试，测试平台主要包括直流供电电源，高精度万用表，台式气压泵。将压力传感器安装在台式气压泵上，从常压开始加压每次增加0.1 MPa直到2 MPa，记录每个压力下传感器的输出电压值，输出电压随外界压力的增大而增大。测试结果如图13所示，传感器的灵敏度为0.102 5 mV/kPa。

图13 不同压力下输出电压

将传感器的测试结果和2种模型下的仿真分析结果比较，传感器的实际灵敏度和模型1的仿真结果相对误差为19.72%，和模型2的仿真结果的相对误差为1.76%，模型2的结果更准确，其微小的误差可能来自实际制作过程中不可避免的工艺误差，例如光刻的精度对敏感膜片的尺寸，压敏电阻的大小的影响，深硅刻蚀的均匀性造成了敏感膜片厚度的误差。利用模型2可以精确计算传感器的输出电压及灵敏度。

模型1的仿真结果和实际测试值的相对误差较大。主要是由模型1和实际传感器模型偏差较大造成的。当压力作用于敏感芯片时整个芯片受力，模型1将敏感膜片作为芯片的唯一受力部分，忽略了压力传感器芯片除敏感膜片之外的部分受压变形，造成了仿真结果和实际测试结果有较大偏差。