弹道导弹群目标多普勒速度估计算法

靳俊峰，曾 怡，廖圣龙

（中国电子科技集团公司第三十八研究所孔径阵列与空间探测安徽省重点实验室，合肥230088）

0 引 言

为了提高突防能力，弹道导弹在飞行中段经常会采用投放干扰箔条和模拟弹头的假目标，或将末级火箭炸成碎片形成干扰碎片云等突防措施。由于在飞行中段没有大气阻力，弹头、诱饵、整流罩、母舱、碎片残骸等均在弹道附近伴随着弹头高速运动，在空间形成扩散范围达几千米、相互靠近的群目标［1］。

雷达在对导弹群目标进行多普勒测速时，由于群内目标密集度高、位置变化随机性强、相互遮挡严重，无法对群内目标单独进行测速，会发生多普勒速度大幅跳动情况，严重影响目标测距精度，导致在目标关联过程中经常出现混批、错批，给后续的目标识别、轨道外推等带来很大难度，严重时甚至会丢失目标。如何解决群目标多普勒速度估计是实现群内目标正确关联的核心问题［2］。

在航天测控领域中，一般采用多测速系统实现外空间飞行器的高精度测速，且仅限于合作的单目标。但是，在弹道导弹预警系统中，雷达面对的是饱和攻击，弹头、诱饵、干扰、配重等会形成群目标，直接进行多普勒测速会由于密集目标遮挡等原因测速不准，此外测量的速度也无法与群目标进行一一对应，增大了航迹跟踪难度。

本文提出了一种新的弹道导弹群目标多普勒速度估计算法。首先将量测多普勒距离补偿去掉，这样群目标在多帧之间可保持距离量测的一致性，不会由于多普勒速度测量的跳动导致群目标多帧之间相关错误，然后采用最优分配策略进行群目标关联［3］，并采用基于弹道导弹动力学的UKF滤波算法进行目标位置、速度估计，最后根据滤波结果进行多普勒速度重新估计，目标距离经多普勒重新补偿后进行上报。

1 多普勒补偿

弹道导弹相对雷达高速运动时，由于传播路程差的原因，跟踪过程中会出现跨距离单元、跨多普勒单元现象，使雷达系统常用的相参积累处理失效。必须通过对目标回波信号进行速度、加速度补偿才能实现有效的积累［4］。

假设目标相对雷达多普勒速度为Vr，向站运动时多普勒速度为正，背向雷达运动时多普勒速度为负，雷达带宽为Bw，发射脉冲宽度为Pw，工作频点为Fr，则目标多普勒补偿距离为

在群目标跟踪过程中，由于群内目标互相遮挡，雷达无法直接测量群中每批目标的多普勒速度，而只能通过测量群目标回波中的峰值作为群目标多普勒速度。事实上群内目标速度是有差别的。显然，通过直接测量群目标多普勒速度进行距离补偿引入了人为误差，会导致后续相关、滤波出现错误。因此，需要对群目标量测距离进行去多普勒补偿。假设时刻t某量测距离为R（t），则去多普勒补偿距离为

雷达处理多普勒补偿时可以取脉冲前沿或后沿，此时多普勒补偿正负方向会相反，只需要在上面公式中改变正负号即可。后续的相关、滤波处理均使用去多普勒补偿距离。

2 基于综合多因子关联矩阵的最优分配算法

2.1 关联矩阵

关联矩阵是表示两个实体之间相似性程度的度量，对每一个“量测⁃航迹”对都必须计算其关联矩阵。关联概率大小取决于特征向量的隶属度和权向量，通过归一化模糊评判向量和权向量构成综合隶属度评判函数［5］，航迹i与量测j的目标关联概率为

关联概率dij若小于阈值Pth，则认为航迹i与量测j无法关联，在关联矩阵中取值为0；若大于Pth，则可用于构建基于综合隶属度函数的关联矩阵IM：

其中，n表示航迹数，m表示量测数。

2.2 最优分配

弹道目标关联问题采用综合隶属度函数表示为关联矩阵后，对时刻k所有的量测与航迹关联的核心就是如何对关联矩阵进行分配。该分配问题可描述如下：

给定关联矩阵IM，对矩阵中的每个元素aij，找到一个分配X＝｛xij｝，使得总的隶属度Subjection＝最小化，同时满足以下限制：（1）任一量测j最多仅与一个航迹i关联，即＝1∀i；

（2）一个航迹i最多仅与一个量测j关联，即＝1∀j。

在分配算法中，允许xij为0或者1。如果量测数少于航迹数，则会出现有些航迹无法分配到量测，会出现量测无法关联到航迹。

对分配问题采用一种最优分配算法解决，步骤如下：

（1）首先对关联矩阵IM采用聚类算法进行分簇，满足簇内的量测与航迹综合隶属度大于0，而簇间的量测与航迹综合隶属度为0。通过分簇可将规模较大的分配问题转换为规模较小的分配问题，减少计算量；

（2）对关联矩阵IM每一行，找出最小的元素rowmin，并将该行中的所有元素减去该值；

（3）对关联矩阵IM每一列，找出最小的元素colmin，并将该列中的所有元素减去该值；

（4）比较矩阵行数n和列数m，不妨假设行数n小于列数m，统计最少需要多少直线来覆盖结果矩阵中出现的所有零值，如果此时的零值个数与n相同，找到最优分配，矩阵计算结束，否则转第5步；

（5）找出第4步中未被直线覆盖的最小非零值a，所有未被覆盖的元素减去a，对于被两条直线交叉覆盖的非零元素加a，重复第4步。

采用最优分配算法可以完成群内密集目标量测与航迹的准确配对。这是后续滤波、多普勒速度估计的基础。

3 弹道导弹动力学模型

根据弹道导弹从发射点到目标点的运动过程中的受力情况，可将其弹道分为3段。首先，根据导弹在飞行中发动机和控制系统工作与否，可将其弹道分为动力飞行段（简称主动段）和无动力飞行段（简称被动段）两部分。其次，在被动段则又根据弹头所受空气动力的大小分为自由飞行段（简称自由段）和再入大气层飞行段（简称再入段）两部分［6⁃7］。 表1给出了弹道飞行模型各段的飞行阶段及其受力情况。

表1 弹道导弹飞行阶段及其受力情况

3.1 主动段弹道目标运动模型

在地心地固坐标系ECEF下，设目标位置向量为p＝［px，py，pz］′，速度向量v＝［vx，vy，vz］′。 通过上述分析，可以建立弹道目标主动段的方程。

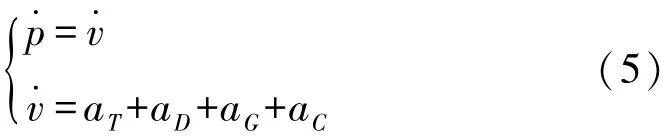
弹道目标主动段上的加速度主要分为4项：aT推进力产生的加速度，aD空气阻力产生的加速度，aG地心引力产生的加速度，aC外在力（科氏力和离心力）产生的加速度。

3.2 自由段弹道目标运动模型

自由段上的加速度的包括aG地心引力产生的加速度、aC外在力（科氏力和离心力）产生的加速度，可以得到自由段的运动方程：

3.3 再入段弹道目标运动模型

再入段上的加速度包括aD空气阻力产生的加速度、aG地心引力产生的加速度、aC外在力（科氏力和离心力）产生的加速度，可以得到再入段的运动方程：

4 群目标多普勒速度估计

根据弹道导弹动力学模型，采用UKF滤波算法可以得到目标精确的速度、加速度估计。假设某批目标站心坐标系下的时刻t滤波结果为X（t）、Y（t）、Z（t）、Vx（t）、Vy（t）、Vz（t），则可以得到该时刻的滤波多普勒速度为

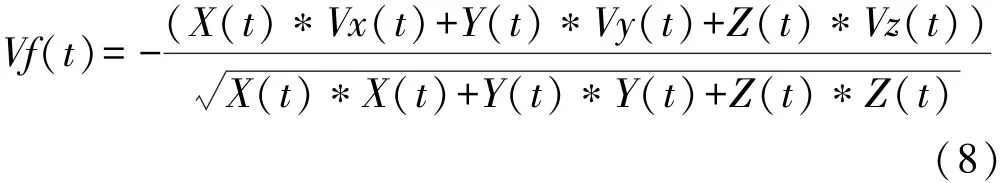
目标上报时可根据重新估计的多普勒速度进行距离补偿。该结果对群目标来讲明显好于脉冲多普勒测速直接补偿结果。

主要处理步骤：

（1）判断弹道导弹量测是否为群目标，如果是则对群目标量测距离进行去多普勒补偿，否则采用PD测速方式对单目标进行测速；

（2）对群目标建立量测⁃航迹关联矩阵，关联矩阵通过综合隶属度方法进行计算，并采用最优分配算法进行配对分配；

（3）对配对好的量测⁃航迹采用基于弹道导弹动力学的UKF滤波方法进行滤波，估计目标在站心系中的位置和速度；

（4）根据目标位置和速度计算多普勒速度，并在目标上报时根据该速度进行重新多普勒补偿。

弹道导弹群目标多普勒速度估计处理流程如图1所示。

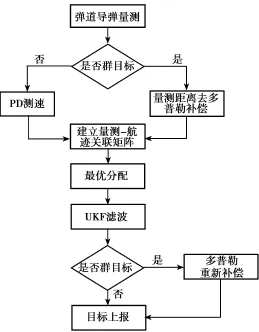
图1 弹道导弹群目标多普勒速度估计流程

5 算法分析

为了更真实仿真群目标过程，本文假设有7发导弹集火射击，仿真产生的飞行轨迹数据加入量测噪声。假设雷达工作频段为P波段，工作频点575 MHz，信号带宽2 MHz，对RCS为1 m2目标作用距离1 000 km，距离测量精度为50 m，方位角量测精度为0.2°，仰角量测精度为 0.2°，跟踪数据率为2 Hz。

弹道导弹飞行射程为600 km，飞行时间为520 s，飞行最大高度为215 km，雷达站位置距发射点距离为353.84 km。在弹道导弹飞行过程中生成了弹头群和弹体群目标，其中弹头群中包含7个目标，弹体群包含7个目标。

图2表示直接采用脉冲多普勒速度补偿距离进行目标跟踪结果。跟踪过程中发生了多次混批，且跟踪质量较差，起伏较大，不能够满足后续目标识别、弹道计算要求。

图3为采用本文算法跟踪结果。可见，去掉多普勒补偿后，由于目标在帧间能够保持一致性，有助于量测和航迹间的最优分配，经滤波后重新估计多普勒速度输出，可看出目标跟踪连续，相关正确率也大幅提高。

图2基于量测多普勒的群目标跟踪

图3 基于估计多普勒的群目标跟踪

6 结束语

弹道导弹群目标跟踪是构建防空反导体系的重要组成部分，也是完善战略预警体系的一个重要环节。针对弹道导弹群目标多普勒速度量测精度差、前后帧不一致问题，本文通过对大量实测数据事后分析及实测验证，提出了4步法弹道导弹群目标多普勒估计算法，即去多普勒补偿、最优分配、滤波估计、重新多普勒补偿。算法分析中设计了7发弹道导弹的复杂场景。结果表明，本文算法能够对弹道导弹群目标多普勒速度进行准确估计，相比直接测量多普勒速度有极大提高，特别在集火攻击等极端复杂情况下仍然能够给出准确速度估计。