全机落震载荷识别方法研究

侯乔乔

（中国飞机强度研究所，陕西 西安 710065）

落震载荷识别是指根据飞机着舰时机体响应来反演直接或者间接载荷。除航空领域以外，动载荷识别在航天、汽车、轨道交通、建筑桥梁等领域有着广泛的研究与应用，目的是为了有针对性地对结构的力学特性进行设计优化。

结构动力学第二类逆问题的研究始于上世纪70年代末，美国学者Bartlet F.D和Flannelly W.D[1]等为了研究直升机桨毂振动传递到主轴的载荷，通过测量加速度响应及系统传递矩阵计算了直升机主轴所受的外载荷。Hillary和Ewins[2]以应变测量为基础采用频域方法研究了悬臂梁结构的点激励载荷识别问题。Okubo N Tanabe S[3]采用频响函数求逆法研究了机床刀具切削力、汽车发动机的激振力识别问题。John O C[4]等人研究了载荷位置的识别问题，在对载荷位置做出假设的前提下取得了较好的结果。

在国内，南京航空航天大学姜金辉[5]等对分布随机动载荷的识别理论和方法做了系统的研究，对现有的频域法与时域法所涉及的方法进行了详细的研究对比。张方[6]等学者研究了结构连续分布的动态随机载荷识别技术，即基于广义正交多项式特征技术动态随机载荷识别模型，解决了在一定精度范围内通过有限测量部位来识别连续分布包含无限信息的随机载荷识别问题。

全机落震载荷识别的本质是反卷积求解问题，其难点是，载荷分布为三维的体分布，从国内外的研究来看，还没有形成对三维体分布载荷识别的成熟理论与方法，普遍应用的频域响应函数求逆法只能处理作用位置已知且平稳的离散分布载荷。此外，落震载荷识别的另一个难点是，机体结构对基本冲击元δ函数的响应测量问题，在全尺寸结构下，点对点测量飞机对单元冲击的响应时，飞机的约束是个很大的困难，因为在真实情况下，冲击瞬间的前后，飞机的约束条件会发生变化，而在试验中很难实现约束条件的瞬间改变。本文从现有理论出发，对全机落震冲击载荷识别标定的主要技术点进行了研究。

1  结构动载荷识别的主要理论方法

目前，动载荷识别的主要方法有频域法和时域法两大类。众所周知，结构动力学的求解问题有三大类：第一类为已知激励和结构动力学参数求响应，一般称之为正问题；第二类为已知激励和响应求结构动力学参数，称之为第一类逆问题；第三类为已知结构动力学参数和响应求激励，称之为第二类逆问题。一般来说，正问题的求解是解决第二类逆问题的前提和基础。

1.1  结构动载荷识别的频域法

频域法是通过求解结构的频响函数矩阵方程，来获得结构所受载荷的频域信息，再通过时-频转换，最终获得动载荷时域信息。此方法需要首先测得结构对正弦激励的响应，其求解模型如下[7]：

假设载荷作用位置已知，待识别载荷数为Ni，测量点数Nj，以F(ω)Ni×1表示激励载荷向量，X(ω)Nj×1为响应向量，G(ω)Nj×Ni为频响函数矩阵，其每一个因子通过动载荷识别的正问题来获得，对于线性时不变系统有：

为了方程可解，一般要求Nj＞Ni，求解式（1），可得动态载荷向量为：

由此可见，通过频响函数求逆的方法，其求解过程简单，但是需要注意的是，此方法必须首先测量结构对正弦激励载荷的响应，并且载荷作用的位置也必须是已知的。总结起来，频域法在反求载荷时存在以下局限性：第一，在结构的固有频率附近，式（1）的求解容易出现病态问题；第二，在正向求解或者测试结构对正弦函数的响应时，必须对高阶激励对应的高阶模态进行舍弃，因此式（2）所给结果存在截断误差；第三，对于稳态或者平稳随机载荷的识别精度较高，对于瞬态冲击载荷识别精度较低；第四，频域法给出的结果是以频率为自变量的一系列复数，直观性比较差。

1.2  结构动载荷识别的时域法

时域法的目的是通过动态响应直接获得动载荷的时间历程。其基本思想是将时域内连续载荷离散为一系列阶跃载荷，以杜哈梅尔积分公式为基础，通过模态分解和转换的方法，最终求出由响应反求载荷的计算公式。

假设系统为具有N自由度线性时不变系统，其运动微分方程如下：

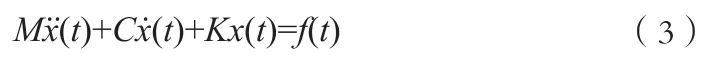
式中，M、K、C、x（t）、f（t）分别为结构的质量矩阵、刚度矩阵、阻尼矩阵、位移响应向量和外载荷向量。以模态矩阵与模态坐标表示位移响应向量：

其中，Φ为结构各阶模态向量组成的模态矩阵。将式（4）在模态坐标空间解耦，对于第r阶模态有：

式（5）中，mr、kr、cr、qr(t)、fr(t)分别为结构第r阶模态质量、模态刚度、模态阻尼、模态坐标、模态力。时域法识别的流程是：已知模态坐标响应qr(t)或，计算出模态力，根据fr(t)以及式（3）、式（5）反求f(t)。

时域法的优点是对于瞬态冲击载荷具有较好的预测结果，尤其是在做好模态分析或模态测试的基础上。缺点是建模异常复杂，求解过程没有频域法简单明了，并且由于累积误差与传递误差存在，当载荷历程较长时，预测误差较大。

2  全机落震载荷标定的技术流程

全机落震载荷标定与恒定飞行载荷标定的最大不同在于落震冲击载荷作用时间短、量级大，应变测量对于载荷的响应在时间轴上呈现出卷积效应，以公式表示如下：

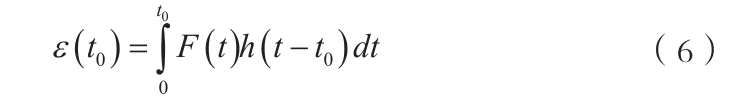
2.1  飞机动力学模型建立与模态参数测量

全机着舰过程中，甲板作用于起落架的冲击载荷垂直向上，可能造成结构破坏的载荷以冲击引起的弯矩载荷形式出现，因此在建立模型或分析载荷时，主要考虑弯矩载荷。因而将飞机简化为只考虑横向振动的悬臂梁结构。

关于飞机的约束问题，一般认为在起落架着陆撞击过程中，飞机为带弹性地基（起落架）的简支结构。撞击完成回弹过程中，机体处在兼有有刚体运动与弹性体振动的无约束状态。全机简化模型如图1所示。

若通过仿真计算获得机体模态参数，则对机体沿机身轴向、机翼展向做等刚度（弯曲刚度）等效简化，起落架与机身以弹簧-阻尼器方式简化连接。模拟飞机在重力作用下坠落到地面，压缩段支持方式为简支，回弹段可视为无约束状态。

如果通过试验手段获取整机模态参数，可考虑设计一个三点测力平台，在较低高度下进行落震试验，以获得在真实载荷激励下典型部位的响应系数矩阵。

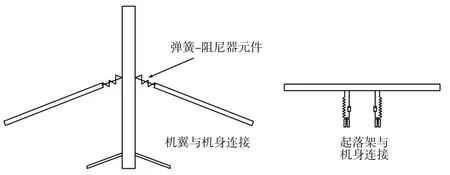
图1 机身与机翼及起落架弹性体连接示意图

2.2  落震冲击载荷特征分析

落震载荷是指全机在着舰过程中，舰船甲板对起落架的冲击载荷。一般全机垂直着舰速度最大可达到7m/s，作用时间尺度在0.5s左右。图2所示为某型机全机落震试验某对称工况左右主起落架测力平台所测载荷，数据做了归一化处理。由数据可以看出，第一次冲击载荷持续时间约0.5s，能量经过起落架吸收后，第二次冲击大幅度减小，且第二次冲击载荷上明显附加了机体自由振荡所引起的惯性载荷。由撞击所产生的惯性载荷，沿机翼展向或机身轴向传递，在中央翼盒及机翼根部剖面会形成比较严重的载荷工况，其大小由机体各站位聚集质量与连接刚度决定，其剪力、弯矩、扭矩计算公式如下：

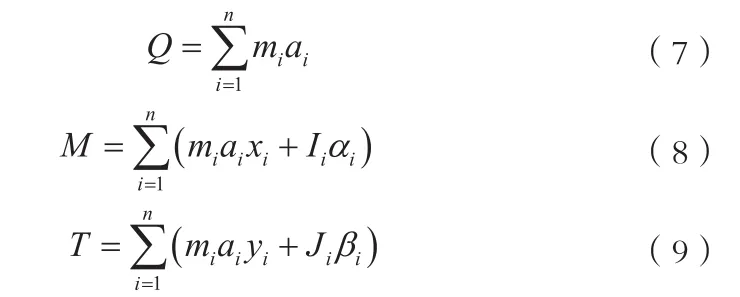
式中，Q、M、T分别为相关聚集质量累积到测量剖面的剪力、弯矩、扭矩，mi、ai、xi、Ii、αi分别为质量、第i个站位的聚集质量的垂向加速度、沿展向到测量剖面的距离、绕航向的转动惯量、绕航向的角加速度。yi、Ji、βi分别为第i个站位的聚集质量到展向转动轴的距离、绕展向转动轴的转动惯量、绕展向的角加速度。

图2 左右主起测力平台归一化数据

2.3  响应测点选择与响应特征分析

响应的测量一般位于典型剖面部位，如机翼机身某些剖面，可以是应变、位移、速度、加速度等物理量。在落震试验中，当机体受到起落架冲击后，机翼根部以外的质量由于惯性力的缘故在机翼根部可能形成引起严重后果的剪力与弯矩载荷。为了考察某截面内的弯矩、剪力、扭矩载荷，如果测量加速度响应，测点布置于剖面以外质量聚集点处。如果测量应变响应，则测点布置于剖面以内。图3是某型全机对称三点落震工况下的应变响应数据，应变测点对称分布于左右机翼3肋处，结合图2所示数据可以看出，飞机从投放到着陆的自由落体段3肋处已出现明显的应变响应，随着第一个冲击峰的到来，应变响应达到最大值，第二、三个峰值出现的时间与测力平台的载荷峰值基本一致，且左右对称性良好。不同的是3肋剖面处的应变响应数据中叠加了机体自由振动引起的响应。

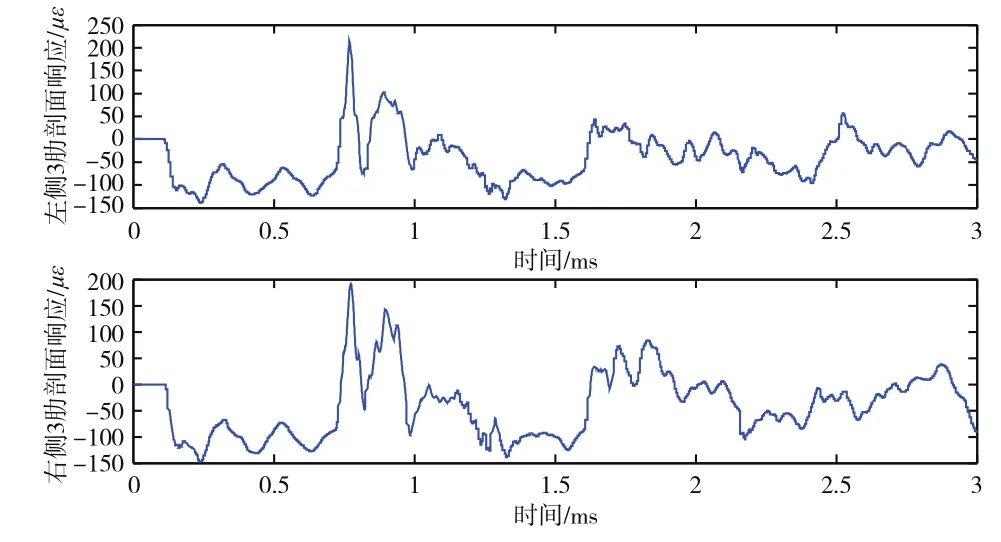
图3 某对称工况下左右机翼3肋处应变响应

对左机翼3肋应变响应做FFT分析，截取频率在32Hz以内的谐振分量，如图4所示，可以看出主要贡献的谐振频率集中在10Hz以内。因此，在进行机翼模态参数测量时，只需考虑低阶模态。

图4 左机翼3肋应变响应FFT曲线

2.4  载荷反演模型的选择

由2.2与2.3节的数据特征分析可知，在只考虑第一个冲击峰值的情况下，全机受落震载荷的冲击可看作瞬态过程，因此可采用小波分解的办法来求得剖面载荷[8]。在获得结构的频率、振型、模态弯矩、模态剪力以后，将机翼横向振动的各阶频率的过载响应或等效应变响应分量提取出来，求得机翼振动的振型函数矩阵，即可求得机翼的广义位移。再根据广义位移求得模态弯矩、剪力等，即机体在起落架冲击载荷作用下，机翼关键截面的弯矩、剪力载荷。

机翼某测量剖面处第j阶位移或等效应变响应与机翼第j阶振型及第j阶广义位移存在以下关系：

式（9）中，yj(xg)为机翼测量剖面处第j阶位移或等效应变响应，为第j阶振型向量，qj(t)为广义坐标，xg为响应测量点坐标，t为时间。显然，在求得广义位移以后，第j阶广义位移乘以第j阶模态弯矩、剪力，可得第j阶模态下的弯矩、剪力，再将各阶弯矩、剪力相加，得到总的弯矩剪力载荷。

3  总结

全机落震载荷识别属于动载荷识别的范畴，与静载荷标定识别模型不同的是，动载荷标定的理论模型与系统的结构、支持方式、外载荷特征等因素密切相关，因此在全机落震载荷识别试验中，首先要根据测量部位的结构特征与支持方式，选择合适的力学模型进行模态参数测定，这是载荷识别的最关键也是工作量最大的一个环节，其次要根据外载荷的特征选取合适的载荷反演模型。