气体吸附过程中煤比表面Gibbs函数变化规律

2019-03-27李祥春张梦婷李忠备聂百胜陈志峰

煤炭学报 2019年2期

李祥春，张梦婷，李忠备，聂百胜，陈志峰，岳超

(1.中国矿业大学(北京) 资源与安全工程学院，北京 100083; 2.中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室，北京 100083;3.河南省瓦斯地质与瓦斯治理重点实验室——省部共建国家重点实验室培育基地，河南焦作 454000; 4.新疆工程学院安全科学与工程学院，新疆乌鲁木齐 830023)

气体吸附过程是一个复杂的物理过程，煤体结构不同，煤对气体的吸附行为也不相同[1]。煤是一种孔隙、裂隙极其发育的多孔性固体介质[2]，其孔隙裂隙中或多或少的含有瓦斯气体。吸附的本质是煤体通过降低表面张力来降低比表面Gibbs函数的一种自发趋势[3]，对于气体吸附本质有不同的探讨。很多研究表明，吸附受到分子间相互作用力、结构差异等不同因素的影响，并对这种影响进行不同的探讨。聂百胜和段三明[4]认为在相同温度下，由于气体与煤表面的相互作用力的性质及大小不同而导致吸附性不同，造成吸附势垒的高低不同。降文萍等[5]证明了煤表面与瓦斯气体分子的相互电作用力导致煤吸附大量的瓦斯气体，并利用了量子化学的分子模拟方法得到煤对甲烷的吸附热为4～9 kJ/mol。崔永君等[6-7]认为煤对甲烷吸附是煤孔隙表面的分子与甲烷分子间相互吸引的结果，并且随着煤变质程度增加两者作用力逐渐减弱，温度同样影响煤的吸附。还有学者认为分子结构影响煤对气体的吸附作用，陈振宏等[8]认为煤分子化学、物理结构差异是导致不同煤阶煤层气吸附/解吸特征存在显著差异的根本原因。ABUNOWARA Mustafa等[9]通过测量不同温度下4种煤样的吸附解吸等温曲线，认为煤的吸附解吸之间存在滞后现象，吸附气体量减少。ARIUNAA Alyeksandr等[10]利用傅里叶变换红外光谱(FTIR)和核磁共振(NMR)对化学结构和功能团簇进行了分析，探究煤样对不同气体的吸附情况。描述煤对甲烷吸附行为的动力学模型主要有Langmuir单分子层理论、BET多分子层理论、吸附势理论等[11]。所以，煤的表面能是研究煤对瓦斯吸附的重要参数，其大小决定了瓦斯吸附量。许多研究都运用比表面Gibbs函数来评价气体吸附机理，并探讨不同煤样的比表面Gibbs函数差异。周来等[12-13]根据热力学理论评价了3个不同温度条件下CO2与CH4的吸附行为，并利用吸附过程中比表面Gibbs函数变化及等量吸附热差异，探讨了CO2和CH4在煤基质表面竞争吸附的机理。崔永君等[6-7]利用热力学中比表面Gibbs函数变化值评价单位面积上煤对甲烷的吸附能力，并且利用等量吸附热来评价煤与甲烷分子之间的作用力，研究发现不同变质程度煤单位面积上的吸附能力由大到小为:贫煤、焦煤、无烟煤、气煤。RUDOLPH Martin等[14]利用逆气相色谱法(iGC)确定比表面Gibbs函数分量及其颗粒表面的分布，探究比表面Gibbs函数与疏水性的关系。比表面Gibbs函数被认为是界面间的相互作用力之和，分析比表面Gibbs函数变化及其影响因素能更加深入了解吸附作用，所以很多学者对比表面Gibbs函数的性质、组分及其影响因素进行探讨。LUCYNA Holysz[15]通过研究煤的可浮选性，证明了低煤阶煤的比表面Gibbs函数既含有非极性又含有极性作用力，这种现象是由于煤中有机组分和矿物组分相互作用造成的。BRONISLAW Jadczuk等[16]使用固液界面的不同方法来计算比表面Gibbs函数，表明煤的比表面Gibbs函数的组成部分可以部分地阻挡极性组分。BURDZIK Andrea等[17]利用测量不同聚合物样品的极性SFE组分，分析用于比表面Gibbs函数的参考值。ZHANG等[18]证明气体吸附体积、煤表面结构及吸附体系温度和压力决定了表面张力的降低值，表面张力降低越大，吸附能力则越强。

目前，大多数学者都采用等温吸附实验得出气体相关吸附数据，并通过其孔隙结构、相互作用力等来分析煤吸附气体的影响因素，但是鲜有学者从吸附表面能量变化角度来探讨煤吸附气体机理。笔者通过分析吸附能量有关的计算模型及公式，利用两种煤样在4个不同温度(20，30，40，50 ℃)下的等温吸附实验数据，得到了不同煤样吸附气体过程中的能量变化规律，探讨煤吸附气体过程中能量变化与其吸附能力之间的关系及影响比表面Gibbs函数的因素。

1 等温吸附中能量计算

气体主要吸附在煤基质的孔隙表面，随着等温吸附的进行，气体分子在煤体表面吸附场中发生能量的变化，并通过一系列热力学变化反映出来，这是煤体表面分子与气体分子相互作用的宏观表现[1]。吸附势特性曲线与温度无关，而比表面Gibbs函数的计算可以反映不同温度下煤吸附甲烷能力的大小。吸附的进行建立在能量变化的基础上，通过对能量的计算来分析衡量煤吸附气体的作用，反映吸附过程中能量的变化。

比表面Gibbs函数是指在恒温恒压下，增加吸附剂单位面积时体系自由能的增量，又称表面过剩自由能或Gibbs自由能。一般认为[19]，煤是由不同的基本结构单元通过多种形式的桥键连接形成的大分子结构，其基本结构单元核由2～5个缩合芳香环或氢化芳环组成，侧链由烷基和各种官能团组成，组成煤大分子骨架的碳原子之间相互吸引处于力的平衡状态。当煤孔隙表面形成时，孔隙表面碳原子的一侧空缺造成其受力不平衡，因此受到指向煤体内部的引力作用而具有向煤体内部运动的趋势，该趋势下煤表面的碳原子获得的能量即为比表面Gibbs函数。

比表面Gibbs函数指增加单位表面积时自由能的增量，其产生的原因是由于固体表面原子(离子或分子)所处力场不对称[20]。由于煤是一种固体，其中的原子、分子间的相对运动比液体中的原子、分子困难得多，所以必须经过足够长得时间后，煤表面的碳原子才能重新达到平衡，因此，煤的表面也会发生驰豫、重构等现象[5]。由能量最低原理可知，系统的能量越低越稳定，所以煤表面在平衡过程中总是力图吸收周围其它物质以降低其比表面Gibbs函数。当孔隙中存在瓦斯气体时就会被吸附，此时煤孔隙表面附近的瓦斯气体分子吸引表面层碳原子使其较快达到平衡状态。

根据表面化学理论可知[20-22]，当瓦斯气体在煤表面上吸附时，瓦斯气体在煤表面区域的浓度一定大于煤结构内的浓度，此差值称为表面超量Γ[21]:

(1)

式中，Γ为表面超量，mol/m2;V为瓦斯吸附量，L;V0为气体摩尔体积，标准状况下为22.4 L/mol;S为煤比表面积，m2/g。

当煤吸附瓦斯气体时会引起表面张力降低，有吉布斯公式[22]:

-dσ=RTΓd(lnP)

(2)

式中，σ为表面张力，J/m2;R为普适气体常数，8.314 3 J/(mol·K);T为绝对温度，K;P为瓦斯气体压力，Pa。

将式(1)代入式(2)从瓦斯气体压力为0到P积分[23-24]得

(3)

式中，σ0为煤体在真空条件下得表面张力，J/m2。

(1)假设瓦斯吸附符合单分子层吸附Langmuir吸附方程[25]，即

(4)

式中，a，b为Langmuir吸附常数。

将式(4)代入式(3)得

(5)

由式(5)可知，煤表面张力取决于吸附量、煤的表面结构、煤-瓦斯吸附体系的温度及瓦斯气体的压力等。

对式(5)中P进行微分，得各压力点处比表面Gibbs函数变化值:

(6)

式中，VL为Langmuir体积;PL为Langmuir压力。

由于煤的单层饱和吸附量a，因此可以求出煤的比表面积[21]为

S=aNAδ/V0

(7)

式中，NA为阿伏加德罗常数;δ为吸附瓦斯气体分子的截面积，m2。

式(7)即可以计算煤的比表面Gibbs函数降低值。

(2)假设瓦斯吸附符合多分子层吸附BET吸附方程[26-27]，即

(8)

即

(9)

式中，Vm为气体单层饱和吸附量;C为与样品吸附能力有关的常数;P0气体饱和蒸汽压。

根据式(9)可求出BET吸附方程相关参数。

将式(8)代入式(3)得

(10)

对式(10)中P进行微分，得各压力点处比表面Gibbs函数变化值:

(11)

由于煤的多层饱和吸附量Vm，因此可以求出煤的比表面积[28]为

SBET=VmAσ

(12)

式中，A为吸附瓦斯气体分子的截面积，m2。

式(12)即可以计算煤的比表面Gibbs函数降低值。

2 等温吸附实验及计算分析

2.1 等温吸附实验

论文实验所需煤样分别采集于山西凤凰山矿和郑州裴沟煤矿，现场采集煤层全厚(或分层)样品，除去矸石后经过严密封装后，送至实验室。

(1)煤样的工业分析

取适量的煤样，利用SDLA618工业分析仪，根据GB/T 212—2008《煤的工业分析法》进行煤的工业分析，测定水分、灰分、挥发分等，结果见表1。

表1煤样工业分析
Table1Industrialanalysisofcoalsample%

试样名称MadVdafAdFC山西凤凰山矿3.177.098.3281.42郑州裴沟矿1.1913.4419.5965.78

(2)实验步骤

实验共取了6个平衡压力点:分别为0.2，1.2，1.5，2.5，3.0，4.0 MPa左右。

具体步骤如下:

① 设定恒温箱温度。开启温度控制系统，调节恒温箱温度控制装置，将箱内温度设定30 ℃。

② 将甲烷气瓶接入吸附装置。

③ 抽真空脱气。关闭连通大气的球阀9，打开样品罐和参考罐的所有针阀(针阀1～6)、连通气瓶的球阀7和连通真空泵的球阀8，使吸附罐、参考罐与真空系统连通，开启真空泵脱气1 h;然后先关闭所有连接罐体的针阀及连通真空泵的球阀8，再关闭真空泵。

④ 打开瓦斯吸附数据采集系统，在 “煤样设置”和“参数设置”窗口界面分别输入采集温度、罐体积等系统参数。

⑤ 待恒温箱内温度稳定在30 ℃后，打开连通吸附装置和氦气气瓶的球阀7和处于关闭状态的针阀1和针阀5，向参考罐充入甲烷气(约0.2 MPa)，调节参考罐压力值，关闭针阀5，单击吸附采集窗口上“开始采集”按钮，窗口显示1,2号罐的压力值和曲线，1,2号罐的压力分别为Pr和Ps。

⑥ 观察采集系统窗口显示的实验数据，若参考罐和样品罐压力没有较大的波动则证明气体已稳定，记录下为Pr和Ps，然后打开阀门2，使参考罐和样品罐的连通，吸附12 h后，待平衡压力稳定后，记录下1,2号罐的平衡压力为Pe。

⑦ 重复步骤⑤，⑥，直至最后一个平衡压力点实验结束。将所有实验数据都保，并将第i次的参考罐、样品罐及平衡压力记录为Pir,Pis和Pie。

(3)实验结果

根据凤凰山煤样和裴沟煤样分别在20，30，40，50 ℃下的等温吸附实验，通过计算得到基本实验数据，如图1所示。

据以上实验结果知，充气压力不同导致实测吸附量有所不同，煤样的吸附量随着压力的增高而增大。而且温度变化对于煤体瓦斯吸附能力影响较大，对于实验所用凤凰山煤矿60～80 目煤样，在充气压力相同的情况下，最终平衡压力不同。充气压力同为3 MPa左右的情况下，20，30，40，50 ℃凤凰山煤样的瓦斯吸附平衡压力分别为3.46，3.37，3.42，3.43 MPa;而裴沟煤样的瓦斯吸附平衡压力分别为3.53，3.43，3.47，3.48 MPa。平衡后凤凰山单位质量煤体的吸附量分别为34.80，30.39，29.01，26.99 mL/g，平衡后裴沟煤矿单位质量煤体的吸附量分别为21.78，20.03，18.00，14.98 mL/g。表明温度越高平衡时的瓦斯吸附量越低。随着温度的升高，煤体吸附甲烷能力变差，与卢守青等[29]研究结果一致。

从图1可以看出，相同温度条件下，凤凰山煤样比裴沟煤样吸附量大，即Langmuir体积大，反应了凤凰山煤样吸附气体的能力较大。

图1 不同温度下的等温吸附曲线Fig.1 Isothermal adsorption curves of coal sample under different temperature

2.2 能量计算结果及分析

(1)比表面Gibbs函数

根据Langmuir的单分子层吸附模型，测试出在恒温情况下煤的吸附常数a和b。甲烷气体的截面积为16.4×10-20m2[30]，由于a为煤的单层饱和吸附量，因此根据式(7)算出煤的吸附比表面积见表3。

表2煤样的Langmuir方程参数拟合结果
Table2ParameterfittingresultofLangmuirequationofcoalsample

温度/℃凤凰山煤样R2ab裴沟煤样R2ab200.989 737.037 02.076 90.998 826.109 71.285 2300.995 533.898 31.915 60.999 726.041 71.002 6400.995 833.003 31.664 80.998 125.575 40.747 6500.998 431.446 51.452 10.999 821.052 60.720 8

表3比表面积的计算结果
Table3Resultsofspecificsurfacearea

煤样比表面积/(m2· g-1)20 ℃30 ℃40 ℃50 ℃凤凰山163.24149.41145.46138.60裴沟115.08114.78112.7292.79

根据式(5)和(6)，按照单层吸附模型对不同温度下各煤样煤的比表面Gibbs函数降低值进行计算，结果见表4。

根据式(9)对方程进行拟合，得出BET吸附方程相关参数见表5。

表4比表面Gibbs函数变化值的计算结果(单层吸附模型)
Table4ResultsofspecificsurfaceGibbsfunctionvariation(monolayerabsorptionmodel)

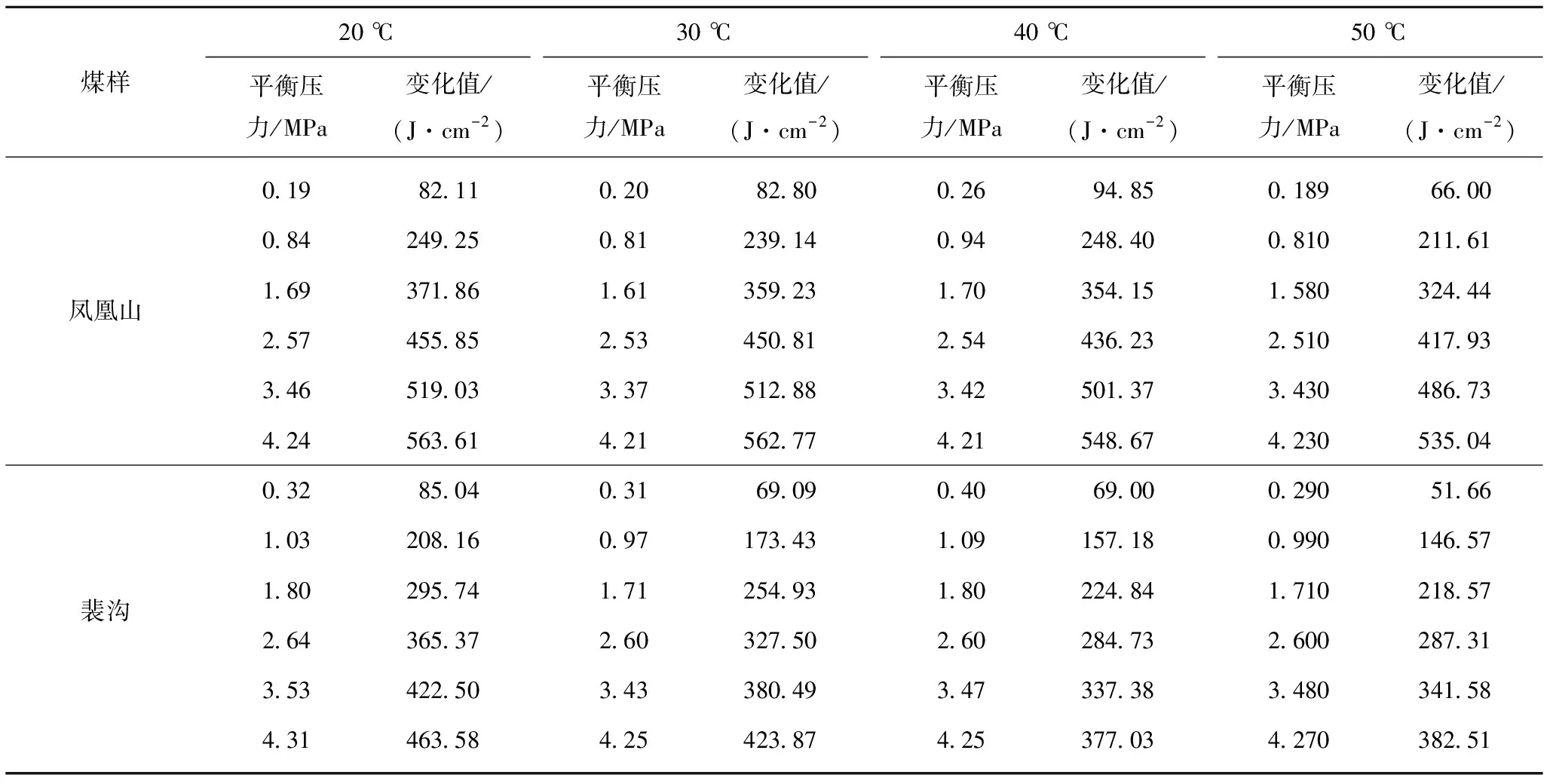
煤样20 ℃平衡压力/MPa变化值/(J·cm-2)30 ℃平衡压力/MPa变化值/(J·cm-2)40 ℃平衡压力/MPa变化值/(J·cm-2)50 ℃平衡压力/MPa变化值/(J·cm-2)0.1982.11 0.2082.80 0.2694.85 0.18966.00 0.84249.25 0.81239.14 0.94248.40 0.810211.61 凤凰山1.69371.86 1.61359.23 1.70354.15 1.580324.44 2.57455.85 2.53450.81 2.54436.23 2.510417.93 3.46519.03 3.37512.88 3.42501.37 3.430486.73 4.24563.61 4.21562.77 4.21548.67 4.230535.04 0.3285.04 0.3169.09 0.4069.00 0.29051.66 1.03208.16 0.97173.43 1.09157.18 0.990146.57 裴沟1.80295.74 1.71254.93 1.80224.84 1.710218.57 2.64365.37 2.60327.50 2.60284.73 2.600287.31 3.53422.50 3.43380.49 3.47337.38 3.480341.58 4.31463.58 4.25423.87 4.25377.03 4.270382.51

表5煤样的BET方程参数拟合结果
Table5ParameterfittingresultofBETequationofcoalsamples

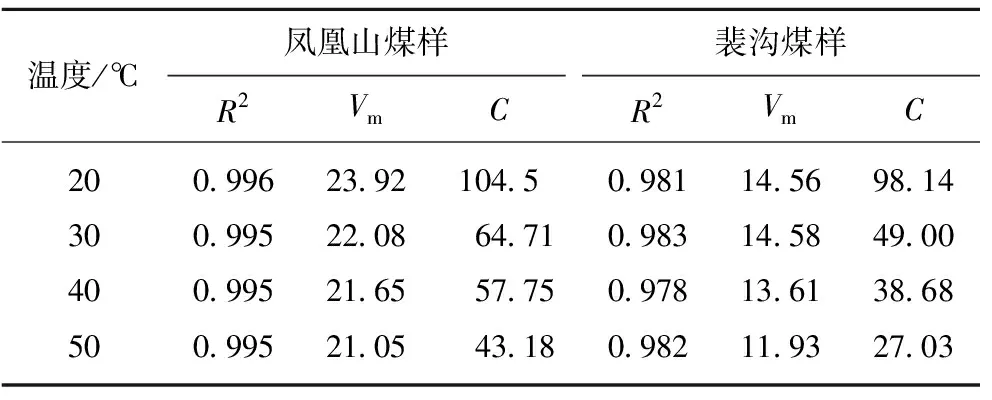
温度/℃凤凰山煤样R2VmC裴沟煤样R2VmC200.99623.92104.50.98114.5698.14300.99522.0864.710.98314.5849.00400.99521.6557.750.97813.6138.68500.99521.0543.180.98211.9327.03

根据式(10)和(11)，按照多层吸附模型对不同温度下各煤样煤的比表面Gibbs函数降低值进行计算。结果见表6。

根据实验可以得出:煤样的吸附量随着压力的增高而增大，随着温度的升高而减小，说明煤对甲烷的吸附是放热过程。随着温度的升高比表面Gibbs函数变化量减少，随着压力的升高比表面Gibbs函数变化增加，即比表面Gibbs函数变化值的大小反映了单位面积吸附甲烷量的多少。

表6比表面Gibbs函数变化值的计算结果(多层吸附模型)
Table6ResultsofspecificsurfaceGibbsfunctionvariation(multilayeradsorptionmodel)

煤样20 ℃平衡压力/MPa变化值/(J·cm-2)30 ℃平衡压力/MPa变化值/(J·cm-2)40 ℃平衡压力/MPa变化值/(J·cm-2)50 ℃平衡压力/MPa变化值/(J·cm-2)0.19120.48 0.2082.860.2689.180.18954.090.84261.48 0.81193.390.94193.730.810149.17凤凰山1.69345.41 1.61266.641.70257.371.580214.502.57402.83 2.53322.632.54306.772.510268.323.46448.83 3.37362.813.42347.873.430309.774.24484.29 4.21397.804.21379.884.230340.840.32113.24 0.3172.26 0.4067.77 0.29035.11 1.03198.86 0.97144.24 1.09127.21 0.99085.96 裴沟1.80247.91 1.71190.91 1.80165.80 1.710119.59 2.64285.81 2.60230.86 2.60198.38 2.600150.61 3.53318.21 3.43260.84 3.47227.32 3.480175.53 4.31343.34 4.25286.92 4.25250.10 4.270195.21

对比通过两种模型得到的公式计算得出的结果，相差较大。主要原因是单层吸附是将煤抽象为由碳原子构成的有机固体。煤表面的碳原子，至少有一侧是空的，因而其所受到的作用力是不饱和的，这就使表面的碳原子有向煤体内部运动的趋势[31]。使煤表面的碳原子获得一种额外的能量，即表面能。当煤体表面对气体分子产生范德华力时，即发生物理吸附。而多层吸附是从煤的有机结构分析，低、中变质阶段煤中有机质的芳香结构层很少并且是随机分布的，它由大量的含氧官能团、含氧桥和脂肪族侧键相联结和支撑[32]。随煤化程度增加,这些侧键基团逐渐脱落而成为H2O，CO2，CO，CH4等，造成煤体本身的价键和作用力的不平衡，发生吸附并产生自由能。而且对于多层吸附来说，当吸附达动态平衡时，平衡方程吸附相中每相邻两层间需满足化学势相等。第1层吸附热与第2层以上各层的吸附热有较大差别。

(2)热量

在瓦斯吸附的过程中，伴随着热量的变化，这部分热量被称为吸附热。吸附热反应了煤体表面吸附场中的能量变化，即不同势能状态的能量差。煤体瓦斯吸附过程中，在等温条件下，煤体表面上进行的瓦斯吸附是一种表面自由焓和熵均减小的过程，所以计算热量可以衡量比表面Gibbs函数的变化。

在煤体吸附解吸中伴随有煤体温度不同程度的升高，由于实验在恒温箱中进行，环境温度对吸附解吸温度有所影响。采用温度变化较敏感的阶段进行研究，根据煤体瓦斯吸附过程中温度随时间变化关系曲线可以判断，温度变化符合指数函数关系[33-34]，即

(19)

其中，ΔT为解吸温度差;α，β为拟合系数;t为吸附时间，s。经计算可得，解吸温度差与α值相差不多，α值为直线的截距，它表示时间t→∞时温度理论变化最大值，也即当瓦斯吸附平衡且系统为绝热系统时的温度变化。

根据热力学公式可以计算煤样的瓦斯吸附过程产生的热量[35]，即

ΔE=cmΔT

(20)

其中，ΔE为热量变化值，J/g;c为煤的比热容，一般取1.46 J/(K·g);m为参与作用的煤样的质量，g。热量计算结果见表7。

表72种煤样热量计算结果
Table7Resultsoftwocoalsamplecalorie

煤样20 ℃ΔT/℃ΔE/(J·g-1)30 ℃ΔT/℃ΔE/(J·g-1)40 ℃ΔT/℃ΔE/(J·g-1)50 ℃ΔT/℃ΔE/(J·g-1)2.721 191.362.641 156.322.37 1 038.06 2.31 1 011.78 8.793 850.028.633 779.948.57 3 753.70 8.31 3 640.77 凤凰山9.724 257.369.514 165.389.45 4 137.52 9.19 4 023.40 17.267 559.8817.037 459.1416.70 7 314.95 16.43 7 196.84 20.358 913.3019.978 746.8619.83 8 684.66 19.55 8 564.56 21.969 618.4821.319 333.7821.08 9 234.09 21.80 9 548.01 2.03889.141.93845.341.72753.361.64718.324.241 857.123.661 603.083.171 388.463.011 318.38裴沟5.562 435.284.812 106.784.291 879.023.981 743.249.414 121.588.643 784.328.083 539.047.833 429.5410.654 664.708.843 871.928.323 644.168.173 578.4612.095 295.4210.734 699.749.974 366.869.464 143.48

根据热量可以计算比表面Gibbs函数的变化值，结果见表8。

表8比表面Gibbs函数变化值的计算结果
Table8Resultsofsurfacefreeenergyvariation

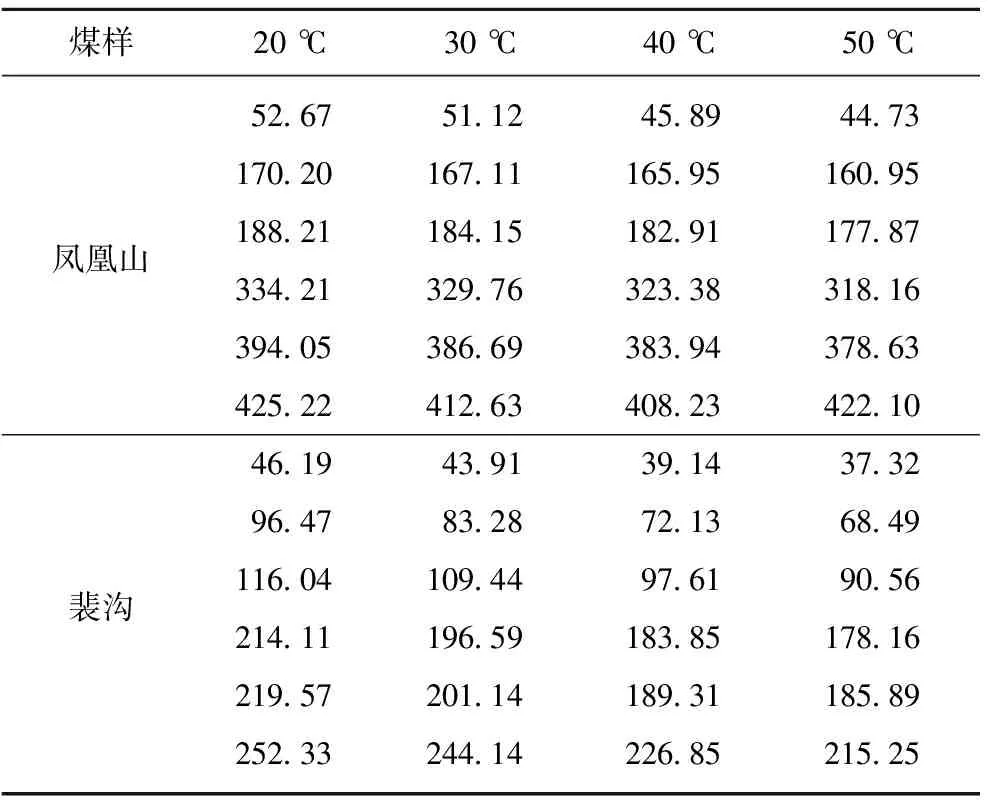
J/cm2

根据煤体吸附解吸的热量与比表面Gibbs函数变化对比可知，例如在30 ℃两种煤样吸附解吸时，数值对比如图2，3所示。

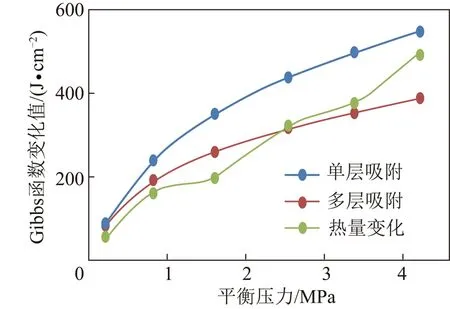
图2 30 ℃凤凰山煤样吉布斯函数对比Fig.2 Comparison of 30 ℃ Gibbs Function of Fengh-uangshan coal sample

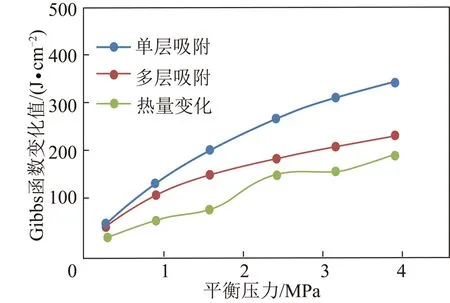
图3 30 ℃裴沟煤样吉布斯函数对比Fig.3 Comparison of 30 ℃ Gibbs Function of Peigou coal sample

根据热量计算的比表面Gibbs函数变化趋势更接近多层吸附计算结果。所以用多层吸附模型计算比表面Gibbs函数变化更加合理，比较接近现实。BET成立范围通常在P/P0=0.05～0.35，本实验充气压力符合BET吸附模型成立条件，这时表面覆盖率θ=V/Vm约为0.5～1.5。证明煤对甲烷的吸附过程比较复杂，单一用物理吸附来定义计算所得误差较大，煤样的表面吸附相互作用比吸附质分子间的相互作用力强，所以采用BET吸附模型得出的能量值更加接近实际能量变化。

对比同一温度下，两个煤样的吸附量可以发现，同一温度下，凤凰山煤样对甲烷的吸附量大于裴沟煤样。说明凤凰山煤样对甲烷的吸附作用大于裴沟煤样对甲烷的吸附作用。出现这种结果是因为两种煤样的含水量和微观结构不同。由于水分子与煤表面的作用力比较强，煤中水的存在对甲烷气体吸附影响较大。煤对水的吸附，其本质是煤分子和水分子之间的作用力使水分子在煤表面上的停留，这些作用力主要包括范德华力和氢键。研究表明，液态水会在煤岩表面形成一层水分子膜，会为甲烷分子提供相应的吸附位，造成吸附量的增加[36]。对比凤凰山和裴沟两种不同的煤样，根据表1可知，凤凰山矿水份含量较高，达3.17%，所以凤凰山矿煤样吸附能力较强。

两种煤样的吸附量不同与煤内在的官能团有关。通过红外光谱法，研究煤样的官能团类别，利用傅里叶红外光谱仪测定两种煤样的红外线光谱图，结果如图4和5所示。

图4 凤凰山煤样红外光谱Fig.4 Infrared spectrum of Fenghuangshan coal sample

图5 裴沟红外线光谱Fig.5 Infrared spectrogram of Peigou coal sample

由图4和5可以得出两种煤样所含的官能团类型基本相同，煤分子骨架以芳香核为基本结构单元，各芳香环通过不同类型桥键连接，含氧官能团、脂肪烃及各原子集团附着于煤分子骨架。

煤分子不同官能团对甲烷分子的吸附作用不同，凤凰山矿煤样中含有更多的-OH官能团、芳香烃C-H官能团、羰基化合物官能团，增加了煤体吸附瓦斯的能力。所以凤凰山煤样对甲烷的吸附作用大于裴沟煤样对甲烷的吸附作用。煤样中的官能团同样影响比表面Gibbs函数变化，不同于物理吸附的单层吸附模型，内部化学变化产生的能量导致多层吸附能量变化更接近实际变化，煤样吸附解吸是一个复杂多变的过程，通过改变其化学变化产生能量可以改变比表面Gibbs函数的变化，从而促进煤样吸附甲烷，提高瓦斯抽采效果。

3 气体吸附能量变化机理分析与探讨

根据煤样吸附甲烷后的吸附量变化值，可以看出不同煤样的比表面Gibbs函数是不同的，因此对瓦斯的吸附难易程度也不同，所以可以用比表面Gibbs函数来衡量煤的吸附能力。比表面Gibbs函数越大，说明该煤样越易吸附瓦斯，瓦斯在这样的煤层中渗流运移就越困难，对这样的煤层进行瓦斯抽放时就比较难。

使用Quantachrome Autosorb-iQ全自动比表面和孔径分布分析仪，采用低温液氮实验测得实验煤样的比表面积、孔容、孔径大小及分布等参数。经Matlab和fractalfox2.0软件对凤凰山矿及裴沟矿的实验煤样不同放大倍数的电镜扫描图片进行处理，经过计算可得出煤样的分形维数。实验结果见表8。

表82种煤样微观结构
Table8Microstructuredataoftwocoalsample

这些参数一定程度上代表着煤粒吸附能力的强弱，可根据其分析各自的微观结构特点。

对比实验数据可知，相同温度条件下，凤凰山煤样的自由能变化值比裴沟煤样的变化大，凤凰山煤样比裴沟煤样吸附量大，所以能量的变化可以反映吸附能力的大小。能量的变化受多种因素影响。能量变化受到煤样内部孔隙的影响，煤是一种含有孔隙、裂隙结构的双重孔隙结构介质[4]。通常煤基质是有多个被裂隙分割地小基质单元组成的，每个小基质外表面为裂隙通道，内部包含多个中孔或微孔结构。吸附能力可能与煤的孔径分布有关，低煤级煤，大孔隙较多，吸附较快，高煤级煤以微孔、孔容为主，吸附较慢[37]。通过分析煤样微观结构数据(表8)，凤凰山煤样内部孔隙结构连通性较好，孔隙结构复杂程度较高，孔径较小，所以吸附能力较强，即能量变化较大。裴沟煤样分形维数较大，煤样的最大吸附能力降低，说明孔隙结构越复杂，为瓦斯吸附提供的吸附位越少，越不利于瓦斯吸附，能量变化越小。

能量变化受到化学键，即分子间作用力的影响。引起煤对甲烷吸附的主要是范德华力，它包括色散力、取向力和诱导力[10]。在计算煤吸附甲烷时，“范德华力”泛指除了共价键、库伦力等较强的相互作用力之外，较弱的相互作用的总和。距离小到一定程度时，分子间作用力将变大。煤大分子表面各原子的吸附能力不同，能力强则会形成吸附空位，从而吸附甲烷分子。在漫长的煤化过程中，随着煤化程度增加构成骨架结构的环数增多，连接在骨架结构周围的侧链和含杂原子官能团数量不断变短和减少，碳含量不断提高，比表面积增加，静电力增大导致吸附能力增加[34]。如表8所示，凤凰山矿煤样比表面积为22.62 m2/g，而裴沟比表面积为19.25 m2/g，所以凤凰山比表面积较大，即其静电力较大，所以凤凰山煤样能量变化较大，吸附能力强。

气体吸附能量变化影响着吸附量的变化，而能量变化又同样受到煤样微观结构以及内部化学结构的影响。因此，可以从改变能量的角度去探讨如何影响瓦斯解吸，达到提高瓦斯抽采效果的目的。