多约束下距离加权最优滑模末制导律

李宏宇,王旭刚,华思雨

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

制导炮弹的出现使“战争之神”的火炮具有纵深精确打击高附加值点目标的能力,大大加强了火炮的压制水平和毁伤能力。近年来,作战领域越来越广,制导要求越来越多,为达到“远、准、狠”的要求,众多国内外学者对制导律展开了研究[1-2]。末制导炮弹制导最重要的作战指标就是达到理想的落点与落角,但是在末制导过程中有许多其他因素限制,如末制导炮弹自身决定的最大可用过载、导引头视线角限制、攻角约束等限制,使得制导效果难以实现,所以为达到好的制导效果,多约束下末制导律的研究势在必行。

文献[3]在目标函数中用罚函数代替终点限制条件,推导出一种能命中目标并保证大落角的最优制导律;文献[4]在实现具有指定碰撞角和零终端脱靶量的最优制导律的同时讨论了初始航向角的影响,给出了初始航向角和末次迎角的捕获区域;文献[5]推导了一种特定冲击角和零终端脱靶量的最优制导律,提出了考虑路径曲率的实用时间计算方法;文献[6]提出了一种恒速导弹对静止目标的脱靶量和冲击角终端约束的最优制导律,提出剩余时间加权函数,通过改变权数来改变弹道轨迹;文献[7]提出了一种关于剩余弹目相对距离加权函数的带落角约束的末制导方法。

为增强制导律的精确性,本文根据文献[7],将剩余相对距离的权函数加入到制导律推导中,改变权数可以改变制导炮弹的运动轨迹,随着权数的增大,运动轨迹变弯曲,制导时间增长,增大制导空间及时间,有利于提高制导律的精确度,达到更精确的落角、落点等要求。但轨迹过于弯曲会带来过载以及导引头视线角等约束问题,对此本文提出在导引头视线约束与过载约束下的最优末制导律,在文献[7]的基础上通过变权法解决大权数带来的过载及导引头视线角约束问题。理论上最优末制导律能实现很好的打击效果,但在实际工程应用中,制导炮弹不可避免地会受到各种扰动的影响,飞行中受到风、温度、气流变化等外界因素的干扰和空气动力变化的影响,同时导引头/惯导的测量信息和估计信号存在偏差和噪声,在这些干扰和摄动的作用下,弹目运动方程不可避免地存在着参数的不确定性[8],这种情况单纯使用最优制导律会发生较大且不可估计的误差,所以为了增强最优末制导律的鲁棒性,在最优末制导律的基础上引入滑模变结构控制理论。

1 动力学模型

本文研究的制导炮弹的攻击目标一般为静止或运动速度不超过25 m/s,所以本文中假设目标静止,以末制导阶段开始时刻制导炮弹M在目标T所在水平面内投影点为原点O,投影线为Oy轴,原点与目标的连线为Ox轴,弹目相对几何关系如图1所示[9],图中,r为弹目相对视线距离;v,a分别为制导炮弹的速度和加速度;θ为俯仰角;σ为导引头视线角;q为弹目视线连线角;θf为末端约束角。

根据图1弹目基本关系,可得非线性运动学方程组[10]:

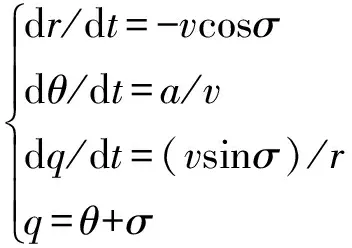
(1)

制导炮弹的状态方程一般可用状态空间方程组表示:

(2)

式中:x=(x1x2…xn)T,表示状态矩阵;A,B为系数矩阵;u为控制矩阵。

图1 弹目基本几何关系

本文取状态变量为:x1=σ,x2=θ;控制变量为:u=a,假设σ很小,且σ<π/2,(t∈[t0,tf]),其中,t0为末制导开始时刻,tf为末制导结束时刻,通常取t0=0,tf即为末制导时间。将状态变量转化为对弹目相对距离的函数,可得到状态方程:

(3)

假设初始时刻t=0的状态量为r=r0，末端时刻t=tf时,r=0,则以r为变量,弹目相对距离的边界条件为

x1(r0)=σ0,x2(r0)=θ0,x1(0)=σf,x2(0)=θf

(4)

式中:r0为状态量,下标0表示初始时刻状态值,f表示末端时刻状态值。

2 剩余行程加权最优制导法

制导炮弹末制导段炮弹法向过载与攻角之间近似满足关系式[11]:

ny=(v/g)a4α

(5)

式中:α为攻角,a4为系数。

从式(5)中可看出过载与攻角成正比。本文在小攻角的情况下进行研究。一般带落角约束的最优末制导律的加速度指令基本呈线性变化,制导开始一瞬间或击中目标瞬间加速度指令达到最大。将距离权数的倒数加入到性能指标方程中,可使制导在开始阶段的加速度指令增大。所以最优制导指令中加入权函数后加速度先增大后减小,最后慢慢收敛到0,随之攻角也收敛到0。

将距离加权函数加入到最优制导律推导过程中,通过改变权数改变制导炮弹的运动轨迹、运动时间,改变制导结果。

能量最优的性能指标方程:

(6)

式中:M(r)表示正权函数。

M(r)=1/rN

(7)

式中:N≥0,表示制导增益,即权数。

用变分法求解[12]。构造哈密顿函数:

(8)

式中:λ1,λ2表示共态变量。

协态方程:

(9)

极值条件:

-∂H/∂u=a/rN-λ1/v2-λ2/v2=0

(10)

末端约束方程:

ψ[x(tf),tf]=x2(tf)-θf=0

(11)

横截条件:

(12)

式中:γ1,γ2为待定拉格朗日乘子,不变分。

结合式(9)和式(12)得:

λ1=γ3r,λ2=γ2

(13)

式中:γ3为关于r的待定函数。

将式(13)代入式(2)积分,得到σ,θ表达式,再分别代入式(4)的初态、末态,可得到γ2,γ3表达式,将其代入式(10)整理得[7]:

(14)

tgo=r/(vcosσ)≈r/v

(15)

式中:tgo表示剩余制导时间。

将式(15)代入式(13)得:

(16)

3 分段制导

加权最优制导律中,增大权数可以使制导炮弹的轨迹明显变弯曲,制导时间加长,给制导更多的时间与运动范围,使制导精度增大。但是由于制导炮弹与导引头本身的特性限制,轨迹过于弯曲会引起过载超载以及导引头视线丢失,导致制导失败[13]。所以,为了既满足过载与导引头视线角的约束又增强制导效果,本文采用分段制导法,加入权函数之后,加速度以及导引头视线角在初始阶段达到最大再逐渐收敛到0。最大值在前期达到,所以先采用小的权数的制导律,满足过载以及导引头视线角约束,后期再转换成大的权数,提高制导精度:

(17)

式中:N1,N2分别代表制导过程中不同阶段的不同权数;rc为末制导律转化点,即r=rc时转换末制导律。

为了不同权数的制导律转换的平滑性,设2个权数不同的制导律过载相等的点为转换点,即aN1(rc)=aN2(rc)。

4 加权最优滑模制导律

最优制导律在理论上可以很好地满足制导精度,但是在制导炮弹的实际工作中,由于制导环境的不确定性,制导过程中或多或少存在一定的干扰,所以为增强制导炮弹的鲁棒性,在最优控制理论基础上加入滑模控制策略思想,构造适当的滑模平面和趋近律,得到一种既满足脱靶量、落角等多约束条件又有较强鲁棒性的最优滑模制导律[14]。

(18)

式中:k1为常数。将式(14)代入式(2)得到:

(19)

根据文献[15],构造最优滑模趋近律的一般模式:

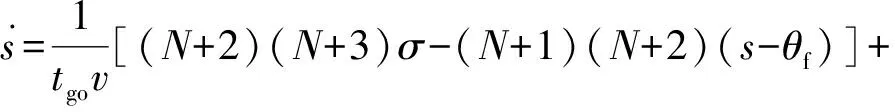
(20)

式中:ε为趋近律微分方程中的系数。

将式(14)、式(17)代入式(2)得:

(21)

下面根据Lyapunov理论证明所推导制导律的稳定性[13]。要使s→0,设v=s2/2,

(22)

因为x1,x2有界,所以设|x1x2|≤Δ6,θ,|x2|≤Δθ,等式右边第二项一定不小于0,所以有:

(23)

ε<-[(N+2)(N+3)Δ6,θ]/(vΔθ)

(24)

5 模拟仿真

5.1 不同权数的最优制导律

取权数N为0～4进行对比仿真,初始条件下,制导炮弹速度为300 m/s,相对末制导初始时刻制导炮弹相对坐标为(0,3 000)(单位:m),目标相对坐标为(5 000,0)(单位:m),初始弹道角θ0=0°,末端落角约束θf=-75°,仿真结果如表1和图2～图4所示。

表1 不同权数最优制导律的制导效果

图2 不同权数制导炮弹运动轨迹

从表1可以看出,随着权数的增大,制导时间增长,制导精度增加,脱靶量明显减小。从图2可以看出,随着权数的增大,制导炮弹的运动轨迹越来越弯曲。由图3、图4可看出,随着权数的增大,导引头视线角与过载越来越大。在实际应用中,导引头最大视线角与制导炮弹可用过载都是有限制的。可用过载为加速度除以重力加速度,本文定义约束分别为σmax=π/2和ny,max=5。有了约束的限制,权数的选择就有了限制。为了既加强制导精度又满足约束限制,可采用分段制导律。

图3 不同权数制导炮弹的导引头视线角

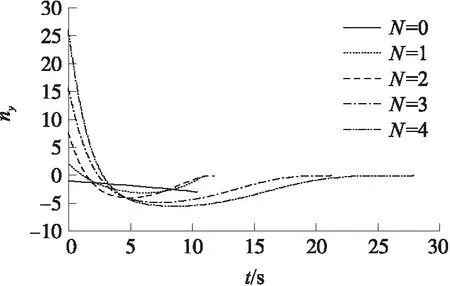
图4 不同权数制导炮弹的过载

5.2 分段制导律

由图2、图3可看出,视线角与过载均先增大,在前期达到最大值后逐渐递减到0,所以为满足过载以及导引头视线角约束,采用分段制导,在前段采用过载与视线角均在约束范围内的权数较小的制导律,当过载与视线角减小足够的小值后,转换为权数较大的制导律。初始条件见5.1,仿真结果如表2及图5～图8所示。

表2 不同制导律在干扰下的制导效果

图5 不同权数及分段制导律的轨迹对比

图6 不同权数及分段制导律的过载对比

图7 不同权数及分段制导律的导引头视线角对比

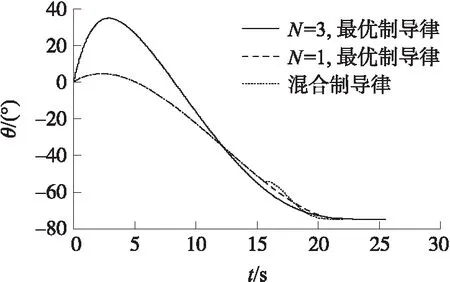
图8 不同权数及分段制导律的弹道倾角对比

从图5可以看出,在制导律转换点明显存在弯曲,弧度变大。由图6、图7可以得出,在转换点加速度与视线角均增大,但是由于基数小,变化后依然在允许范围内。由图8可知,在转换制导律后,依然可以很好地达到落角约束。

5.3 滑模最优分段制导律

图9 干扰下不同制导律过载对比

由图9可以看出,在高斯白噪声的干扰下,滑模最优末制导律的过载曲线相对更圆滑,即制导更加稳定;由表2可知,滑膜最优末制导律的脱靶量与落角均优于最优末制导律,鲁棒性增强。

6 结束语

本文为稳定末制导律的制导效果,在末制导过程中考虑导引头视线角约束与过载约束,在加权最优末制导律上加入分段制导思想,实现约束。经仿真可看出,本文推导的分段制导可以达到既满足视线角与可用过载的约束又增加精确度的要求。针对最优末制导律鲁棒性较差的不足,结合滑模变结构控制理论,在设计推导过程中加入了滑模项,使制导律具有鲁棒性,仿真结果也验证了其良好的鲁棒性。