宽速域变构型高超声速飞行器气动特性研究①

2019-03-27张登成张艳华郑无计

固体火箭技术 2019年1期

张登成，罗浩，张艳华，郑无计

(空军工程大学航空工程学院，西安 710038)

0 引言

随着双模态冲压发动机技术和高超声速飞行器一体化技术的发展成熟，组合动力、水平起降、全速域飞行的高超声速飞行器已经成为当前研究的热点。这种高超声速飞行器可以从地面起飞，经历低速、跨声速、超声速和高超声速等多个飞行阶段。因此，这类飞行器除了要保证高超声速气动特性，还要兼顾低/跨/超声速的气动特性，能在更宽的速域范围内均具有良好的气动特性。

然而，传统的高超声速飞行器大多采用旋成体、乘波体和升力体等气动构型[1]，这些构型往往只考虑了高超声速气动特性，无法满足低速、跨声速和超声速的气动特性要求。因此，合理的变构型设计对解决高超声速飞行器在不同飞行速度下的气动要求矛盾、实现全速域飞行具有重要意义。

以美国为代表的航天大国在高超声速方面的研究一直处于领先地位，开展了一系列高超声速飞行器实验，实验的飞行器种类繁多，包括外形简单的旋成体、大升阻比的乘波体以及平衡气动加热和升阻比的升力体等。其中，洛马公司近年来研制的SR-72高超声速飞行器最具代表性，该飞行器以吸气式双模态组合发动机为动力、采用水平起降的方式实现高超声速飞行，其大后掠角三角翼的翼身融合布局有利于兼顾低/跨/超声速气动特性，可以进行宽速域飞行[2]。

近年来，国内的高超声速飞行器发展也非常迅速，建立了高超声速风洞，开展了一些高超声速地面试验，取得了巨大成果。从发展趋势来看，未来高超声速飞行器更倾向于组合动力、水平起降、全速域飞行的空天飞机。国内关于宽速域高超声速飞行器的研究主要集中在通过对乘波体等固定构型飞行器的优化设计、拼接组合来提升低速时的气动特性，实现宽速域飞行[3-8]。国外的高超声速飞行器研究主要是基于先进的推进技术来设计兼顾低/跨/超声速气动特性的可重复使用的有翼高超声速飞行器[9-11]。

连接翼布局飞行器具有结构质量轻、诱导阻力小、升力系数大等优点，逐渐受到国内外研究者的重视。国内外对连接翼布局的气动特性和结构进行了大量研究，并提出了连翼布局应用于多种用途机型的方案[11-13]。国内研究的“翔龙”无人侦察机采用了连接翼的气动布局，这种布局的升阻比高、结构受力合理、有利于高亚声速飞行[14]。美国的“钻石背”炸弹也采用了连接翼布局，提高了炸弹的升阻比，扩大了打击范围[15]。

这些固定翼布局的高超声速飞行器可以在某些状态下达到较好的气动特性，但很难实现全速域范围内都有良好的气动特性，低速性能的改善都牺牲了部分高超声速性能。本文在高超声速乘波体飞行器的基础上，利用连接翼布局在低速时的优良气动特性，设计了一种宽速域变构型高超声速飞行器，解决了高超声速和低速对高升阻比和高升力外形需求的矛盾。结果表明，该飞行器在全速域范围内均有较好的气动特性，可实现宽速域飞行。

1 计算模型与数值方法

1.1 计算模型

本文设计的宽速域乘波体机身加可变菱形连接翼气动构型前后连翼的掠角和展弦比可根据不同的任务剖面自主改变，使其在不同的飞行速度下都具有良好的气动特性。在低速时，飞行器为大展弦比、小掠角的菱形连翼布局，可以快速完成爬升；在超声速时，飞行器为小展弦比、大掠角的菱形连翼布局，完成速度的快速提升；在高超声速时，连接翼收回机身内，飞行器整体上是类乘波体构型，进行高超声速巡航。变构型高超声速飞行器通过连接翼在不同飞行阶段适时的变化，兼顾了低、跨、超和高超声速的气动特性，使飞行器在各阶段都有较好的气动特性。

飞行器在三个典型状态下的气动布局示意图和模型参数分别入如图1和表1所示。

(a)低速 (b)超声速 (c)高超声速

参数低速超声速高超声速机长/mm295029502950机宽/mm658658658展长/mm45102774—前翼后掠角/(゜)1956—后翼前掠角/(゜)6830—展弦比147—

1.2 数值方法与算例验证

标准的k-ε模型是个半经验公式，主要是基于湍流动能和扩散率。k方程是个精确方程，ε方程是由经验公式导出的方程[16]。标准模型的湍流动能k和湍流耗散的输运方程如式(1)和式(2)所示：

(1)

(2)

式中ρ为密度；t为时间；ui为时均速度；xi和xj为速度分量；μ为粘度，μt为湍动粘度；Gk为由平均速度梯度引起的湍动能k的产生项；Gb为由浮力引起的湍动能k的产生项；YM表示可压湍流中脉动扩张的贡献；C1ε、C2ε和C3ε为经验常数；σk和σε分别为与湍动能k和耗散率ε对应的Prandtl数；Sk和Sε为用户定义的源项。

RNGk-ε模型是从瞬态N-S方程中推出来的，和标准模型有很多相似的地方，主要有以下改进：(1)RNGk-ε模型在ε方程中加了一个条件，有效改善了精度；(2)标准k-ε模型是一种高雷诺数的模型，而RNGk-ε模型提供了一个考虑低雷诺数流动黏性的解析公式[16]。对于高空低雷诺数条件下的数值计算，RNGk-ε模型有较高的精度。

在低速/超声速和高超声速数值计算中分别采用标准k-ε模型和RNGk-ε模型，采用无滑移和绝热的壁面条件，边界条件为压力源场，气体为热理想气体，当残差下降到10-3量级时可认为计算收敛。

数值计算的结果与湍流模型、计算网格和离散方式等多种因素有关，为验证本文采用数值方法的可靠性，分别对文献[13]中的三角翼连接翼布局和文献[17]中的类HTV-2模型进行数值计算，并与实验结果进行比较。从图2(a)、(b)的升力系数对比可看出，低速和高超声速条件下升力系数随攻角变化的实验值和数值计算结果吻合度较高、误差很小。因此，认为本文所采用的数值计算方法是可靠的。

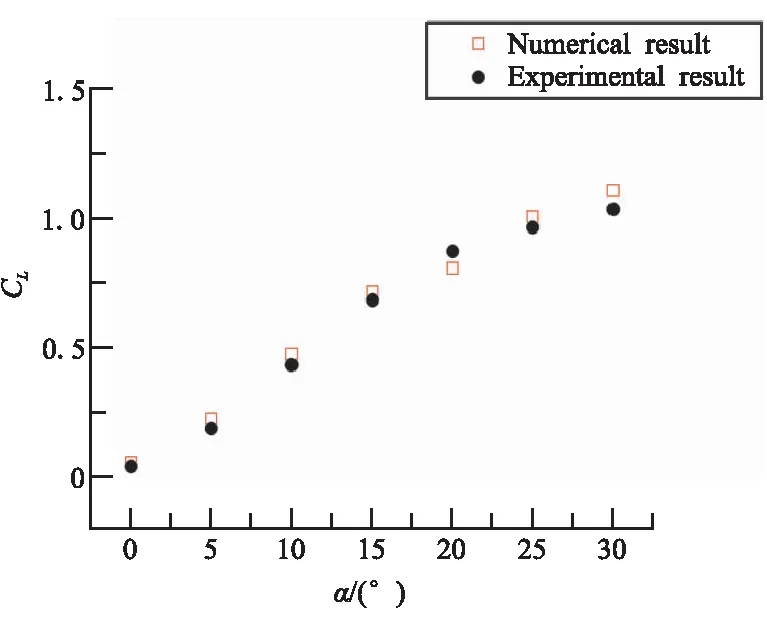
(a)低速升力系数对比

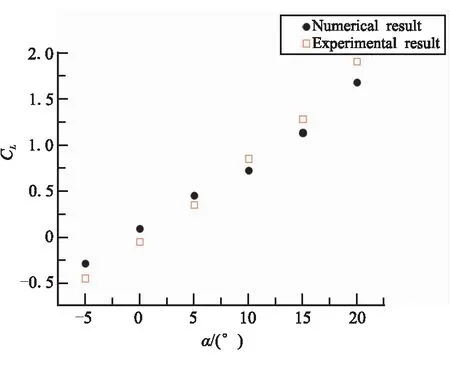
(b)高超声速升力系数对比

2 低速气动特性分析

2.1 气动特性分析

由于飞行器几何外形复杂，故本文计算中采用适应性较好的非结构网格,运用八叉树法生成四面体网格。为确保计算的准确性和提高计算效率，根据不同的空间尺寸和几何特征对飞行器的关键部位进行局部加密，并进行网格的无关性验证。低速条件下以马赫数0.3、高度1 km、攻角10°为计算条件，对网格数量分别为600万、700万、800万的三组网格划分方法的升力系数进行计算，计算结果分别为0.665、0.672、0.658，三组网格之间的最大相对误差均不超过2%,考虑到计算机的计算能力，最终采用网格数量为600万的网格划分方法，生成的网格如图3所示。对飞行器在攻角0～25°范围内每间隔5°进行计算。计算条件参数见表2。

图3 低速计算网格Fig.3 Low speed calculation grids

马赫数高度/km边界条件湍流模型离散方式0.3/0.4/0.51压力源场标准二阶迎风

图4给出了马赫数为0.3、0.4和0.5时飞行器的气动特性随攻角的变化规律。如图4所示，升力系数随攻角的增加而增大，当攻角大于10°时，升力系数曲线斜率减小；随着攻角的增加阻力系数也不断增大，但与升力系数增加过程相反，开始时阻力系数增加较慢，当攻角大于15°时突然快速增大；升阻比随着攻角的增加先增大后减小，在攻角为15°时升阻比达到最大值15.37，在大攻角范围内，升阻比也基本保持在10以上。这是因为随着攻角不断增加，机翼表面气流分离越来越严重，导致升力系数增加量较小，压差阻力快速增加，阻力系数的增加也随之加快。

从图4可看出，同一攻角下随着马赫数的增加，升力系数、阻力系数和升阻比都增大，不同马赫数下三者的变化趋势基本一致，升力系数的增加幅度相对较大，阻力系数和升阻比变化较小。

2.2 典型流场分析

图5给出了飞行马赫数为0.3，攻角为5°时的流场状态云图。图5(a)和图5(b)分别为纵向对称面压力云图和连接翼压力云图。可看出，机身下表面压力要高于上表面，产生了压力差，头部下表面压力相对较高，机身头部产生的升力对增大升阻比有一定效果。前后翼上下表面均有明显的压力差，都产生了升力，但前翼上表面的压力更小，压力差更大，提供的升力更多。前后连接翼采用“正交错”的结构由连接小翼进行连接，这样有效地减小了后翼的诱导阻力。

(a)升力系数曲线 (b)阻力系数曲线 (c)升阻比曲线

(a)对称面压力云图 (b)连接翼压力云图

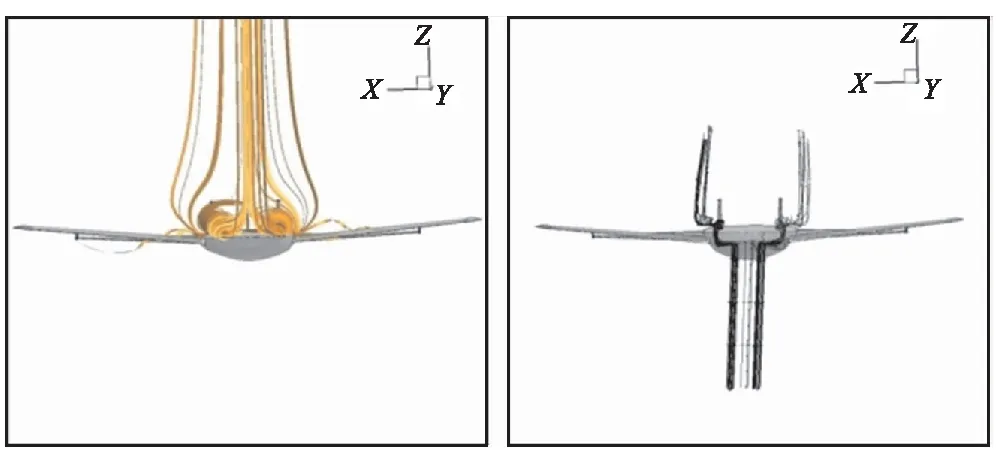
(c)涡流图 (d)流线图

图5(c)、(d)分别给出了涡流图和流线图。可看到沿着机身上表面两侧缘处产生了对称的涡结构，涡沿着机身侧缘向后延伸，机身侧缘从前到后产生了涡升力。涡诱导产生的低压区吸附在上表面，形成了附加升力，从而提高了升力和升阻比。随着攻角的增加，涡的强度和范围增大，上表面的低压区越加明显，对升力和升阻比的贡献越大；当攻角过大时，涡开始破碎，出现了气流分离，涡升力减小、诱导阻力变大。

图4中的WX6线表示文献[6]中双向飞翼飞行器在低速时的对应参数曲线图。对比双向飞翼构型,本文所设计飞行器的升力系数、阻力系数相对较大,最大升阻比小于双向飞翼构型,但最大升阻比对应的攻角明显大于双向飞翼构型,失速攻角更大。总的来说,该飞行器在低速时的气动特性较好。

3 超声速气动特性分析

3.1 气动特性分析

超声速条件下计算网格生成方法与低速时一样并进行网格的无关性验证。以马赫数1.5、高度10 km、攻角8°为计算条件，对网格数量分别为300万、450万、500万的三组网格划分方法的升力系数进行计算，计算结果分别为0.653、0.695、0.687，第一组网格与第二、三组网格之间的相对误差分别为6%、5%，第二、三组网格之间的相对误差为1%。

可见，第二、三组网格的误差较小，最终确定网格数量为450万，生成的网格如图6所示。超声速飞行时，对飞行器在攻角0～12°范围内每间隔2°进行计算。计算条件参数见表3。

图6 超声速计算网格Fig.6 Supersonic speed calculation grids

马赫数高度/km边界条件湍流模型离散方式1.5/1.6/1.710压力源场标准k-ε二阶迎风

图7给出了马赫数为1.5、1.6和1.7时飞行器的气动特性随攻角的变化规律。可见，升力系数随攻角的增加而线性增大，阻力系数与升力系数变化趋势一样，但呈现出非线性特性；升阻比随着攻角增加先增大后减小，当攻角为10°时，升阻比达到最大值4.8。

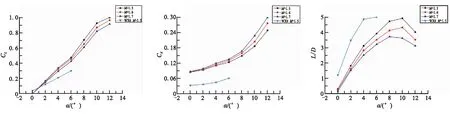
(a)升力系数曲线 (b)阻力系数曲线 (c)升阻比曲线

由图7可见，同一攻角下随着马赫数增加，升力系数和升阻比减小、阻力系数增大；不同马赫数下升力系数减小幅度较小，而阻力系数增加幅度较大，导致升阻比变化幅度较大。这是由于超声速时，随着马赫数增加，激波阻力快速增加，造成阻力系数和升阻比出现大幅变化。

3.2 典型流场分析

图8为4°攻角及马赫数分别为1.5、1.6和1.7时的马赫数云图和压力云图。从马赫数云图可见，连接翼和尾翼都产生了激波，连接翼的前翼和后翼的激波相互干扰，前翼的激波强度大于后翼，尾翼的激波强度相对最小；随着马赫数的增加，激波强度也不断增大。

对比压力云图，前翼的激波阻力远大于后翼，尾翼也产生了一定的激波阻力，前翼是阻力的主要来源；随着马赫数的增加，激波阻力明显增大。前翼上表面产生了低压区，提供了飞行器的主要升力，但也产生了相当大的激波阻力。因此，随着马赫数的增加，升阻比减小。

图7中的WX6线表示文献[6]中双向飞翼飞行器在超声速时的对应参数曲线图。相比而言，本文所设计飞行器的阻力系数明显大于双向飞翼构型，但最大升阻比略大于双向飞翼布局且对应的攻角更大，在大攻角时，气动性能明显好于双向飞翼构型。

4 高超声速气动特性分析

4.1 气动特性分析

高超声速时计算网格生成方法与低速时相同，并对网格进行无关性验证。以马赫数5、高度25 km、攻角8°为计算条件，对网格数量分别为200万、300万、400万的三组网格划分方法的升力系数进行计算，计算结果分别为0.114、0.117、0.135。可见，第一、二组网格间的误差较小，最终确定网格数量为300万，生成的网格如图9所示。对飞行器在攻角-2～10°范围内每间隔2°进行计算。计算条件参数见表4。

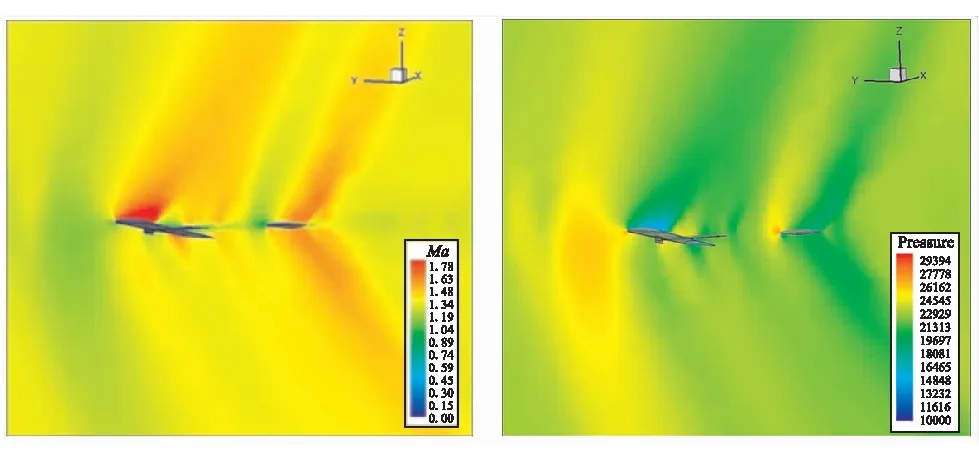
(a)Ma=1.5

(b)Ma=1.6

(c)Ma=1.7

图9 高超声速计算网格Fig.9 Hypersonic speed calculation grids

马赫数高度/km 边界条件湍流模型离散方式5/6/725压力源场标准k-ε二阶迎风

图10给出了飞行马赫数为5、6和7时飞行器的气动特性随攻角的变化规律。可见，升力系数随着攻角的增加线性增大，攻角为负角度时升力系数为负值；随着攻角增加阻力系数非线性增大，当攻角大于4°时，阻力系数急剧增大。这是由于当攻角增加时，下表面气流受到的压缩越来越剧烈，上下表面的压力差不断增大，升力系数线性增大，同时攻角的增加使激波的附体特性发生改变，使得激波阻力增加。从图10(c)升阻比曲线图可看出，随着攻角增加升阻比先增大、后减小，攻角在4°～10°范围内升阻比保持在较高的数值；当攻角为8°时，升阻比达到最大值4.08。从图10可看出，同一攻角下随着马赫数增加，升力系数、阻力系数和升阻比都减小，这与低速飞行时参数的变化趋势刚好相反，这是飞行器的乘波特性造成的。

(a)升力系数曲线 (b)阻力系数曲线 (c)升阻比曲线

4.2 典型流场分析

图11给出了飞行马赫数为6、攻角为4°时的流场状态云图。图11(a)、(b)分别给出了纵向对称面压力云图和横向截面马赫数云图。从图11(a)可看出，机身头部产生了高压区，上表面除机头处有扰动外其余部分为自由来流，压力分布均匀、流场稳定。因此，上下表面产生了稳定的压力差，提供了升力。从图11(b)可看出，飞行器的头部产生了激波，激波较好地依附在前缘线上，阻止了下表面高压气流向上表面泄漏，乘波效应明显。但由于存在黏性效应也有部分气流向上表面泄漏，导致产生的高压区有部分中断。

图11(c)、(d)分别给出了头部压力云图和尾翼压力云图。可看出，头部上下表面的压力变化都很平缓，上下压力有明显的分界线，产生的压力差很明显、升力很大，乘波效果显著。尾翼对气流有强烈的扰动，产生了较大的激波阻力，这也是升阻比降低的重要原因。这说明虽然尾翼有助于提高飞行器的操纵性，但以牺牲升阻比为代价的，在设计时需要综合考虑。