多天线无线传感器移动通信网络的物理层安全性能∗
2019-03-26徐凌伟廖建庆肖建辉
王 涵,徐凌伟,廖建庆,肖建辉
(1.宜春学院物理科学与工程技术学院,江西宜春336000;2.青岛科技大学信息科学技术学院,山东青岛266061)
近年来,随着无线通信、传感器技术、嵌入式应用和微电子技术的发展,促使国内外工业和学术界广泛的研究无线传感器网络[1-3]。伴随着移动物联网技术的发展[4-6],尤其低功耗大连接和低时延高可靠业务,促进了移动通信技术的发展。但是现在4G网络的传输速度并不能实现真正的“万物互联”,无法解决海量无线通信需求,这促进了第五代移动通信技术的发展。第五代移动通信系统支持高达10 Gbyte/s的数据传输速度,同时支持多种不同场景的通信,可以实现真正的“万物互联”[7-8]。
但是由于完全开放的信道,无线传感器通信网络的物理层安全研究非常复杂,是一个亟待解决的关键问题[9-10]。国内外学术界在各个方面对物理层安全技术展开了分析研究[11-13]。
多天线技术是一种提高通信安全性能的有效方法。苏格兰爱丁堡大学的Sarkar M Z I等人研究了在Rayleigh信道下多天线系统的安全通信[14]。在Rayleigh信道下,巴西联邦理工大学Alves H等人研究了多天线系统的安全中断概率SOP(Secrecy Outage Probability)的闭式解析表示式[15]。在此基础上,存在多个窃听节点时,可使用发送天线选择TAS(Transmit Antenna Selection)策略,Alves H等人研究了该策略系统ASC、SOP和PNSC的闭式表达式[16]。针对被动窃听场景,采用TAS策略,澳大利亚国立大学的Yang N等人研究了多天线系统的SOP的准确和近似表达式[17]。北京邮电大学的李娜等人研究了基于Rayleigh信道的多用户MIMO系统的保密传输性能,推导了遍历保密速率的闭合表达式[18]。张亚军等人针对物理层安全研究中波束成形技术的高复杂度和TAS技术的低性能,提出了一种联合人工噪声和TAS的方法[19]。重庆大学的雷宏江博士研究了基于Generalized-K信道的多天线系统的物理层安全性能,推导了SOP的近似表示式[20]。文献[21]中,作者为了确保整个传输过程中的保密性能,基于混合信号提出了一种保密传输方法。为提升非可信中继系统安全性能,文献[22]提出了一种多天线全双工目的节点加扰策略。
Rayleigh,Nakagami等信道是现有物理层安全性能的分析研究的重点。实验数据和理论分析都表明,对于实际环境中的移动通信信道,其动态特性用Rayleigh等信道不能实现很好地解释,2-Nakagami信道由于能够更灵活地表征无线移动信道衰落特征,适用范围更加广泛[23-26]。所以本文在2-Nakagami信道下,建立了多天线无线传感器移动通信网络模型。为了能够量化地分析系统的性能,本文把SOP当作量化指标。针对最佳天线选择算法和次最佳天线选择算法,本文分别推导了SOP的精确表达式。对于最佳天线选择算法,推导了其SOP下界的闭合表达式。然后在不同条件下,利用Monte-Carlo仿真验证分析了物理层安全性能。

图1 多天线无线传感器通信网络模型
1 系统模型
图1给出了多天线无线传感器通信网络模型。移动信源(S)节点发送信息给移动合法目的端(D)节点,同时会被移动窃听者(E)节点通过窃听信道获取。S使用Nt根发射天线,D和E使用单天线接收。
本文用2-Nakagami分布表示信道增益h

这里,al是Nakagami变量,它的概率密度函数为
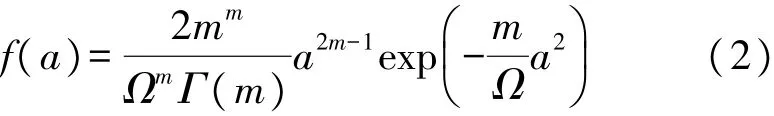
m 表示衰弱系数,Ω=E[|a|2],E[]表示求均值。
h的概率密度函数为[23]
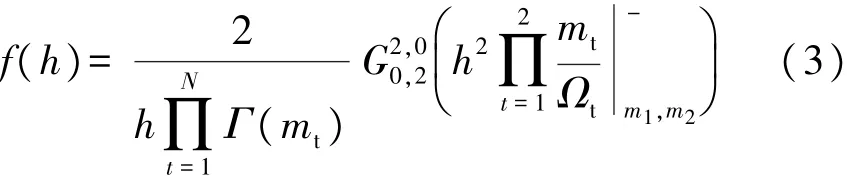
G()表示Meijer’s G函数。用位置增益QSD表示S相对于D的位置,QSE表示S相对于E的位置。在D和E处,接收信号分别为

式中:x表示发射信号,nSDi,nSEi为加性复高斯噪声。nSDi,nSEi的均值和方差分别为0和N0/2。E表示 x的发射功率。
D的接收信噪比表示为平均接收信噪比为


式中:K为主信道相对于窃听信道的信噪比增益。
E的接收信噪比γSEi为

其平均接收信噪比为

rk(k∈{D,E})的累积分布函数表示为

γk的概率密度函数表示为
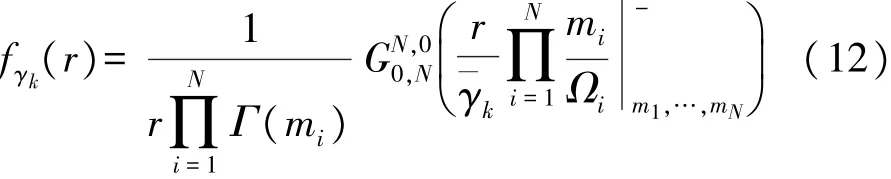
瞬时安全容量定义为[27]

对于最佳天线选择算法,我们选择发射天线w为
对于次最佳天线选择算法,我们选择发射天线g为


2 最佳天线选择算法的安全中断概率
最佳天线选择算法的安全中断概率SOP为[28]

式中:γth是给定的目标安全容量门限值。
V1可以表示为
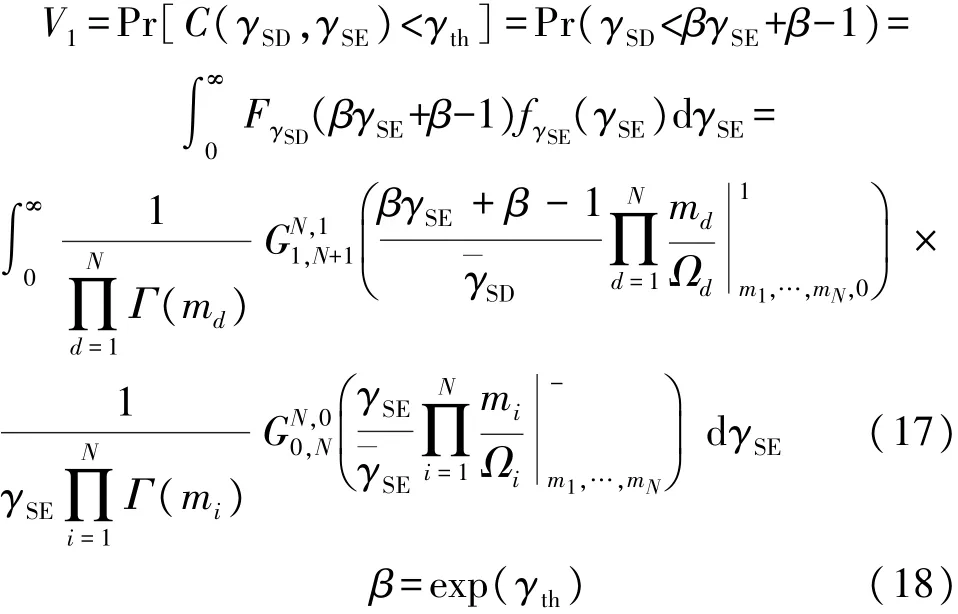
3 次最佳天线选择算法安全中断概率
次最佳天线选择算法的安全中断概率SOP表示为

4 安全中断概率的下界
在式(17)中,含有复杂的函数,我们得不到闭式解。本文利用文献[28]中的方法,推导了最佳天线选择算法的安全中断概率下界的闭合表达式。其下界的闭合表达式为

5 数值仿真
在 2-Nakagami信道下,E=1,¯γ=10 dB。
在图2、图3中,分别分析了两种天线选择算法的SOP性能。仿真系数如表1所示。理论值是按照式(16)、式(19)计算得到的。由图2、图3可知,Monte-Carlo仿真值与理论值拟合的很好,理论值的正确性得到了验证。当发射天线数Nt一定时,系统的SOP性能随着K的增大而不断改善,这是因为移动合法目的端D节点的通信质量比移动窃听者E节点更好;当K的取值一定,随着Nt的增大,系统的通信信道状况越来越好,系统的SOP性能是不断改善的。

图2 最佳天线选择算法的SOP性能

图3 次佳天线选择算法的SOP性能

表1 仿真系数
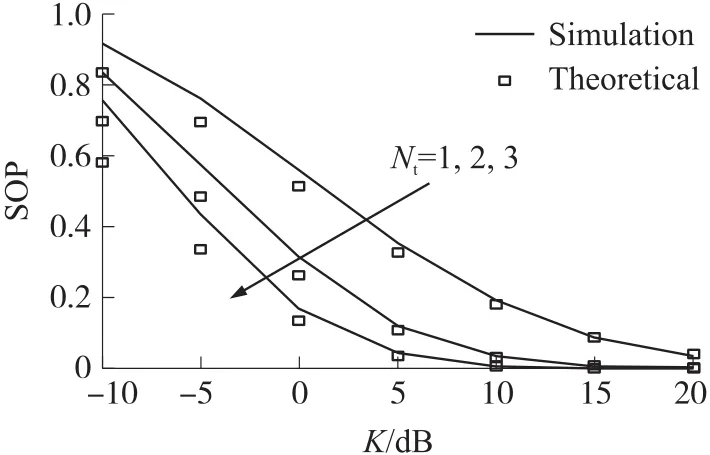
图4 最佳天线选择算法的SOP性能下界
在图4中,分析了最佳天线选择算法的SOP性能的下界。仿真系数如表2所示。由图4可知,当发射天线数Nt一定时,增大K的取值,移动合法目的端D节点的通信质量比移动窃听者E节点更好,Monte-Carlo仿真值不断的接近下界理论值。当K大于0 dB时,Monte-Carlo仿真值与理论值拟合的很好,理论值的正确性得到了验证。当K的取值一定,随着Nt的增大,系统的通信信道状况越来越好,系统的SOP性能是不断改善的。

表2 仿真系数
图5分析了位置增益(QSD,QSE)对无线传感器通信系统的SOP性能的影响。仿真系数如表3所示。由图5可知,当(QSD,QSE)一定时,增大K的取值,可以不断改善系统的SOP性能。当K的取值一定,(QSD,QSE)= (5 dB,1 dB)时,系统的 SOP 性能是最佳的,这是因为移动合法目的端D节点比移动窃听者E节点更加接近移动信源S节点,合法目的端的通信质量也越好。

图5 (GSD,GSE)对SOP性能的影响

表3 仿真系数

图6 m对SOP性能的影响
图6 分析了衰弱系数m对无线传感器通信系统的SOP性能的影响。仿真系数如表4所示。衰弱系数m的不同,代表了衰弱信道的不同。当m=2,3时,信道是2-Nakagami信道;当m=1时,信道就简化成了2-Rayleigh信道。由图6可知,当K逐渐增大时,m越大,信道的衰弱程度越小,通信质量越好。所以K越大,m越大,系统的SOP性能越好。当m固定时,增大K可以改善SOP性能。
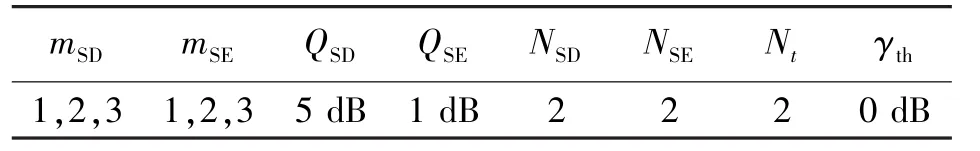
表4 仿真系数
在图7中,我们分析了不同天线选择算法对无线传感器通信系统的SOP性能的影响。在这里,分别使用了随机选择算法,Doolittle-QR选择算法[29],最佳天线选择算法和次最佳天线选择算法。仿真系数如表5所示。

图7 不同天线选择算法对SOP性能的影响

表5 仿真系数
由图7可知,对于不同的天线选择算法,增大K的取值,移动合法目的端D节点的通信质量比移动窃听者E节点更好,可以不断改善系统的SOP性能。当K的取值一定时,最佳天线选择算法的SOP性能是最佳的。随着K的增大,系统的通信信道状况越来越好,不同天线选择算法的SOP性能的差距是不断减小的。
6 结束语
本文在2-Nakagami信道下,研究了无线传感器通信系统的物理层安全性能。基于Wyner窃听模型,分别推导了最佳天线选择算法和次最佳天线选择算法的SOP的精确表达式。对于最佳天线选择算法,我们又推导了其SOP下界的闭合表达式。然后在不同条件下,通过Monte-Carlo仿真,对系统的安全性能做了验证分析。同时,我们通过优化位置增益(QSD,QSE)或发射天线Nt,可以改善系统的SOP性能。
