改进蚁狮算法的无线传感器网络覆盖优化∗
2019-03-26徐钦帅魏康园
徐钦帅,何 庆∗,魏康园
(1.贵州大学大数据与信息工程学院,贵阳550025;2.贵州大学贵州省公共大数据重点实验室,贵阳550025)
无线传感器网络WSN(Wireless Sensor Network)是一种自组织网络,由能够进行传感、处理和无线通信的传感器节点组成[1]。网络区域覆盖是WSN中的一个关键问题,对传感器节点的覆盖分布进行优化,能够改善网络的服务质量和能耗平衡。
近年来,群体智能算法被广泛应用于WSN传感器节点覆盖优化问题中,如周海鹏等[2]提出了一种动态自适应混沌量子粒子群算法,对比其他改进粒子群算法的覆盖率有所提高,但其精度及节点均匀度不够理想;胡小平等[3]基于多种策略改进灰狼优化算法用于节点覆盖优化,覆盖率和收敛速度均优于基本灰狼优化算法,但其优化结果与其他算法相比并不具备优势;李光辉等[4]提出了一种结合Voronoi图、虚拟力扰动和布谷鸟搜索算法的网络覆盖优化算法,有效提高了覆盖率;付光杰等[5]借鉴贝叶斯预测算法思想改进人工蜂群算法,取得了较好的覆盖效果,但要实现近似完全覆盖仍需改善。上述研究成果表明,多种不同群体智能算法应用于WSN网络覆盖优化行之有效,但优化效果仍有待提高。
蚁狮优化算法ALO(Ant Lion Optimizer)是一种新的群体智能优化算法,由澳大利亚学者Seyedali于2015年提出[6]。由于其初始参数少和收敛精度高的优点,已被广泛应用于WSN数据收集[7]、天线阵列合成[8]、光伏参数寻优[9]和无人机航径规划[10]等多种工程领域。研究证明[6]ALO算法的寻优性能优于粒子群算法、遗传算法和布谷鸟搜索算法等7种智能算法。因此,将ALO算法应用于WSN覆盖优化值得深入探索。然而,与其他智能算法相似,ALO算法具有早熟收敛、易陷入局部最优等缺点。对此,国内外许多学者对其进行了改进,如Dinkar等[11]引入反向学习机制,并利用拉普拉斯分布代替正态分布,扩大了算法搜索范围;Yao等[12]采用莱维飞行的不均匀步长作为蚂蚁游走步长,基于1/5原理动态调整蚁狮陷阱,改善了算法的收敛性能;张振兴等[13]使用Tent映射初始化种群位置并引导蚂蚁游走,采用锦标赛选择策略,形成全局与局部并行搜索模式,提高了算法的寻优效率。尽管改进算法各有优势,但如何使算法能够跳出局部最优、提升收敛速度,以及如何实现全局探索与局部开发能力的平衡仍是难点。
为了实现WSN覆盖率的最大化,针对ALO算法的缺陷,本文提出一种基于连续性边界收缩因子、位置更新动态权重系数和动态混合变异策略的改进蚁狮算法MS-ALO(Mixed Strategy based Ant Lion Optimizer),应用于WSN传感器节点覆盖优化。仿真实验首先通过对基准函数的优化对比,验证改进策略的有效性;然后将MS-ALO算法应用于WSN覆盖优化问题,选取不同文献中4种算法在相同条件下进行对比实验,验证该算法的应用价值。
1 问题模型分析
假设在面积为S=L1×L2的二维正方形WSN监测区域内,随机部署N个同构传感器节点,节点集合定义为 Z = {z1,z2,…,zi,…,zN},zi位置坐标为(xi,yi),i= 1,2,…,N,每个节点的感知半径均为Rs,通信半径均为Rc。由于传感器节点的感知范围是一个以自身为圆心、Rs为固定半径的封闭圆形区域,为方便计算,将该监测区域离散化为m×n个待覆盖像素点,其集合为 Hj=(xj,yj),j∈{1,2,…,m×n},每个像素点的几何中心点即覆盖优化目标位置。
若像素点Hj与任意一个节点距离小于或等于感知半径Rs,则认定Hj已被网络覆盖。节点zi与像素点Hj的间距定义为

像素点Hj被传感器节点zi感知的概率p(zi,Hj)定义为

式中:Re为传感器节点的感知误差;λ为感知衰减系数。
在该区域内,任意一个像素点能同时被多个节点感知,其联合感知概率p(Z,Hj)定义为

该区域的覆盖率Rcov为节点集合Z所覆盖的像素点总数与区域内像素点总数的比值,定义为

因此,将式(4)作为文中改进蚁狮算法求解WSN覆盖优化问题的目标函数,即所有位置变量在监测区域范围内,利用改进算法优化求解覆盖率Rcov的最大值。
2 蚁狮优化算法基本原理
ALO算法原理源于自然界中蚁狮猎食蚂蚁行为的启发,描述如下:
随机初始化种群位置,计算适应度值,并采用轮盘赌方法选择蚁狮修筑陷阱。
蚂蚁在搜索空间内随机游走,定义为

式中:cumsum为位置累计;t为当前迭代次数;T为最大迭代次数;r(t)为随机数0或1,定义为

式中:m为在[0,1]内的随机数。
同时,为了使蚂蚁的随机游走保持在搜索空间内,对其位置进行归一化处理,定义为

式中:bi和ai分别为第i个变量的上界和下界;di和ct分别为第t代时第i个变量的上界和下界。i
轮盘赌选择的蚁狮位置影响着蚂蚁的游走边界,定义为

式中:dt和ct分别为所有变量在第t代的上界和下界;Antliontj为第t代第j只蚁狮的位置。
当蚂蚁围绕陷阱随机游走时,蚁狮会继续深挖以防蚂蚁逃出,使蚂蚁游走边界逐渐缩小直至滑落陷阱底部,该过程定义为

式中:I为边界收缩因子,定义为

式中:w为由t和T决定的常数。
蚂蚁滑落到陷阱底部被蚁狮捕捉,若种群中包含适应度高于蚁狮的个体,则该个体将作为新蚁狮重筑陷阱,定义为

式中:Antliontj为第t次代第j只蚁狮的位置;Antti为第t代第i只蚂蚁位置;f为适应度函数。
选择当代最优蚁狮作为精英蚁狮,同轮盘赌选择蚁狮一起引导蚂蚁的位置更新,定义为
式中:RtA为第t代绕轮盘赌选择蚁狮的蚂蚁随机游走;RtE为第t代绕精英蚁狮的蚂蚁随机游走。
3 算法分析及混合改进策略
3.1 连续性边界收缩因子
在基本ALO算法中蚂蚁围绕陷阱游走阶段,其边界即搜索范围逐渐缩小,以开发陷阱邻域最优值。但由式(12)可知,边界收缩因子I的变化呈现间断增大趋势,其间断式增大易导致蚂蚁遗漏部分区域,使算法易错过最优值[14];而从文献[6]中ALO算法优化单峰函数Sphere和Schwefel 2.21的收敛曲线可知,虽然其收敛精度在迭代后期时优于PSO、BA和CS等算法,但由于I的间断式增大,搜索边界不均匀缓慢衰减,导致收敛速度劣于其他参比算法。
针对上述问题,为了增强算法的遍历性,使其更全面地搜索求解空间以及提高算法收敛速度,提出一种随着算法迭代进化而快速连续增大的边界收缩因子,将蚂蚁游走边界更新方式定义为

式中:γ为收缩调节系数;λ为比例因子;经过多次基准函数优化实验,选取γ=400,λ=20。
3.2 位置更新动态权重系数
在精英化阶段,蚂蚁根据式(14)学习轮盘赌选择蚁狮和精英蚁狮行为以更新位置。已知蚁狮被轮盘赌选择概率为

式中:f(xi)为个体适应度值。
由于精英蚁狮具有最优适应度值,由式(16)便有较大概率被选作轮盘赌选择蚁狮[15],导致蚂蚁只绕精英蚁狮游走,而降低算法全局探索能力,如式(17)所示:

针对上述问题,将基于迭代次数的动态权重系数引入蚂蚁位置更新式(14),改进为

在式(18)中,轮盘赌选择蚁狮RtA的权重系数k1在迭代前期较大,使蚂蚁在搜索空间内探索更优区域;而在后期,精英蚁狮邻近最优区域,其权重系数k2逐渐增大,使蚂蚁在最优区域邻域开发,以此提高算法全局探索与局部开发的平衡能力。
3.3 动态混合变异
由于游走边界的收缩和精英蚁狮引导种群聚拢,导致种群多样性减小,而易发生早熟收敛现象,陷入局部最优。
为了使算法能有效跳出局部最优,提出一种结合早熟收敛判断方法与动态混合变异的改进策略。首先,采用文献[16]中的早熟判断方法,将第t代的全局适应度方差αt定义为
式中:N为种群规模;ft(xi)为第i个个体在第t代的适应度;ft
mean为第t代全局平均适应度;fta为限定αt的标定因子,定义为


然后,将个体间距Dt定义为

式中:L为搜索空间最大对角长度;n为搜索维度;xtid为第t代时第i个个体在第d维的位置;xtmean为第t代时所有个体在第d维的位置平均值。
已知αt和Dt在种群完全聚集时将等于0,此时可能达到全局收敛或陷入局部最优。为了进一步区分,设当 αt<β 且 Dt<σ(β=10-6,σ=10-3)时,则判定算法已早熟收敛。
针对算法陷入局部最优的困境,提出一种基于正态分布和柯西分布动态调整的混合变异方法,对蚁狮位置Antliontj进行变异扰动操作,如式(22)所示:
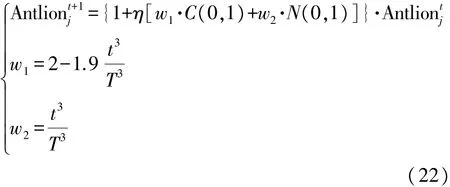
式中:Antliontj+1为第t+1代的蚁狮位置;η 为调节系数;C(0,1)为服从柯西分布的变异因子;N(0,1)为服从正态分布的变异因子。
已知柯西分布比正态分布变异尺度更大[17]。在式(20)中,柯西变异因子系数w1与k1相似的是其取值均随迭代次数递减,不同的是w1取值范围为[0 .1,2),比 k1变化幅度更大,结合 C(0,1)相对较大的变异步长,使算法能跳出局部最优,探索更广泛的区域;正态变异因子权重w2=k2,随迭代次数逐渐增大,较小的变异步长以便算法快速收敛,并在最优值邻域进行搜索。
同时,为了保证变异策略产生的新解始终朝向更优区域移动,每次操作复制M个当代蚁狮位置进行变异产生新解,最后在M+1个候选解组成的解集中选择最优解进入下一次迭代,文中所有实验取M=20。
4 覆盖优化算法设计
基于MS-ALO算法的WSN覆盖优化的目标为监测区域覆盖率Rcov的最大化;输入为MS-ALO算法的种群规模N和最大迭代次数T,以及监测区域面积S、像素点数m×n、传感器节点数V和感知半径Rs等参数;输出为Rcov最优适应度值,以及传感器节点分布坐标。
MS-ALO算法的种群中每个个体代表区域内所有节点的一个覆盖分布;寻优维度d=2 V,则节点分布坐标可表示为(2d-1,2d)。算法流程如图1所示。

图1 基于MS-ALO算法的WSN覆盖优化
具体算法步骤如下:
Step 1 输入WSN监测区域、传感器节点及MS-ALO算法相关参数;
Step 2 在搜索空间即监测区域内,随机初始化种群中的个体位置;
Step 3 初始化迭代次数t=1;
Step 4 将节点覆盖率Rcov作为目标函数,根据式(4)计算种群适应度,保存最优个体作为精英蚁狮;
Step 5 利用轮盘赌方法选择适应度较高的蚁狮挖掘陷阱;
Step 6 由式(8)和式(9)计算蚂蚁个体游走上下边界;
Step 7 蚂蚁在边界内根据式(5)和式(18)围绕轮盘赌蚁狮和精英蚁狮游走,并在爬入陷阱时,根据式(15)更新游走边界;
Step 8 计算蚂蚁适应度值,根据式(13)比较判断,更新蚁狮位置并重新挖掘陷阱;
Step 9 基于当前种群适应度值及个体位置,根据式(19)和式(21)分别计算适应度方差αt和个体间距 Dt;
Step 10 若 αt<β 且 Dt<σ,执行 Step 11;否则,跳至Step 12;
Step 11 复制M个当前最优个体位置,分别根据式(22)进行混合变异操作,并构建当前最优个体与变异个体的新解集,从中选取适应度最优的个体并保存;
Step 12 更新迭代次数t=t+1,并判断是否达到最大迭代次数,若是,结束算法并输出覆盖率最优适应度值和相应节点部署坐标位置;否则,跳至Step4循环迭代。
5 仿真实验与分析
5.1 基准函数优化性能测试
为了验证混合策略的有效性,选取12个基准函数进行数值仿真,并与基本ALO算法和文献[11]提出的改进OB-L-ALO算法进行比较。实验采用的12个基准函数的名称、数学表达式及其他参数情况如表1所示,其中:f1~f5为单峰函数;f6~f10为多峰函数;f11~f12为固定低维度下的多峰函数。

表1 基准函数
为了保证算法优化性能测试的公正性,基本ALO算法、MS-ALO算法的参数设置同文献[11]中OB-L-ALO算法参数一致:种群规模N=30,最大迭代次数T=1 000。同时,为减小随机干扰的影响,不同算法对于每个基准函数均独立运行30次,并取实验结果平均值进行比较。

表2 基准函数优化结果对比
表2记录了 ALO算法、OB-L-ALO算法[11]与MS-ALO算法在相同测试条件下,对于12个基准函数的优化结果。图2为ALO算法与MS-ALO算法对基准函数优化收敛过程对比,其中:Iteration表示迭代次数;Mean best so far表示算法运行30次的平均适应度值。
从表2和图2可以看出,MS-ALO算法较其他算法均取得了更好的收敛结果。在单峰函数优化方面,该算法对f1~f3的收敛精度较ALO算法提高了至少7个数量级,表明连续性边界收缩因子策略能改善算法的遍历性,提高算法收敛速度。

图2 优化测试函数收敛曲线对比
对于多峰函数优化问题,在30维搜索空间中,以具有大量局部极值点的非线性函数Rastrigin(f7)和Griewank(f8)为例,MS-ALO算法对其优化的平均结果较ALO算法分别提高了14和9个数量级,较OB-L-ALO算法分别提高了10和3个数量级,表明改进策略能使算法有效跳出局部最优,该算法具有良好的多峰寻优能力。
在固定低维度搜索空间的多峰函数优化中,MS-ALO算法对于函数f11寻优的平均最优值已达到其理论最优值,对于f12的优化结果较参比算法也有所提高,且均值方差更小,验证了改进算法的鲁棒性。
综上所述,MS-ALO算法对于基准函数的优化求解在收敛精度、收敛速度、多峰优化能力和鲁棒性等方面,均优于基本ALO算法及其改进算法OB-LALO,验证了混合改进策略的有效性。因此,该算法可进一步应用于WSN的节点覆盖优化问题。
5.2 WSN覆盖优化应用
5.2.1 实验设置
为了充分验证MS-ALO算法对WSN节点覆盖的优化性能,选取基本ALO算法和不同文献中4种改进算法,分别在相应监测区域对不同数量的传感器节点进行覆盖优化对比。参比文献及其算法如表3所示,仿真实验参数与相应文献参数设置相同。参比文献及算法

表3
5.2.2 与DACQPSO算法对比
实验参数设置与文献[2]相同,如表4所示。

表4 参数设置
为了降低随机性对实验结果的干扰,利用ALO算法和MS-ALO算法对该区域进行20次优化,取平均覆盖率对比。表5给出了ALO算法、MS-ALO算法与DACQPSO算法平均覆盖率优化结果对比。图3和图4分别为ALO算法和MS-ALO算法优化后该区域节点分布图和收敛曲线图。

表5 覆盖率优化结果对比

图3 优化后节点分布

图4 覆盖优化收敛曲线
由表5可知,在相同测试条件下,MS-ALO算法运行20次优化的平均覆盖率相比DACQPSO算法和基本ALO算法分别提高了6.31%和7.07%,较大程度地提高了网络覆盖率。同时,从图3可以看出,基本ALO算法覆盖优化效果较差,MS-ALO算法优化后节点分布更加均匀,无线网络覆盖范围更加广泛,且改善了文献[2]中DACQPSO算法优化节点分布区域边界覆盖盲区较大的问题。
另一方面,已知文献[2]中DACQPSO算法的迭代次数为150,取得了87.15%的网络覆盖率。而由图4可知,MS-ALO算法和基本ALO算法在150代取得的平均覆盖率分别为88.11%和82.97%,可知MS-ALO算法相比DACQPSO算法和ALO算法的覆盖率分别提高了0.96%和5.14%,说明位置更新动态权重系数等改进策略的引入提升了算法在迭代前期的全局搜索能力,有效地提高了相同迭代次数下的网络覆盖率。同时,从图4可以看出,由于连续性边界收缩因子的改进,MS-ALO算法在380代开始收敛,相比ALO算法提前了430代,提高收敛精度的同时,明显加快了收敛速度。
5.2.3 与IGWO算法对比
参数设置与文献[3]相同,如表6所示。
利用MS-ALO算法对该区域进行20次覆盖优化,取平均覆盖率对比。表7给出了ALO算法、MSALO算法与IGWO算法平均覆盖率优化结果对比。图5和图6分别为ALO算法和MS-ALO算法优化后该区域节点分布图和收敛曲线图。

表7 覆盖率优化结果对比
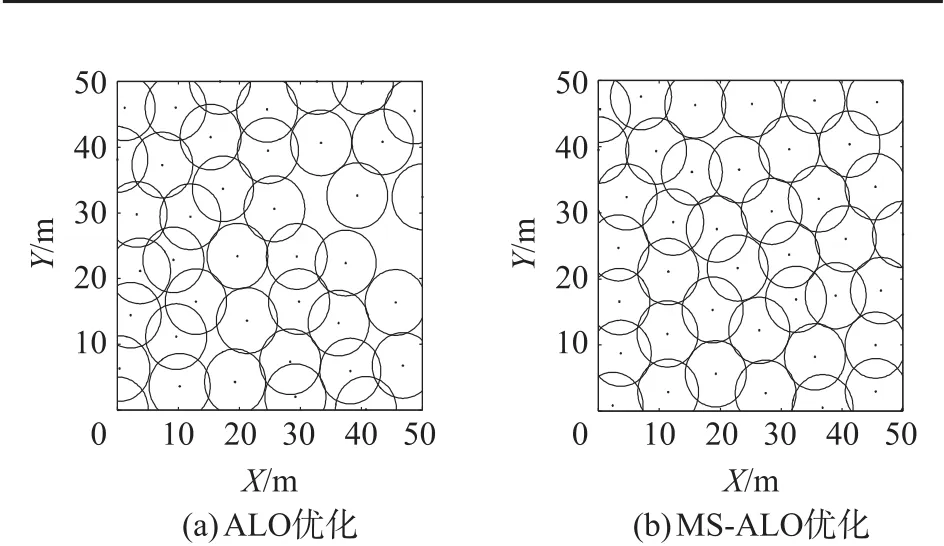
图5 优化后节点分布

图6 覆盖优化收敛曲线
由表7可知,MS-ALO算法进行20次覆盖优化的平均覆盖率相比IGWO算法和ALO算法分别提高了2.17%和5.38%。在图3所示节点分布中,ALO算法优化后区域节点覆盖盲区较大,MS-ALO算法优化后节点分布更加均匀,改善了文献[3]中IGWO算法节点区域聚集现象。
在收敛速度方面,已知文献[3]中IGWO算法在100代时已经收敛,而由图4可知,MS-ALO算法在100代时平均覆盖率为91.52%,相比IGWO算法降低了2.76%,且在550代时收敛。虽然本文算法的收敛速度差于IGWO算法,但由于改进的边界收缩因子随着算法迭代进化而快速连续增大,从图4可以看出,本文算法相比基本ALO算法提前了300代收敛,收敛速度有了较大提升。
5.2.4 与VF-CS算法对比
参数设置与文献[4]相同,如表8所示。

表8 参数设置
利用MS-ALO算法对该区域进行30次优化,取平均覆盖率对比。表9为ALO算法、MS-ALO算法与VF-CS算法对不同传感器节点数量的平均覆盖优化结果对比。图7和图8分别给出了ALO算法和MS-ALO算法优化后该区域内传感器节点数为90和80的节点分布图,图9为相应收敛曲线。

表9 覆盖优化结果对比
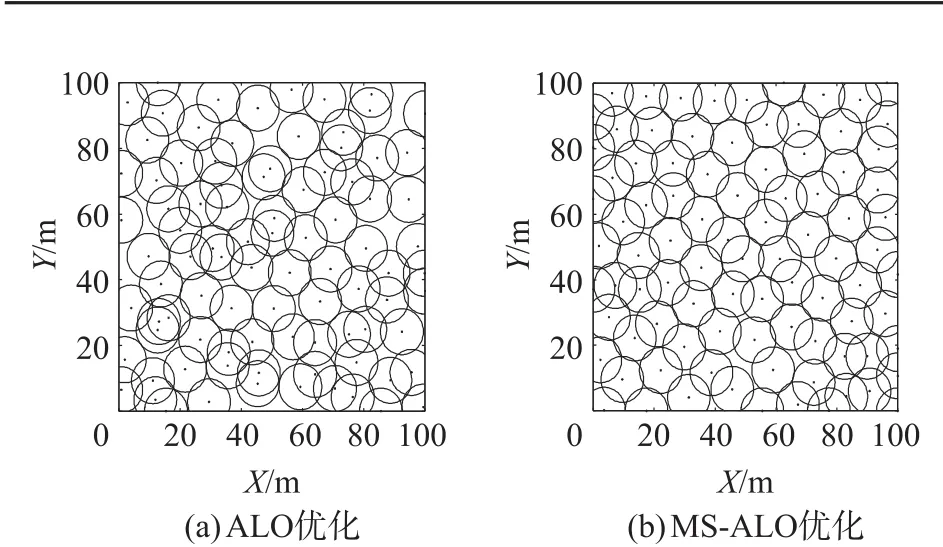
图7 V=90时优化后节点分布

图8 V=80时优化后节点分布
由表9可知,在相同的监测区域,随着部署节点数的增加,覆盖率也在逐渐提高。在节点数为80、70、50和40时,MS-ALO算法优化的平均覆盖率相比于VF-CS算法分别提高了0.11%、1.37%、0.27%和1.43%;而在节点数为90和60时,则比VF-CS算法分别降低了0.09%和1.88%。相比于基本ALO算法,MS-ALO算法对不同数量节点优化的平均覆盖率则分别提高了8.68%、7.82%、14.2%、7.72%、8.88%和8.15%,表明动态权重系数的引入能够有效平衡算法的全局与局部搜索能力,从而有效提高算法的收敛精度。

图9 覆盖优化收敛曲线
同时,以节点数为90和80为例,从图7和图8可以看出,MS-ALO算法相比ALO算法更好地实现了区域节点部署优化。在收敛速度方面,已知文献[4]中VF-CS算法仅用50次迭代便实现了收敛。从图9可以看出,MS-ALO算法对于节点数为90和80的覆盖优化实验中,分别在695代和700代收敛,而ALO算法则分别迭代至935代和950代开始收敛。因此,MS-ALO算法的收敛速度虽差于VFCS算法,但相比基本ALO算法仍有很大地提高。
5.2.5 与BPABC算法对比
参数设置与文献[5]相同,如表10所示。

表10 参数设置
利用MS-ALO算法对该区域进行200次覆盖优化,取平均覆盖率对比。表11为ALO算法、MSALO算法与BPABC算法的平均覆盖率和最差覆盖率数值对比。图10和图11分别为ALO算法和MSALO算法优化后节点分布图和相应收敛曲线图。

表11 覆盖率优化结果对比
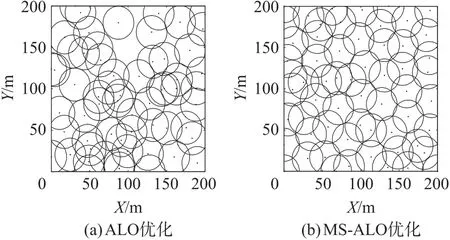
图10 优化后节点分布

图11 覆盖优化收敛曲线
由表11可知,MS-ALO算法运行200次优化的平均覆盖率相比BPABC算法和ALO算法分别提高了2.02%和8.49%,最差覆盖率相比两种算法分别提高了3.13%和10.23%,收敛精度和稳定性均有较大程度地提高。在如图10所示的节点分布中,基本ALO算法优化后传感器节点在部分区域过于聚集,覆盖盲区较大;而MS-ALO算法优化后节点分布较均匀,有效缩减了无线网络盲区,近似实现了区域完全覆盖。
另外,从图11可以看出,MS-ALO算法迭代至500代时已接近收敛,但由于早熟收敛判断机制的引入,使得算法利用动态混合变异策略跳出局部极值,以搜索更优解,进一步提高了收敛精度。如图11所示,MS-ALO算法和ALO算法分别在615代和790代时收敛,说明改进策略有效提升了MS-ALO算法的收敛速度,能够更快速地寻优最大覆盖率。
综上所述,通过与不同算法在相应同等测试条件下的实验结果对比,MS-ALO算法实现了更高的平均覆盖率、较均匀的传感器节点分布和较少的网络覆盖盲点,验证了该算法具有较好的WSN覆盖优化性能。
6 结束语
针对无线传感器网络覆盖率最大化的目标,本文提出了一种基于混合策略的改进蚁狮优化算法(MS-ALO)实现传感器节点的覆盖优化。该算法通过连续性边界收缩因子,提高了算法对搜索空间的遍历性和收敛速度;利用位置更新动态权重系数,增强了算法的全局探索与局部开发的平衡能力;基于早熟收敛判断和动态混合变异机制,改善了算法易陷入局部最优的问题。通过对不同形态基准函数的优化求解,以及与基本蚁狮优化算法和其改进算法的对比,验证了改进策略的有效性。
将MS-ALO算法进一步应用于无线传感器网络覆盖优化,选取基本ALO算法和不同参考文献中4种覆盖优化算法,在相同测试条件下进行对比实验。实验结果表明,基于MS-ALO的WSN覆盖优化算法多次运行取得的平均覆盖率,除了与文献[4]在传感器节点数为90和60对比时略低于VF-CS算法0.09%和1.88%,对于其他参比算法均有较大程度的提升;同时,通过与ALO算法和参比文献中的传感器节点优化分布图对比,MS-ALO算法优化后的节点分布更加均匀,覆盖盲区更小;然后,通过对比覆盖优化收敛曲线,验证了改进策略对于ALO算法收敛速度的有效提升。因此,本文算法能够较好地提高无线传感器网络的性能。然而,如何在保证较高覆盖率收敛精度的情况下进一步提升算法收敛速度,是MS-ALO算法下一步需要完善的工作。
