基于非局部均值算法的图像去噪方法研究

2019-03-26钱海明孙金彦王春林

安徽水利水电职业技术学院学报 2019年1期

钱海明，孙金彦，王春林

(1.安徽省·水利部淮河水利委员会水利科学研究院,安徽合肥 230088；2.水利水资源安徽省重点实验室，安徽合肥 230088;3.安徽省大禹水利工程科技有限公司，安徽合肥 230088)

图像在采集、传输和加工等过程中，由于受外界环境影响，存在一定的噪声，导致图像质量严重下降。图像去噪作为图像恢复的重要手段之一，被广泛应用到图像处理领域。图像中的噪声问题，可近似看成呈高斯分布的白噪声，进而去除高斯白噪声成为了一个重要方向。为了进一步抑制噪声，为后续处理提供更为真实的信息。诸多学者提出很多的模型及方法。本文利用非局部均值算法去除图像中的噪声问题，通过图像中的冗余信息进行加权平均，将使像素点去噪后的灰度值用与点的高斯邻域相似的灰度值的平均代替，增强了图像去噪的效果。

1 非局部图像去噪算法

1.1 非局部平均算法

假设噪声信号为与图像无关的高斯白噪声，噪声模型为：

V(i)=X(i)+N(i)

(1)

其中，X(i)表示未受噪声污染的原始图像；N(i)表示均值为0，方差为σ^2的白噪声；N(i)表示受污染的噪声图像。对于一幅给定的离散含噪图像v={v(α)|α∈I}，非局部平均的方法利用整幅图像中所有像素灰度值加权平均来得到该点的灰度估计值，即

NL[v](α)=∑β=1ω(α,β)v(β)

(2)

其中，权值ω(α,β)表示依赖于α与β之间的相似性，并满足条件：0≤ω(α,β)≤1，∑ω(α,β)=1。像素α与β的相似性由与之相对应的灰度值向量v(Nα)与v(Nβ)之间的相似性决定,Nk表示以像素k为中心的固定大小的方形领域,如v(Nk)由领域Nk内的灰度值组成的向量。图1中的3个像素点α、β1与β2，分别用小白点表示。以这3个像素为中心的方形领域分别Nα、Nβ1)与Nβ2)，白色方框表示，由这3个方形领域内的灰度值组成的向量分别记为v(Nα)，v(Nβ1)和v(Nβ2)。设α为当前待处理的像素，则像素α与像素β1与β2的相似性由v(Nα)和v(Nβ1)以及v(Nα)和v(Nβ2)的相似性决定。显然像素α与像素β1具有相似的领域，与像素β2的领域差异较大，所以对于像素α的去噪，像素β1的贡献要比像素β2的大些。

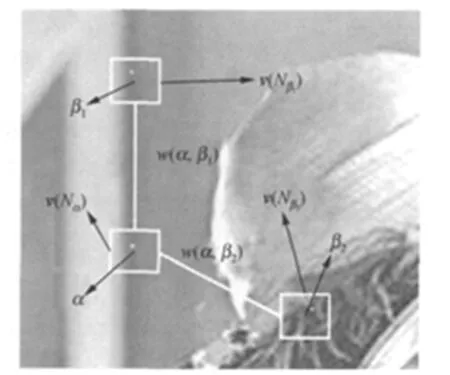
图1 图像自相似性示例

(3)

其中，Z(α)表示归一化常数。

非局部平均的方法建立在对图像反映领域相似性的权值进行计算的基础之上，图像中每一个像素点的领域要与图像中所以像素点的领域进行一一比较，计算量非常大。对于一副大小为NxN的图像，领域大小为dxd，则算法的复杂度为O(N4d2).

1.2 参数的选择

在非均值算法中，采用与噪声标准差线性正比关系确定滤波参数h，即h=10σ。研究分析得到h与噪声方差σ2有近似线性正比关系，且受到噪声图像方差的影响。因此，在去噪过程中，存在3个参数可以控制去噪效果，分别是滤波参数h、领域窗口半径Rsim以及非局部大小的搜索窗口半径Rwin。权值函数ω(i,j)中的参数h控制了指函数的衰减来控制权值的大小从而控制平滑噪声的程度。若参数h较小，则幂函数的衰减效果比较显著，细节保留程度较高。一般情况下，图像中包含方差σ^2的白噪声，参数h的取值为10σ～15σ。领域窗口半径Rsim用来比较两个像素的相似程度的空间邻域的半径。本文选取的窗口大小半径为2，领域窗口大小为5×5。由于单个计算所有像素的权值的计算量比较大，为了增加计算速度则应该确定一个邻域来计算所有邻域内像素的加权平均。在本文中的Rwin的取值为5，即搜寻窗口大小为11×11。