基于ANSYS的海上风机重力式基础载荷施加形式研究

2019-03-26田会元许洪露

水电与新能源 2019年3期

田会元，许洪露

(中国长江三峡集团上海勘测设计研究院有限公司，上海 200434)

能源是人类生存的基础，在煤炭、石油、天然气等化石能源的推动下，人类经济社会活动发展迅速[1]。但是，在社会经济快速发展的同时，人类也面临着资源枯竭、环境恶化等严峻挑战，开发绿色清洁能源，调整能源产业结构已刻不容缓。占地球面积71%的海洋蕴藏着巨大的能量，包含着风能、波浪能、潮流能、潮汐能等多种能源[2]。与其他海洋可再生能源相比，风能的开发与利用已逐渐趋于产业化、规模化。海洋环境载荷复杂，对风机基础的承载能力及耐久性要求较高。因此，基础结构的安全、稳定与成本成为制约海上风电发展的关键因素。

目前，海洋风机基础形式主要有单桩基础、高桩承台基础、重力式基础、吸力筒式基础以及导管架基础等类型，其中运用最多的是桩基础和重力式基础。重力式基础由钢筋混凝土或钢质基础结构作为基座坐立于海床面上，通过过渡段或竖井顶法兰与塔筒连接，一般适用于5～30 m水深。重力式基础具有设计简单、造价低廉，受海床沙砾影响不大，抗风暴和风浪袭击性能好等优点，近年来在工程领域应用广泛。图1为重力式基础的发展历程，第一代借鉴陆上重力式扩展基础，第二代采用配重压载的混凝土沉箱结构，第三代采用预应力混凝土结构，重力式风机基础逐渐由浅水海域向风资源更丰富的深水海域发展[3]。但深水海域、大容量风机伴随着更恶劣的海洋波浪载荷，对重力式基础结构稳定性带来巨大考验。

目前，海上重力式基础结构研究大多集中在地基承载力领域，单独针对风机载荷对结构受力特性影响的研究较少，对风机载荷施加形式的研究更为缺乏。针对上述问题，本文提出了三种风机载荷施加的方法，并从理论上剖析了三种施加方法的差异性，最后基于ANSYS有限元软件对比分析了不同载荷施加形式对重力式基础受力特性的影响，以期为海上风机重力式基础结构设计提供参考。

图1 海上风机重力式基础发展历程

1 风机载荷施加方式

风机载荷作为海洋风电基础的主控载荷，施加形式将直接影响到结构的安全性，目前对风机基础进行有限元分析时，风机载荷的施加形式多样，主要施加方式有：①将风机载荷均匀的施加在塔筒节点上；②基于ANSYS-MPC184刚性杆单元。设计者对于ANSYS-MPC184单元载荷传递特性并不是很清楚，只能作为一个实现载荷施加的黑匣子工具，而将风机载荷均匀施加在塔架节点上，从材料力学理论出发，弯矩均分与结构受力特性不符，基于以上现状，本文从材料力学薄壁圆壳与梁的纯弯曲理论出发，将风机载荷的弯矩和扭矩转换为薄壁圆壳的正应力和切应力，在满足结构实际受力特性的情况下，运用原始理论将载荷施加透明化，以期为海上风机基础结构设计提供有益参考。

1.1 载荷均布施加

风机载荷的施加较为简单的方式是先求出顶部塔筒壁上的节点数，将风机载荷值(弯矩、扭矩、水平力、竖向力)除以节点数，均匀的施加在所有节点上，如图2所示。将弯矩和扭矩均匀施加在所有节点上，与薄壁圆壳受力特性存在较大差异，圆壳上各节点受到弯矩和扭矩作用时载荷大小与节点所在的位置有关，简单将载荷均匀施加到各节点上会导致结构受力偏小(第三节中将阐述受力偏小的原因)，增加了设计的风险性。

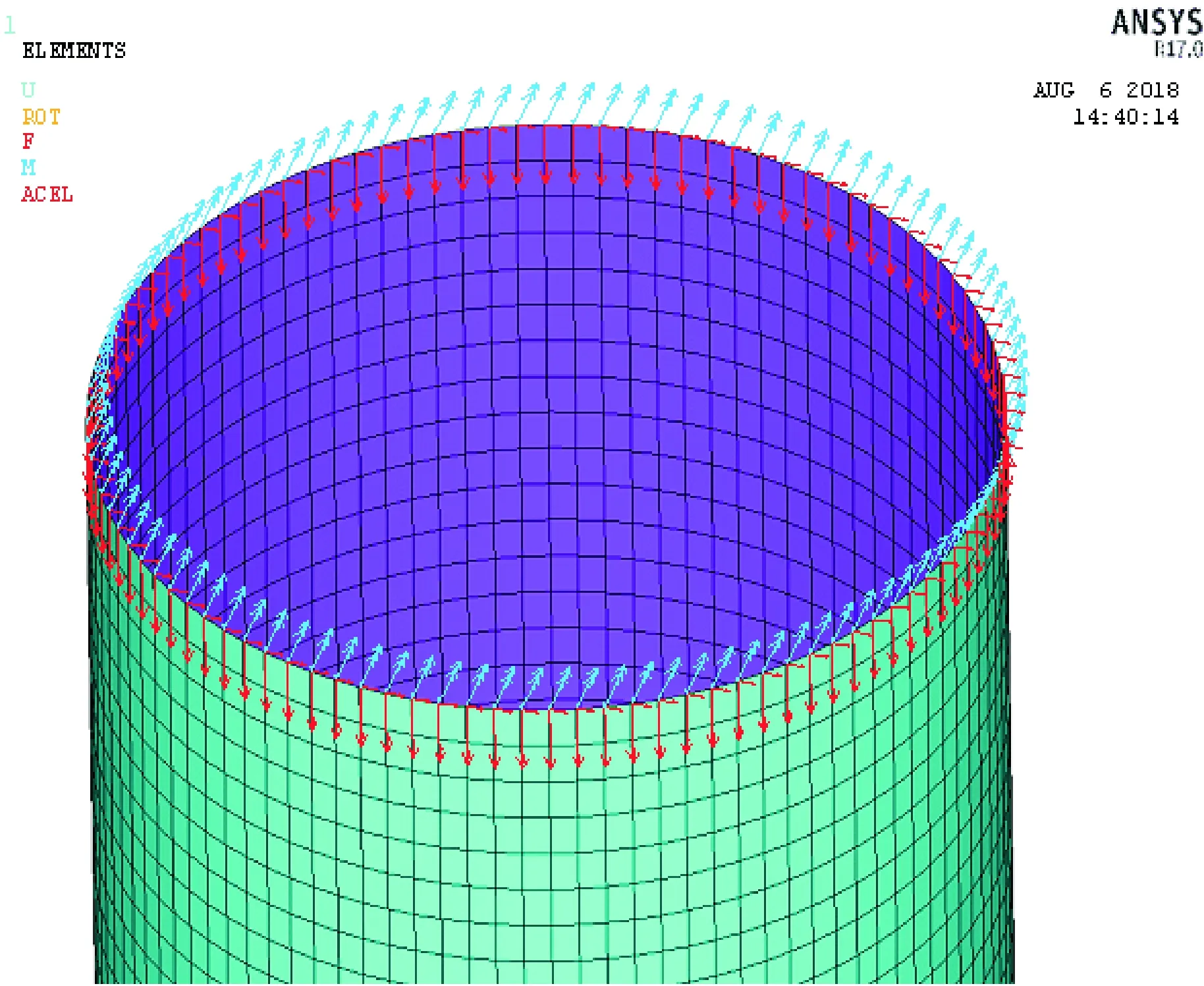
图2 风机载荷均匀施加方式示意图

1.2 基于ANSYS-MPC184刚性杆单元

MPC184称为多点约束单元(Multipoint Constraint Element)，它包含了实现节点间运动约束的一类常规多点约束单元，这些单元可简单地分为“约束类单元”或“连接类单元”。运动约束可采用两种算法，即直接消除法和拉格朗日乘子法。直接消除法通过内部生成约束方程实现，在结构总平衡方程中直接除去从节点的自由度；拉格朗日乘子法通过拉格朗日乘子实现，此法在结构总平衡方程中保留所有节点的自由度[4]。

在塔筒顶部中心处建立节点A，与塔筒壁上各节点相连组成MPC单元，如图3所示，将风机载荷值集中施加在中心点A处，运用与塔筒壁相连的MPC单元将风机载荷传递给基础结构。这类载荷施加方法是目前有限元计算学者采用较多的方式。

图3 MPC单元风机载荷施加方式示意图

1.3 基于材料力学薄壁圆壳扭转与梁横截面纯弯曲理论

1)薄壁圆壳扭转理论。薄壁圆壳扭转时，横截面上任一点处的切应力均相等，其方向与圆周相切[5]。扭矩在横截面上任意一点处切应力为

(1)

式中：τ为薄壁圆壳横截面上的切应力；Mz为扭矩；A为薄壁圆壳横截面积；R为薄壁圆壳半径。

扭矩Mz和Fz在塔筒任意一点产生的fx和fy表达式如下：

式中：N为塔筒横截面的节点数；θ为x轴和截面节点的夹角；Fx为风机水平载荷。

2)纯弯曲时梁横截面上的正应力理论。等值梁在纯弯曲时横截面上任一点处正应力为

式中：σ为横截面上的正应力；My为风机弯矩载荷；x为横截面节点水平坐标；Iz为横截面对中性轴的惯性矩；δ为塔筒壁厚。

扭矩My和Fz在塔筒任意一点产生的fz表达式如下:

2 风机载荷施加方式对比分析

三种风机载荷施加方式(图4、图5)对应的基础结构等效应力云图如图6～图8所示，由图可知，三种载荷施加方式对应的最大等效应力均出现在重力式基础圆弧过渡段，但最大等效应力值不同，表1为不同施加方式对应的风机基础结构第一、三主应力和等效应力值。

图4 风机载荷x和y方向施加示意图

图5 风机载荷z方向施加示意图

由表1可知，基于材料力学理论施加方式对应的第一主应力、第三主应力和等效应力均较大，基于MPC单元施加方式对应的第一主应力最小，均布载荷施加方式对应的第三主应力最小。

风机水平载荷和风机弯矩都会使迎风面结构受拉，背风面结构受压，均布载荷施加的方式将弯矩均匀施加在塔筒节点上，没有考虑弯矩会引起塔筒节点应力方向的变化，即迎风面产生拉应力，背风面产生压应力，而基于材料力学理论的施加方式，考虑了风机水平载荷和风机弯矩的叠加效果，更加接近基础结构真实受力状态，计算结果也更保守。

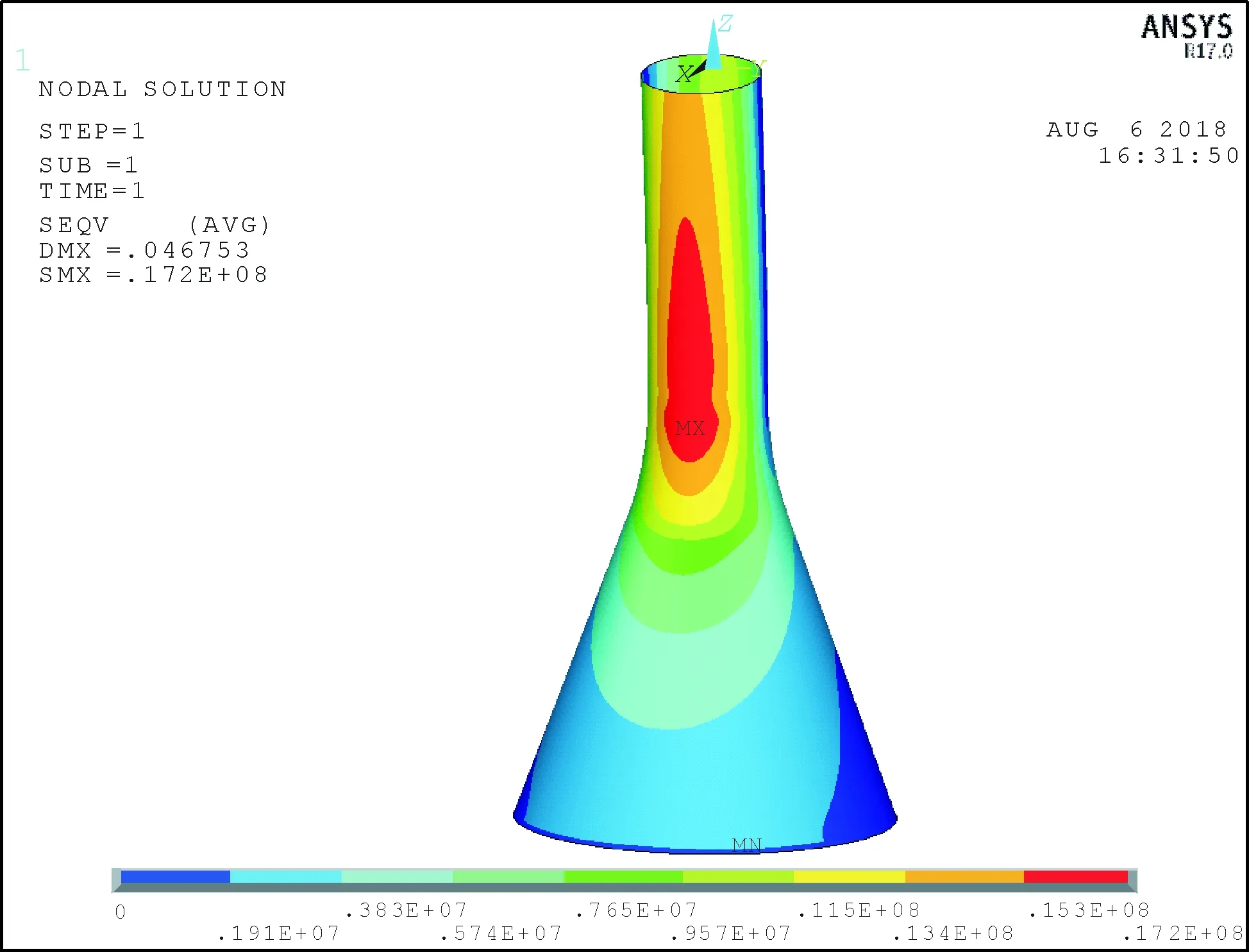
图6 均布施加方式基础结构等效应力云图

图7 MPC单元施加方式结构等效应力云图

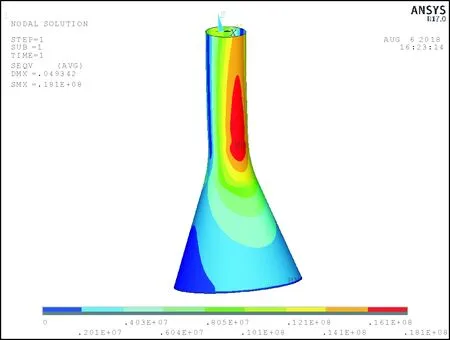
图8 材料力学理论施加方式结构等效应力云图

表1 不同施加方式对应的基础结构应力值MPa

采用MPC单元施加方式，由表1可知，对应的第一主应力(拉应力)较其余两种方式偏小，重力式基础的主体材料为混凝土，其抗拉强度远小于抗压强度，抗拉强度不足将会引起重力式基础产生裂缝，结构的抗疲劳和耐久性会大幅度下降，故重力式基础的拉应力是结构设计中的重要强度指标，若有限元分析时，计算的第一主应力偏小，对于结构设计者而言过于冒进。实际工程中会采用预应力钢筋使基础全截面处于受压状态，以此降低基础承受的拉应力。