巧用隐形圆解决线段的最值问题

◆张洁彬

(唐山市第十二中学)

求线段长的最值问题是近年来中考常见题型，解决此类问题，学生可以在教师的引导下抽象或提炼出相应的解题基本模型，从而达到提升学生的解题能力。笔者现对题目中蕴含隐形圆的基本模型做以下三点分析。

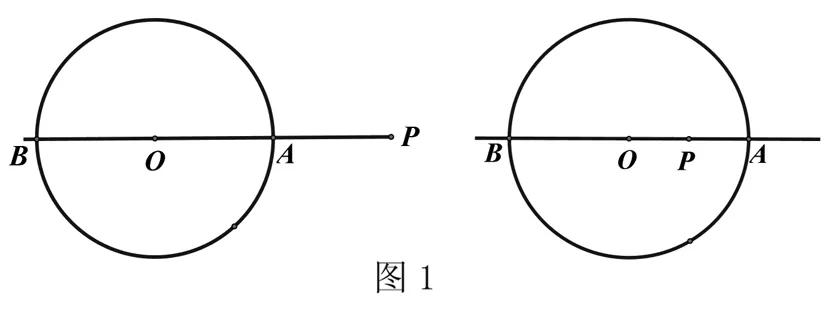
利用隐形圆求线段最值问题，要清楚解题的基本模型，利用“三角形两边之和大于第三边；三角形两边之差小于第三边。”的性质求线段的最大和最小值。如图1，当点P为⊙O外一点时，点P到圆上各点的最大距离是直线PO上点P与远交点B之间的线段PB的长，最小距离是直线PO上点P与近交点A之间的线段PA的长；当点P为⊙O内一点时，点P到圆上各点的最大距离也是直线PO上点P与远交点B之间的线段PB的长，最小距离也是直线PO上点P与近交点A之间的线段PA的长。明确模型后，就可以将“两点间线段的长”转化为“定点到圆上各点的距离”，从而通过找到动点运动轨迹是圆(弧)，利用隐形圆与远近交点的关系即“圆内(外)一点到圆上各点的连线中，点与过圆心的直线与圆近交点距离最短，远交点距离最长”来求线段长的最大和最小值。

一、“一中同长”发现隐形圆求最值

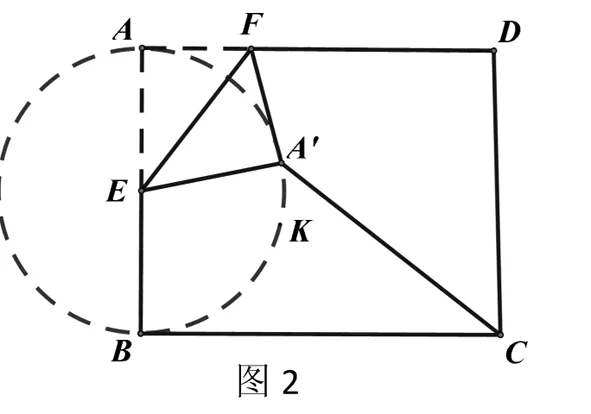
例1.如图2，在矩形纸片ABCD中，AB=2，AD=3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A’EF，则A’C的长的最小值是___.

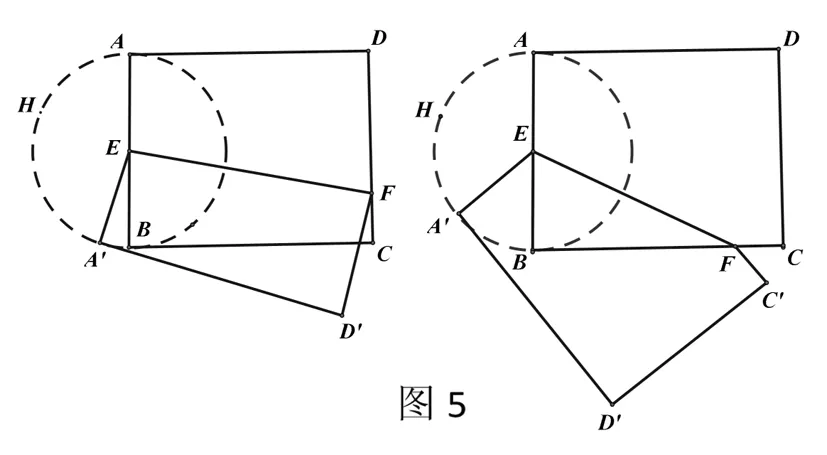
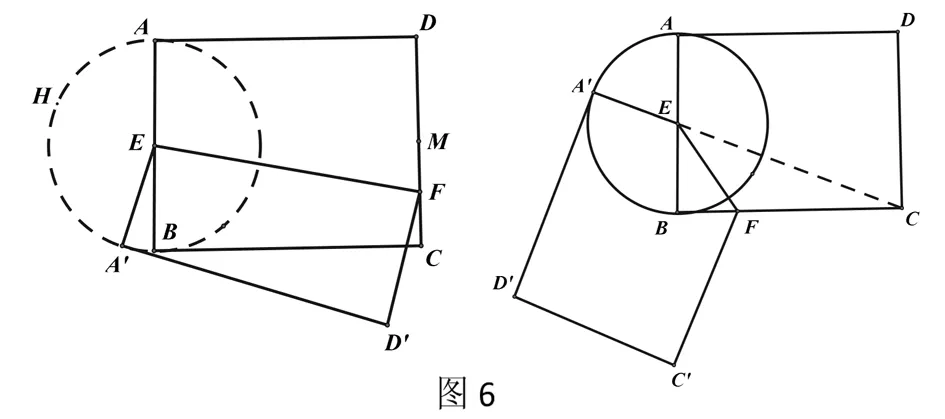
变式：如图5，在矩形纸片ABCD 中，AB=2，AD=3，点E是AB的中点，点F是AD、DC或BC边上的一个动点，将四边形ADFE或五边形ADCFE沿EF所在直线翻折，得到四边形A′EFD’或五边形A′EFC’D’，则A’C的长的最大值是___.

二、利用旋转轨迹发现隐形圆求最值

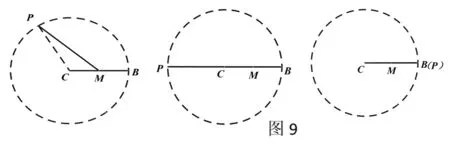
例2.如图7，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，P是A′B′的中点，连接PM，若BC=2，∠BAC=30°，求线段PM的最小值与最大值。

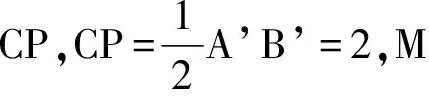
三、定弦对定角”发现隐形圆(弧)求最值

1.角为直角

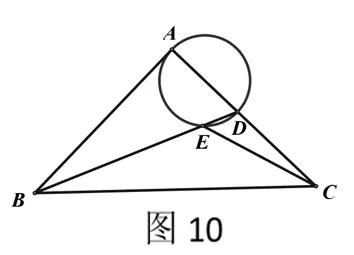
例3.如图10，在等腰Rt△ABC中，∠BAC=90°，AB=AC=2，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值为多少？

2.角为非直角

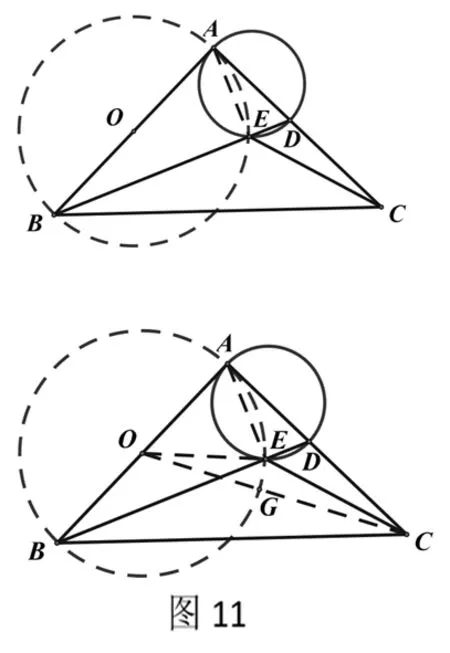
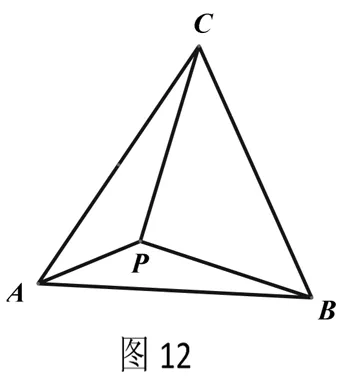
例4.如图12，△ABC为等边三角形，AB=2.若P为△ABC内一动点，且满足∠PAB=∠ACP，则线段PB长度的最小值为___.

分析：

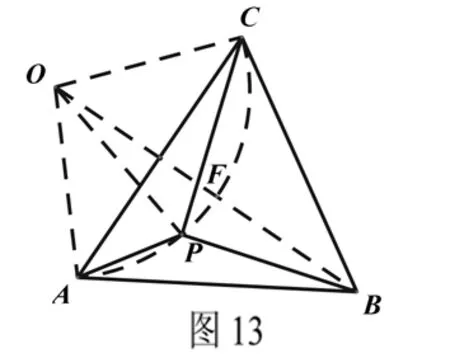
通过以上问题的探究，我们发现基础知识是学生解决数学问题的最基本要素。在教学中，教师要善于引导学生发现动点题目中不变的量，不变的性质和不变关系。对于求解一条线段长的最值问题学生常常会发现点的运动轨迹是一个隐形的圆。教师要引导学生抓住图形的这一几何特征，依据“圆内(外)一点到圆上各点的连线中，点与过圆心的直线与圆近交点距离最短，远交点距离最长”这一基本解题模型，通过以静制动，多解归一的方法来求得线段长的最大或最小值。