在数学教学中培养学生“问题发现”能力的实践研究
2019-03-26裴建平
裴建平
一、研究背景
新的课程改革倡导数学素养教育,《普通高中数学课程标准(征求意见稿)》指出:“数学核心素养是数学课程目标的集中体现,是在数学学习的过程中逐渐形成的。”数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的思维品质与关键能力。面对未来,教育应该赋予学生的到底是什么?在回答“学什么”之前更应该思考的是,学生在学习了各学科课程后,到底留下了什么? 由此,只注重知识和技能的教学已经不再符合新的课改要求,教师在教学中还要注重培养人的问题。教师对学生“问题发现”能力的培养是至关重要的一个方面。
二、数学学科“问题发现”能力的概念及意义
数学问题发现能力是指在学习数学的过程中产生一种发现问题的意识,进而形成一种学习能力。培养学生数学问题发现能力就是要在教学过程中注重创设自由、民主、开放的教学环境,鼓励学生自己主动地发现自己知识结构中的疑点和盲点,通过观察学习、推理思考,充分发挥自己内心的好奇心,挖掘探究知识的本质。
爱因斯坦曾经说过:“提出一个问题比解决一个问题更为重要。”因为解决问题仅是学习上或实验上的技能而已,而提出新的问题、新的可能、从新的角度去看旧的问题却需要创造性的想象力。世界上许多创造都源于“问题”,“问题”是开启创新之门的钥匙。一个人善于动脑、善于思考就会不断发现问题、提出问题。
希尔伯特指出:“只要一门科学分支能提出大量的问题,它就充满生命力;而问题缺乏则预示着独立发展的衰亡或终止。”例如:“平行公理能否证明?”的问题将数学研究引入了非欧几何的新天地;“高次方程有没有求根公式?”的问题导致了群论的诞生。因此,问题是学习的动力与向导。问题使人的注意力具有明显的指向性与选择性,对持续进行有目标的思维探索活动具有明显的激励功能。
美国布鲁巴克认为:最精悍的教学艺术,遵循的最高准则就是让学生自己提出问题。
在我国,大教育家孔子认为“疑是思之始,学之端”,提出“疑思问”的主张。陶行知先生曾说过,创造始于问题,学则生疑,疑则学进。
三、在课堂教学中培养学生“问题发现”能力的教学策略
1.在新授课中引发学生提出问题
教师在备课时,所备的内容在常规的备教材、备学生的基础上,可以在适合的知识点处设计教学环节引发学生提出问题。
【案例1】高一年级必修1《函数的单调性》
笔者设计了2个环节培养学生的问题意识。
环节一:在引出单调性的定义之前,先让学生结合图像回忆初中所讲的函数增减性的知识。然后屏幕中打出最关键的一行文字“y随x的增大而增大”。进而,提问“对于这句话,你能提出哪些问题?”(设计问题一)。
教学预期目的:希望学生能理解3种数学语言的表达。这是数学表达中的文字语言,图形语言前面也见到了,那么接下来需要思考的就是符号语言该怎样表示呢?从而引出单调性的定义。
环节二:当函数的单调性概念明确以后。并不是直接进行例题的讲解,而是增设初高中2个概念对比的环节。屏幕上同时打出了初中概念和高中概念。初中概念:从左至右图像上升,y随x的增大而增大;高中概念:函数y=2x在(-∞,+∞)上是增函数;在(-∞,+ ∞)区间是函数y=2x的增区间。
然后提出问题:“对比两种概念,你能提出哪些问题?”(设计问题二)。
教学预期目的:笔者设计此环节一方面希望学生明确对于确定的函数y=2x就初高中概念进行对比,能够发现异同点,引发学生理解高中概念里面数学抽象符号语言的精炼美;另一方面,希望学生能够学会发散思维,提出问题:如换一个减函数,相应的表达是怎样的?进而学生能够辨证看待问题,如把区间去掉,或者把区间范围缩小可以吗?
既然是期待学生提出问题,所以肯定学生不会像回答简单的是与否类的问题那样,答案有着很大一致性,学生对于提出问题的回答会是各种各样的猜想和疑问。因此,教师设计的问题如果太宽泛,学生的思维会信马由缰,不知道怎样提问才好;如果问题太狭窄,又不能很好激活学生的思维。所以,能引发学生提出问题的教学不是很轻松就能完成的事情。教师的设计既要针对问题,也要针对学生的掌握程度,既不能太宽泛,也不能太狭窄。对于学生提出问题的解答,形式更是灵活多变,教师可以直接明确给出答案;也可以就学生的问题再次进行学生间的讨论,使得真理越变越明;还可以留待学生课下查阅资料,进行拓展性学习等。
在新授课中,学生逐渐学会带着“问题发现”的意识进行学习,不仅能够更深刻领会所学知识,而且更重要的是学会寻找知识之间的关联点,自己学会探索未知领域。
2.习题课中引发学生提出问题串
在教学中离不开的就是题目讲解,知识和方法的展现也是通过具体题目为载体实现的。给学生讲题时,该怎样讲,有着很深的玄机。此时更是培养学生问题发现能力的最好时机。
【案例2】2015年北京文科卷第三题:下列函数中为偶函数的是( )
A.y=x2sinxB.y=x2cosx
针对本题,首先设计的5个方面问题串如下:
(1)什么是偶函数?
(2)怎样判断一个函数是偶函数?
(3)解析式有怎样的结构可以是偶函数?
(4)图像变换的类型有哪些?
(5)基本初等函数怎样组合可以成为偶函数?
随着问题得以解答,学生思路也得以清晰。然后,教师再指导学生模仿练习提问,给出下面的例题。
A 是偶函数,且在R上是增函数
B 是奇函数,且在R上是增函数
C 是偶函数,且在R上是减函数
D 是奇函数,且在R上是减函数
学生提出的问题串如下:
(1)函数解析式是怎样构成的?定义域和值域是什么?
(2)函数图像是什么?
(3)怎样判断此函数是奇函数还是偶函数?
(4)什么是奇函数?偶函数?增函数?减函数?
(5)怎样判断此函数的单调性?
(6)把函数解析式中的减法运算改换成其它运算,如加法、乘法、除法运算,函数的性质是怎样的?
......
这样的策略培养,教师有意引导,学生一段时间积累锻炼之后,形成一种习惯状态,养成在思考的过程中提出问题的好习惯。
【案例3】函数y=-x2+1,,-1<x<2的值域是 ( )
A (-3,0] B (-3,1] C [0,1] D [1,5)
对于这道题,教师引导学生提出问题,如:
(1)函数求值域的方法有哪些?
(2)本题用哪种方法解答更简洁?
(3)本题的函数图像是怎样的?
随着每一个问题的解答,本题得以正确求解,接下来,教师并不是就此放过本题,开始下一道题的练习,而是进行更深入一步的教学设计:有意引导学生对本题学会变式提问:本题可以在哪些方面进行变化?
一题多变的形式可以引发如下5个方面的思考。
(1)变求值域为求函数的单调区间?求函数的零点?……
(2)变给定的x的范围,题目的答案是怎样的?
学生可以进行以下的变化:①-1≤x≤2② -1≤x<2③-4<x<2④-4<x<-2⑤2<x<4⑥a<x<a+1……
学生改变x取值范围的各种情况,教师再进行适当补充,主要是改变边界的取值、不等号、边界的具体数为参数等,引发学生理解函数单调性是解决值域的关键所在。
(4)改编成逆向思考的问题可以怎样设计问题呢?
引导学生在本题的基础上进行自编题目设计,如:
f(x)=-x2+1,对于任意x∈(-1,2),f(x) ≤a恒恒成立,求a的取值范围。
(5)函数的解析式可以怎样变化呢?
可以设计变化如:
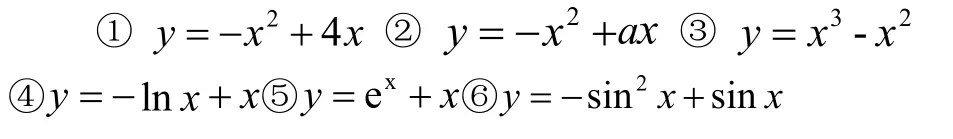
……
对于提出的问题,教师再进一步引导学生解决问题,探求解决问题的多种途径。学生不再是简单地做题,教师也不是停留在简单讲题的阶段。对于问题进行变式分析和思考以后,学生的学习成绩提高显著,学习热情得以很好的激发。
四、结语
在数学教学中,坚持培养学生的“问题发现”能力,学生提高的不仅仅是成绩,对于学习观念、学习方法方面也有很大提升,学生不再是仅仅限于机械式学习,而是在学习之中能自己能主动发现问题、提出问题,再进一步解决问题,最终学生的数学素养得以培养!
