温度与占压综合作用下埋地含缺陷聚乙烯管道数值分析

陈国华，王 番，李明阳，周池楼，廖志雄，刘圣平

(1.华南理工大学安全科学与工程研究所，广州 510640；2.广东省特种设备检测研究院珠海检测院，广东 珠海 519002； 3.广东省特种设备检测研究院云浮检测院，广东 云浮 527300；4.广东省特种设备检测研究院河源检测院，广东 河源 517000)

0 前言

聚乙烯管由于比金属管材更低廉的材料、安装和维护费用，更好的抗腐蚀性能，更小的表面摩擦力以及更佳的抗变形、抗震能力，自20世纪60年代末问世以来在燃气管网中的占比呈指数函数的趋势上升[1]。随着城镇化的快速进行，在快速扩张的过程中因施工扩建等行为产生很多堆载、临时堆积等占压活动，造成占压区域的局部变形和应力集中，严重时更会影响到管道的正常服役过程，造成管道破裂甚至引发事故灾难和人员伤亡[2]。

根据国内外管道的失效原因统计，燃气管线违章占压是仅次于第三方破坏以及施工与材料缺陷的主因之一。“7·28”地下管道爆燃事故与“11·22”中石化青岛管道爆炸事故的事故报告中，均指出管道占压问题是造成事故发生的间接原因之一，因此有必要对占压载荷开展进一步深入分析。

对占压载荷作用下埋地管道分析，国内外也进行了一系列研究。CHIOU等[3]对埋地管线在占压破坏作用下的梁屈曲模式和局部壳屈曲模式及其相互影响进行了数值研究；帅健等[4]分析了X65钢材在占压下管道的纵向位移、环向应力云图，并探讨了各因素对管道位移以及内外壁环向应力差的影响；Tafreshi等[5-7]通过实验探究了动载占压下埋地聚乙烯管道受力情况的变化规律，得出管道变形的主要影响因素来源于动载荷的第一次施加；郑津洋等[8]通过实验得到管材的本构方程并进一步得出PE管的屈服应力，在此基础上分析了管道在占压作用下的应力变化过程以及占压尺寸对应力值的影响。

关于占压载荷下埋地管道的研究主要集中在钢制管道，对于聚乙烯管道的研究还相对较少，而随着现阶段聚乙烯管道的快速发展，有必要考虑聚乙烯管道的安全使用问题。目前的聚乙烯管道研究中，仅考虑了占压载荷下完好管道的应力变化情况，在实际工况中，存储、运输和敷设过程很容易在管表面造成体积型缺陷，而一些地区的温差变化也较为明显，因此温度变化以及管道缺陷可能与占压载荷同时存在[9, 10]，加剧了管道的应力破坏。基于此，本文通过ABAQUS有限元分析软件分析了温度载荷对在役含缺陷聚乙烯管应力值的影响、给定工况下缺陷位于不同位置时管道应力值随占压载荷增长的变化规律，最后探讨了埋深、占压位置、土体弹性模量、管土摩擦因数对管道力学性能的影响，可为实际工程中占压载荷对管道影响提供理论依据。

1.1 材料本构模型选取

聚乙烯作为黏弹性材料有着更加显著的率敏感性，它的材料参数随着加载速率的变化而改变。将土体上方占压视作较为长期作用的准静态过程，本文选取1×10-5/s的准静态加载速率，基于此在拉伸机上进行单轴拉伸试验并于工程应变的0.2处停止拉伸。应力-应变关系根据文献[11]所得，如式(1)所示。

(1)

式中σ——真实应力，Pa

ε——真实应变，无量纲

根据土体实际情况，在土体的内摩擦角小于22 °时，选取ABAQUS提供的扩展Mohr-Coulomb模型对土体参数进行设置，该模型的模拟效果较贴合实际情况，而且当土体承受多种载荷时该模型具有较强的适用性，在工程中得到广泛的应用及认可[12-13]。

1.2 管土接触设置

线性关系一般都是理论上的一种理想近似，因此大多外载荷与系统的响应之间都属于非线性关系，而在占压载荷作用下的管土接触分析就是典型的边界条件非线性问题，管土之间的接触面积和应力分布是随着占压载荷变化而变化的。

选取聚乙烯管的外表面作为接触主面，土体与管道接触的面为从面，在接触选择上使用有限滑移；在设置接触属性时，法向属性采用硬接触，土体与管道两接触面所传递的压力只随外载荷的变化而变化；切向属性采用库伦摩擦模型，摩擦公式选择罚函数，当模拟中的管土切应力未超过临界切应力前，管土不会发生相对滑动[14]，临界切应力(τcu)如式(2)所示：

τcu=u·p1

(2)

式中u——管土摩擦因数

p1——管土法向接触压力，Pa

1.3 温度与占压载荷施加

聚乙烯材料对温度有着很强的敏感性，且聚乙烯管材的屈服应力要远小于金属管材，因此有必要考虑温度载荷在本文中的影响。本文的热分析问题不考虑温度变化对材料参数及边界条件的影响，且温度场恒定不变[15]。在热应力分析过程中，外界环境温度的变化通过土体从管土接触面传导至聚乙烯管，再通过材料的弹性模量和线膨胀系数影响管道和土壤应力。

在有限元建模过程中，将占压载荷简化为选定区域的均布面载荷通过土体上表面施加到土体模型的自由表面上，再通过上述设定的管土接触，使得载荷对于土体产生的力学响应得以顺利传递到管道上来。

1.4 边界条件设置

由于管土模型几何特征上的对称性，本文采用1/4模型进行数值分析。边界条件的具体设置如下：模型的两个对称截面采用对称约束；管道的两端采用轴向约束；土体的上表面和未加约束的另一侧面为自由表面；土体的底部端面采用固定全约束，边界条件设置如下图1所示。

图1 管土模型边界条件设置Fig.1 Boundary condition setting of pipe-soil model

1.5 模型网格划分

在Mesh模块中将模型进行网格划分，选取修正的二次四面体单元C3D10M网格类型，能较为精确地计算管土应力情况。其中，对管道与土壤的接触面进行网格加密，以更精确地计算管道的应力变化情况，管道及土体模型的网格划分如图2所示。

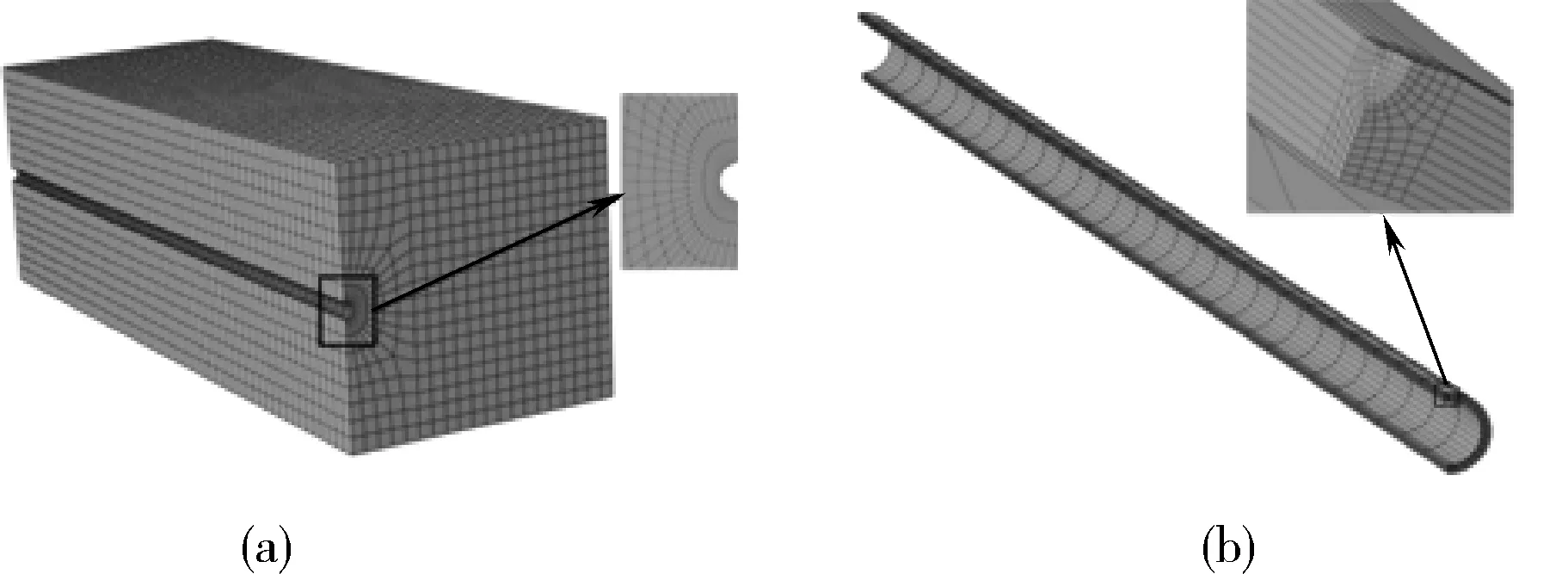
(a)土体 (b)管道图2 管土有限元模型网格划分Fig.2 Finite element model mesh generation for pipe-soil

2 有限元模拟与分析

根据上述有限元模型建立，具体参数选取如下表1、2所示。土体尺寸参数取6 000 mm×4 000 mm×1 800 mm，缺陷取聚乙烯管道常用的体积型椭球缺陷[16]，并选定几何尺寸为3 mm×3 mm×4 mm的半椭球型缺陷，管道外径为110 mm，标准尺寸比(Standard Size Ratio，SDR)为11，管长6 000 mm，管道埋深为900 mm。

表1 聚乙烯管材基本参数Tab.1 Basic parameters of polyethylene pipe

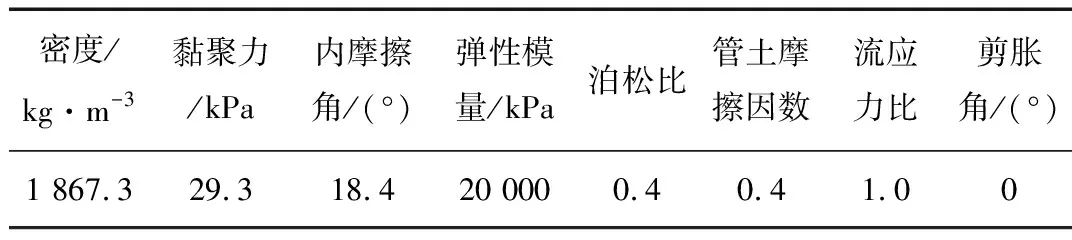
表2 土体模型基本参数Tab.2 Basic parameters of soil model

2.1 施加温度载荷必要性分析以及对管道应力值影响

先研究温度变化对于服役管道所受应力值的影响程度。分别设置15 ℃恒温、15～20 ℃温度变化、15～25 ℃温度变化、15～30 ℃温度变化、15～35 ℃温度变化、15～40 ℃温度变化6种情况，缺陷位于管道截面12点钟方向，管道最大应力随内压增大的变化情况如下图3所示。

从图3可以看出，管道处于15 ℃恒温时管道最大应力随内压的增长趋势基本呈线性关系；随着环境温度变化的影响，管道最大应力随内压的变化曲线在初期会维持在一个定值，且温差越大保持的阶段越长；随着管内压的进一步增大，管道最大应力开始逐渐上升并慢慢趋近于恒温时的变化曲线。从图中可以看出，当管内压增加至0.4 MPa时6条曲线的管道最大应力基本趋于一致，即随着管内压的逐步增大，温度载荷对管道应力值的影响也在逐渐减小。

根据《聚乙烯燃气管道工程技术规程》的相关要求，SDR11的PE80聚乙烯燃气管网的设计压力不能够超过0.5 MPa，而当管网系统中存在焊制的聚乙烯管材时工作压力不能够超过0.2 MPa，因此有必要考虑温度载荷对埋地聚乙烯管道受力的影响。

■—15 ℃恒温 ○—15～20 ℃温度变化 ▲—15～25 ℃温度变化 ▽—15～30 ℃温度变化 ◆——15～35 ℃温度变化 ☆—15～40 ℃温度变化图3 不同温差下管道最大应力值随内压变化趋势Fig.3 Variation trend of maximum stress value with internal pressure under different temperature difference

2.2 含缺陷管道最大应力随占压载荷变化规律

图4 给定工况下施加1 MPa占压载荷管道应力云图Fig.4 Stress cloud graph of pipeline with 1 MPa surface load under given working condition

基于2.1研究内容，同时考虑温度与占压载荷综合作用对管道受力的影响，以管内压0.3 MPa，环境温度变化为15～30 ℃，管道缺陷位于截面12点钟方向(管顶位置)，占压载荷从零开始施加为例，管道应力云图如下图4所示。从图可以看出，管道最大应力位于缺陷处的管道内壁，可见缺陷影响了管道的受力情况，以下探讨管道不同缺陷位置随占压载荷施加的应力变化规律。为确定管道最大应力位置，即确定3个具体方向：(1)以占压中心处为基准沿管道轴向的距离；(2)管道截面的角度位置；(3)沿管道径向(壁厚方向)的具体位置(一般只会出现在缺陷内表面或者管内壁处)。管道缺陷分别位于截面12点钟、1点钟、2点钟、3点钟、4点钟、5点钟和6点钟方向，不同缺陷位置时管道最大应力位置变化规律如下表3、4所示。

表3 管道最大应力位置变化规律Tab.3 Variation of maximum stress position in pipeline

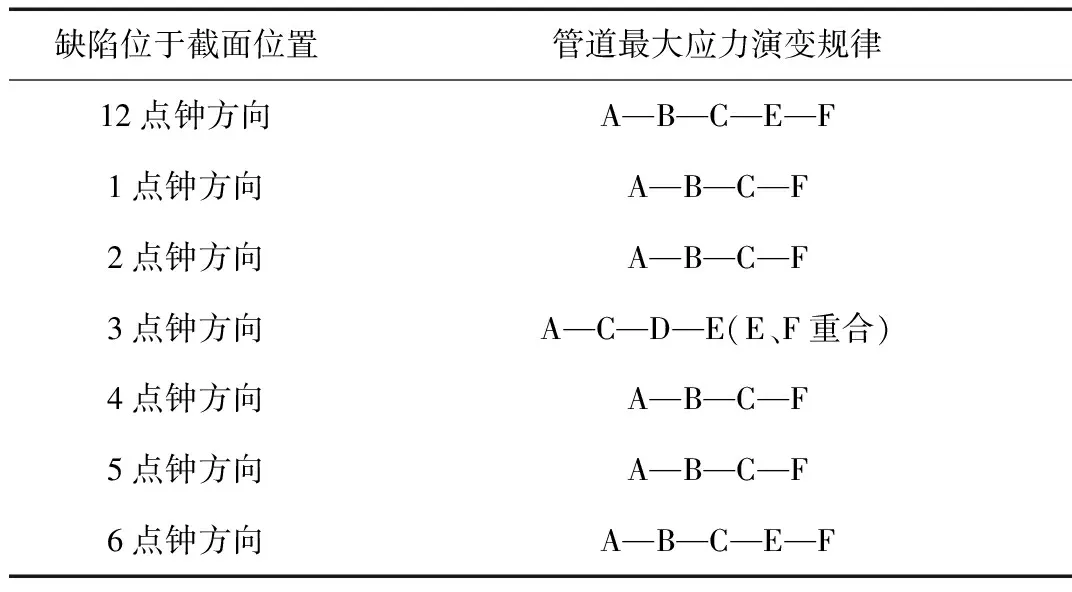
表4 不同缺陷位置时管道最大应力位置变化规律Tab.4 Variation of maximum stress position of pipeline under different defect positions

占压载荷分别从0 MPa加载至1.6 MPa，管道最大应力随占压载荷的变化趋势如下图5所示。由图5可知，内压和温度载荷的综合影响下，当占压载荷较小时，管道的最大应力先减小后增大，而当占压载荷持续增大，管道最大应力最终位于截面3点钟方向的管道内壁，这与马津津研究的完好管道最大应力随占压载荷的变化规律一致[12]。

相比管道缺陷位于其他截面角度，缺陷位于截面3点钟方向会最大程度加剧占压导致的管道屈服程度，管道更快达到该聚乙烯管材的屈服应力，造成管道变形破坏。图5可以看出，当占压载荷超过1.0 MPa时管道最大应力随占压载荷的变化规律逐渐趋于线性增长关系，此时最大应力稳定在截面3点钟方向的管内壁，当占压载荷达到约1.412 MPa时，缺陷位于截面3点钟方向时管道达到其屈服应力，管道发生屈服失效。

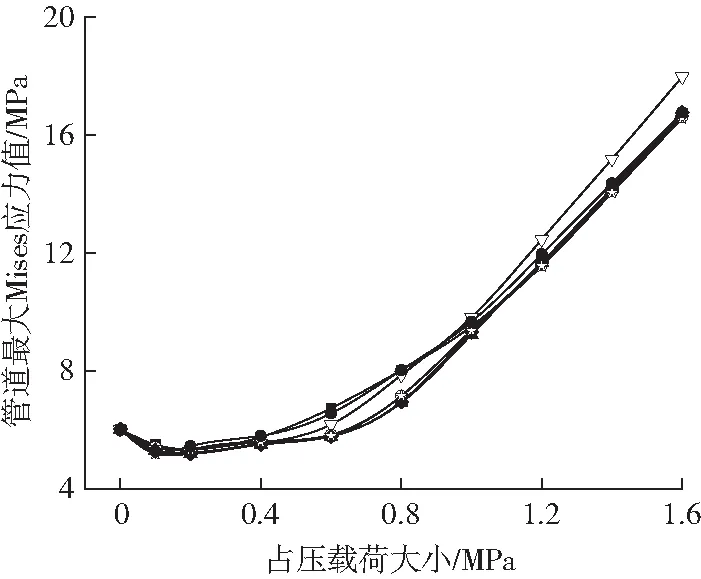
■—缺陷位于12点钟方向 ○—缺陷位于1点钟方向 ▲—缺陷位于2点钟方向 ▽—缺陷位于3点钟方向 ◆—缺陷位于4点钟方向 ☆—缺陷位于5点钟方向 ●—缺陷位于6点钟方向图5 不同缺陷位置管道最大应力随占压载荷变化趋势Fig.5 Variation trend of maximum stress with surface load in pipeline at different defect locations

2.3 不同参数对含缺陷管道受力影响分析

探讨完温度载荷以及给定工况下不同缺陷位置时占压载荷对管道受力的影响规律，分析埋深、占压位置、土体性质变化对管道受力的影响，由于缺陷位于截面3点钟方向对管道破坏影响最大，以下分析默认缺陷在此位置，工况取自上述2.2小节，占压载荷取1 MPa。

(1)埋深

《聚乙烯燃气管道工程技术规程》中明确规定埋地聚乙烯管道的最小埋深为500 mm；若管道上方为非机动车道，则不小于600 mm；若埋设上方土体为水田，则不小于800 mm；如果埋设土体上方为机动车道，则聚乙烯管的埋设深度不小于900 mm。分别设置埋深分别为500、600、700、800、900、1 000 mm的5种情况，分别计算管道的最大Mises应力。

由图6可知，当埋深从500 mm增加至1 000 mm时，管道的最大应力由24.12 MPa降至11.27 MPa，降低了53.3 %，即埋深对管道应力值的影响较大，增加埋深缓解了外载荷通过土体对于管道的传递，可以较为明显的降低占压载荷对管道的应力值。

图6 管道最大应力随管道埋深变化趋势Fig.6 Variation trend of maximum stress with buried depth of pipeline

(2)占压位置

实际工况中占压位置不一定处于管道缺陷的正上方，分别设置占压位置沿管轴向距缺陷中心距离为0、100、200、300、400、500、600、700 mm的8种情况，管道最大应力随偏移位置的变化趋势如图7所示。

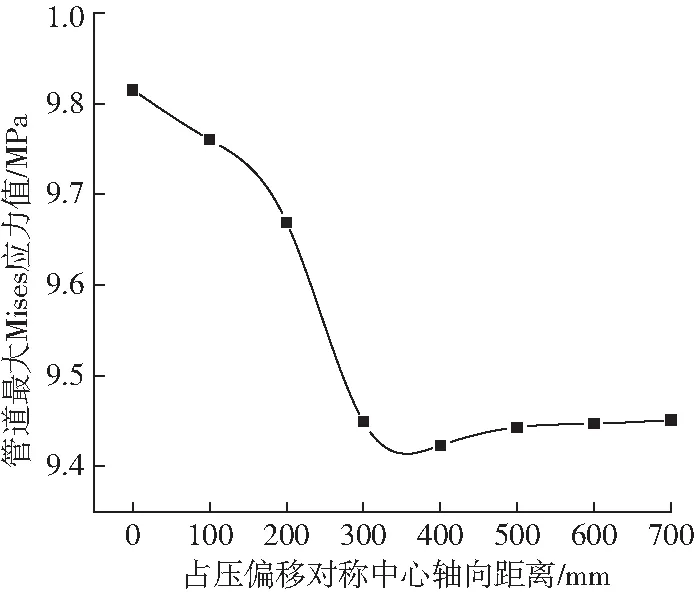
图7 管道最大应力随偏移距离变化趋势Fig.7 Variation trend of maximum stress with offset distance in pipeline

从图中可以看出，当偏移距离从0增长到300 mm时，管道最大Mises应力有一定程度下降，从9.815 MPa降至9.449 MPa，仅降低了3.2 %，此时最大应力一直位于缺陷位置处管内壁；当偏移距离增长到400 mm时，管道最大应力位置开始随占压位置发生改变，转移至占压中心的同截面，最大应力的降幅明显减缓；随着偏移距离的进一步增大，管道最大Mises应力逐渐稳定在9.45 MPa左右。可见占压载荷的大小和尺寸一定时，占压位置越靠近缺陷处管道受力越大，当偏离缺陷位置一定距离后管道受力趋于稳定，相较埋深而言占压位置的偏移对管道应力值的影响较小。

(3)土体弹性模量

弹性模量作为衡量土体疏密程度的重要参数，分别取土体弹性模量为20、40、60、80、100 MPa，管道最大Mises应力随土体弹性模量的变化趋势如图8所示。

图8 管道最大应力随夯实地基弹性模量变化趋势Fig.8 The trend of maximum stress of pipeline with the modulus of elasticity of rammed foundation

从图中可以看出，随着土体弹性模量增大管道的最大Mises应力逐渐减小，地基弹性模量从20 MPa升至100 MPa，管道最大Mises应力从23.71 MPa降至11.91 MPa，降低了49.8 %，降幅明显。占压载荷造成了土体的局部沉陷，造成管道发生局部変形进而造成应力集中，通过夯实地基可减小管土变形，管道最大应力也随之变小，因此填埋管道的土体越硬(弹性模量越大)越能起到保护管道的作用。

(4)管土摩擦因数

摩擦因数很好地反映了管土之间的接触情况，因此有必要讨论该参数对管道受力的影响程度。在0.1～0.6之间等距选取6组不同参数，模拟随着管土摩擦因数增大管道最大应力的变化趋势。从图9可以看出，当摩擦因数从0.1增至0.4时，最大应力从10.52 MPa降至9.815 MPa，随着摩擦因数继续增大，管道最大应力开始趋于平缓，摩擦因数对管道受力的影响逐渐减小，摩擦因数从0.1增至0.6，管道最大应力下降了7.4 %，总体而言摩擦因数对管道应力值影响较小。通过压实土体减小了土壤颗粒之间的孔隙距离，不仅可以增大土体弹性模量，同时也增大了管土之间的摩擦因数，从而进一步降低了管道最大应力。

图9 管道最大应力随管土摩擦因数变化趋势Fig.9 Variation trend of maximum stress of pipeline with friction coefficient of pipe-soil

3 结论

(1)在规程要求的0～0.5 MPa或0～0.2 MPa的工作压力下，不能忽略温度荷载对埋地聚乙烯管道受力的影响，原因是在0～0.4 MPa的管道内压下，不同温度的管道最大应力具有明显差异，温差越大，管道的最大应力越大；

(2)内压和温度载荷综合影响下，含缺陷聚乙烯管道的应力总体变化规律为：在占压载荷较小时最大应力先减小后增大；当占压载荷持续增大，管道最大应力最终位于内壁3点钟方向，与完好管道的最终位置相同；当缺陷位于截面3点钟方向时，管道最容易发生屈服失效；

(3)参数对管道最大应力影响程度：埋深、土体弹性模量大于管土摩擦因数、占压位置偏移距离，增加管道埋深和土体弹性模量可以明显降低管道的最大应力，而增加占压位置距缺陷中心距离和管土摩擦因数只能较小程度降低管道的最大应力，因此可适当加大埋深、压实土体(提高土体弹性模量和增加管土摩擦因数)，降低管道最大应力，为管道防护提供理论依据。