基于多源传感数据相关性分析的电厂设备故障检测方法∗

柴 政 刘 晨 朱美玲 ，3 韩燕波

（1.北方工业大学大规模流数据集成与分析技术北京市重点实验室 北京 100144）（2.北方工业大学数据工程研究院 北京 100144）（3.天津大学计算机科学与技术学院 天津 300072）

1 引言

伴随着电力系统不断的发展，发电厂设备的运行状况愈加复杂，布置在设备上的传感器产生的数据规模愈加庞大，故障原因也越来越多。依赖人工经验进行设备故障检测愈发困难，因此基于信息技术的设备故障自动检测技术越来越重要［1］。

当前，基于信息技术的设备故障自动检测方法主要利用模型对电力设备运行状况进行异常诊断，主要包括小波变换［2］、神经网络［3］、Bayes网络［4］和支持向量机［5］等。这类方法基于人工经验和历史数据，建立故障预警模型。这类方法的不足是必须要有客观的历史数据作为支撑。然而设备运行状况监测过程中的业务知识因为设备检修人员的主观理解不同而存在差异，影响了模型的准确性。

本文尝试依赖大数据分析的方法来实现电厂设备故障的在线检测。本文方法事先不关注设备的先验知识，而是通过电厂设备传感器产生的实时数据的关联变化来推测设备故障，并进行预警。然而，电厂设备上传感器数量不断增加，多个传感数据之间隐含着不易被发现的关联关系。对这些关联关系变化的检测可以帮助检修人员发现隐藏的潜在故障，尽早做出预警。由于电厂设备之间的协作关系，单个设备发生异常后会引起其他设备的异常。这种现象被称为异常的传播。这种现象将导致不同来源的相关传感数据存在时间上的延迟，即某传感数据序列延迟一段时间后与另一传感数据序列存在相关性。然而，传统的相关性分析技术不能有效地应对这种传感数据的时间延迟问题。

为此，在相关性分析研究的基础上，本文提出了一种基于皮尔逊系数的多源传感数据关联在线检测方法。其主要贡献有：1）提出了一种基于皮尔逊相关系数的聚类方法，把具有相关关系的传感聚为一类；对组内的传感利用多元线性回归建立线性模型；利用滑动窗口实现曲线的排齐，明确传感数据之间潜在的关联关系。2）提出了一种针对时间延迟的传感数据在线相关性检测算法，实时监控传感数据之间相关性的变化趋势，根据相关性的异常变化预测故障的发生。最后，通过实验验证了本文算法的有效性。

2 动机

本文的研究动机来源于某真实火电发电厂设备故障检测的实际需求。该电厂下管辖两个机组，每个机组中存在很多发电设备，每个设备上部署的传感器数量从几十到数百不等。整个发电厂共有7616个传感器。这些传感器实时监控设备的运行状态。

传感数据之间存在着许多潜在关联，其关联的变化往往预示着设备工作状态的变化，对发现设备运行的潜在故障起着关键性的作用。如图1所示，磨煤机设备在正常运行状态下磨煤机C进口一次风压和给煤机C的电流呈现线性相关。在2014-07-23 17：07：00到2014-07-24 01：05：59时间段内设备发生异常“一号炉C磨风压取样防堵吹扫装置漏气”。在此期间原有的相关性被破坏，如图1虚线框所示。而且进一步分析发现，在两条传感数据的取值并没有超出允许范围，无法利用孤立点检测等传统方法检测故障。该案例说明，发现传感数据相关性的变化对故障检测具有实际意义。

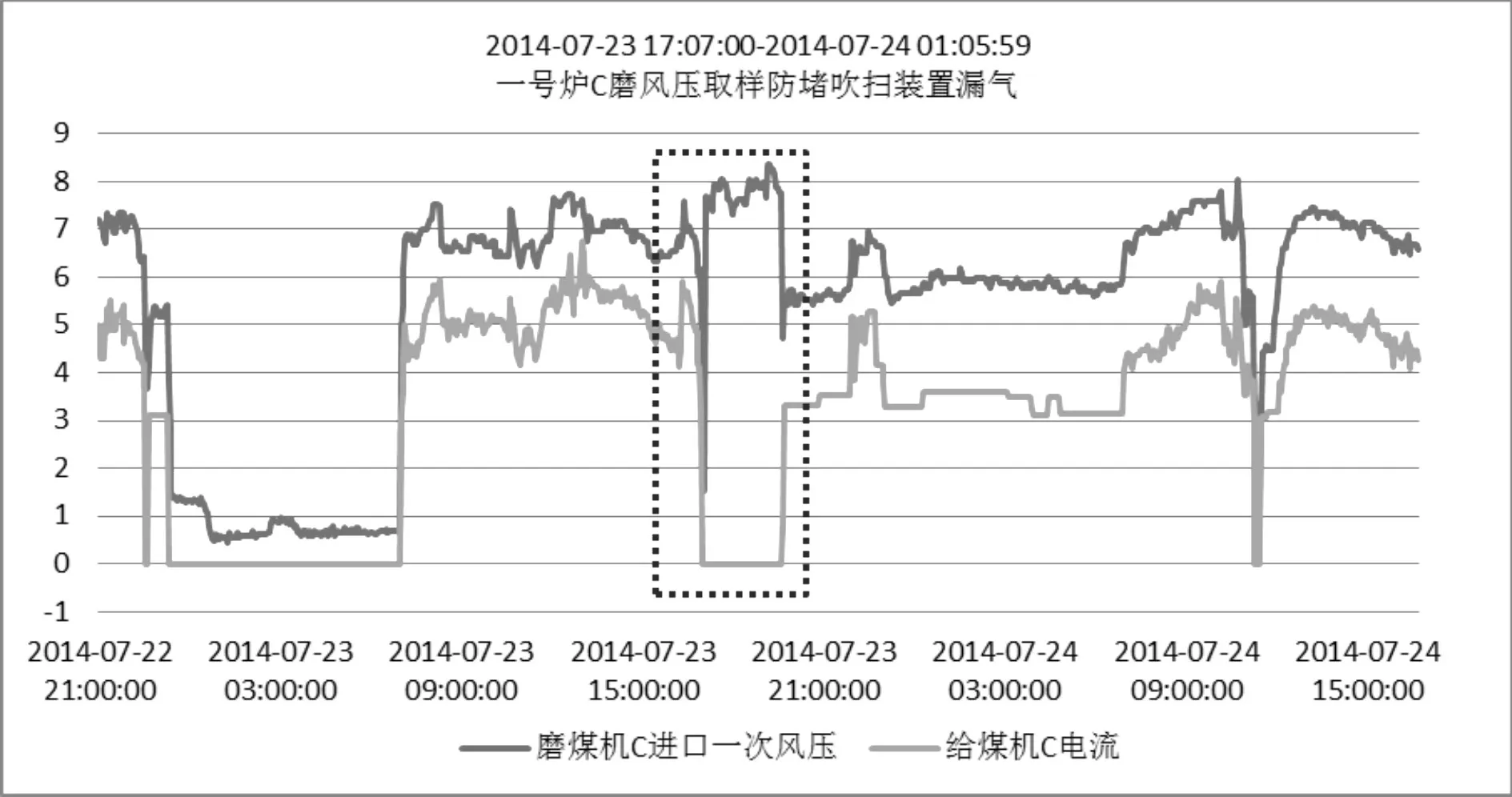
图1 关联在故障预警中的作用

为此，本文的思路是通过分析多源传感数据流之间的相关性变化来捕获数据的异常并预测设备的故障。然而，传统的相关性分析方法并不能有效求解本文的问题，因为传统方法不能有效应对多源传感数据的时间延迟问题。本文在进行相关性分析时引入了曲线排齐，不停平移相关的曲线计算相关性，最终筛选出最大的相关性作为最终结果。

本文提出的一种基于多源传感在线分析的电厂设备故障检测算法，利用皮尔逊相关系数对传感进行分类，挖掘传感数据之间的关联关系，根据关联关系的变化，对发现设备潜在的故障，给出预警事件，为电厂设备的安全运行提供决策依据。

3 故障检测方法

基于前文的文分析，本文提出了一种基于多源传感数据相关性分析的电厂设备故障检测方法，方法的基本原理如图2所示。

如图2所示，本文的方法主要分为两个模块：第一个模块利用历史传感数据进行离线的训练，主要目的是为了对输入的多个传感进行聚类，并利用多元线性回归对聚类后的测点建立线性模型，以便于计算复合相关系数并挖掘传感数据之间隐藏的相关性。第二个模块对数据流进行在线检测，利用复合相关系数，检测类中传感数据的相关性是否发生了变化，从而确定故障预警信号。

在离线训练模块中主要包含两个算法：基于皮尔逊相关系数的传感聚类算法（RCluster）和类中曲线拟合算法（LCR）。在线检测模块主要包含在线检测算法（OnlineDetection）。下面分别对这三个算法的原理和实现进行详细的描述。

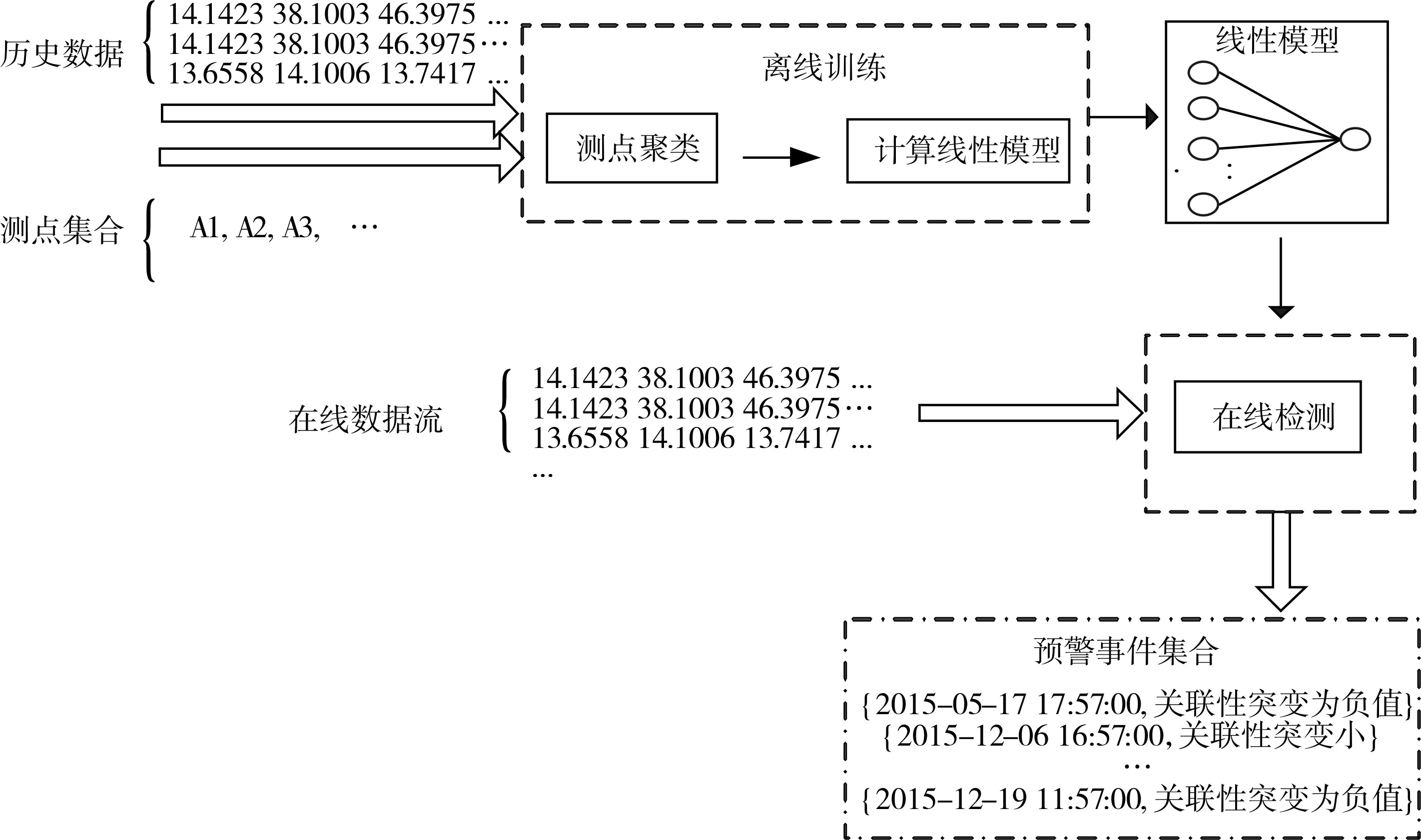
图2 在线故障检测方法框架图

3.1 基于皮尔逊相关系数的测点聚类算法

传统的聚类算法在聚类时需要给定出类别参数，即聚类结果有几类。然而在实际的故障检测中事先并不知道传感数据之间是否具有相关性，也不知道聚类的结果有几种类别。故而传统的聚类算法并不能解决本文中的聚类问题。因此本文采用了一种自底向上的聚类方法（RCluster），利用皮尔逊相关系数，计算传感数据之间的相关性，并利用传感数据之间这种模糊的相关性进行聚类。

皮尔逊相关系数是一种度量两个变量间线性相关程度常见的指标。利用皮尔逊相关系数，可以考察两组传感数据之间的线性相关程度，如果相关系数为0，则两组数据没关系，相关系数在0.00～1.00之间，两组数据正相关，相关系数在-1.00～0.00之间，两组数据负相关。

皮尔逊相关系数公式如下：

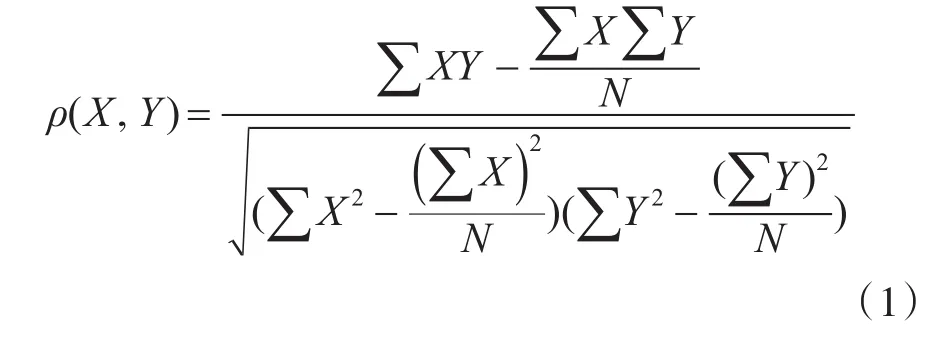
X，Y表示两组传感数据，N表示传感数据的样本数量。

给定一组传感数据样本，聚类算法利用式（1）计算每两组传感数据之间的相关系数ρ（x1，x2），判断计算出来的ρ（x1，x2）的大小，根据给定的阈值δ，如果相关系数大于δ，认为当前的两组传感数据具有很强的相关性，从而把相应的两个传感聚为一类。把与同一组传感数据具有相关性的测点聚类为一组，例如如果传感A的数据和传感B的数据之间具有相关性，传感B的数据与传感C的数据之间也具有相关性，则把传感A、B、C聚为一类。不断地对这个过程进行迭代计算，直到所有的分组之间的复合相关性很小，从而达到不同类别的传感数据之间没有相关性。

算法实现的伪代码如算法1所示。

算法1：RCluster：利用相关系数实现传感的聚类输入：

HistoryData：历史数据

Sensorlist：传感数据集合

输出：subSensor：传感聚类集合

1.JSONArray subSensor；//存储相关的传感

2.for（i=0；i＜Sensorlist.size；i++）｛

3.String name=Sensorlist.get（i）；//获取第i个传感；

4.columni=HistoryData.get（i）；//获取传感i的数据列；

5.for（j=i+1；j＜Sensorlist.size；j++）

6.columnj=HistoryData.get（j）；//获取传感j的数据列；

7.res=person（columni，columnj）；//计算两个传感的相关系数

8.IF（res＞ T ）｛

9node.put（name，Sensorlist.get（j））；//记录与当前传感具有相关性的传感

10.subSensor.add（name，node）；//分类结果

11.｝

12.｝

13.return subSensor；

3.2 组内曲线拟合算法

为了计算多组传感数据间的复合相关系数，需要对测点数据建立线性模型，计算该线性模型与第k组传感数据xk之间的相关系数，作为XK与X1，X2，…XK-1之间的复合相关系数。本文利用最小二乘法对多组传感数据进行多元线性回归，建立传感数据之间的线性模型。

线性相关模型对相关传感数据来说，可以得到很好的物理解释。例如，磨煤机的一次风流量的大小，取决于冷风调门和热风调门的开度大小，调门开大则流量增加，调门关小则流量减小。所以一次风流量信号，就可以用冷风调门开度信号和热风调门开度信号通过线性计算来拟合。

多元线性模型可以表示为

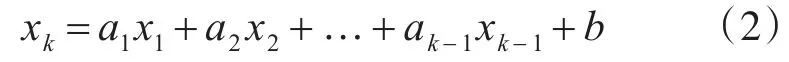
k表示组内包含的传感数目X1，…，Xk表示组内k个传感。其中a1，…ak-1是变量X1，…Xk-1的系数，b为常数。利用时间窗口记录最新一段时间内接收的实时测点数据，对时间窗口内的数据来进行线性回归训练，计算线性模型。该时间窗口随着时间推移而不断更新。每当时间窗口更新后，训练样本也相应更新，此时重新训练模型，力求寻找一组拟合度最好的线性模型。

本文为了确定XK，利用最小二乘法分别把X1，…，Xk-1作多元线性模型的因变量，剩余的k-1个传感当作自变量，进行线性回归。根据每个回归模型的复合相关系数，确定一个拟合度最好的回归模型，这个模型的因变量则为当前分组内最终确定的因变量。

算法的步骤为：1）输入组内时间窗口内的样本数据；2）利用线性回归算法计算线性模型的各个参数，确定最终的线性模型；3）更新时间窗口，迭代更新线性模型。

3.3 在线检测算法

在线检测算法主要是利用前面的传感聚类结果以及对类中传感所建立线性模型，计算组内的线性模型中的因变量Xk与其他自变量X1，…Xk-1之间的复合相关系数，判断这个复合相关系数是否发生了突变（变小或者变为负值），如果发生了突变则认为当前类中传感监测的设备发生了异常，应该给出故障预警信息。

对于线性模型，本文令

则组内的复合相关系数：

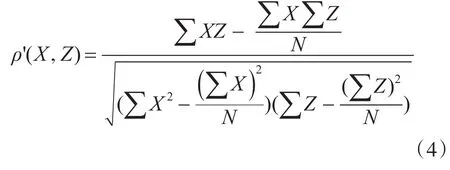
在利用复合相关系数对传感进行在线检测的时候，发现具相关传感数据存在时间延迟。为了更加准确地计算这些测点之间的复合相关系数，需要在计算之前对这些传感数据进行曲线排齐。由于并不是所有的传感数据都存在时间延迟，本文利用滑动窗口实现曲线的排齐。

具体的计算过程：1）输入线性模型的各个自变量的系数以及在线数据并读取到对应的变量下；2）设置最大的滑动窗口尺寸max，计算滑动窗口从1到max下的复合相关系数ρ'，利用冒泡排序算法找到相关系数最大的窗口大小并记录为count；3）把count下的复合相关系数ρ'与 0.1*δ做对比，如果ρ'小于0.1*δ说明类中传感的数据相关性遭到了破坏，给出预警信息。

综上所述，本文针对电厂故障的多源传感器数据检测方法的整体的算法流程如下。

1）利用RCluster算法得出测点的聚类结果，也就是传感的分组结果；

2）基于1）中的结果集，选取最近一个月内的传感数据作为样本窗口数据，对类中传感计算线性模型。每隔一段时间更新样本窗口数据，用新的窗口数据训练线性模型；

3）根据1）和2）中离线训练出的聚类结果和类中的传感模型，对于在线的数据流，实时计算组内各个传感之间的复合相关系数ρ'（X，Z），判断类中传感的相关性是否发生突变，从而给出故障预警信息。

整体算法的实现伪代码如算法2所示。

算法2（OnlineDetection）：在线检测算法

输 入 ：Sensorlist，HistoryData，OnlineData，Windowsize，count

输出：warningInfo：预警信息

1.subSensor=RCluster（Sensorlist，HistoryData）；//获取聚类结果

2.LR=MLR（subSensor，Windowsize，HistoryData）；//线性回归系数数组

3.X=ToMatrixX（OnlieData）；//把测点的数据转换成矩阵，每一列存放m-1个自变量的观察值

4.y=ToDoubleY（OnlieData）；//对因变量y进行负值

5.for（i=0；i＜=m-1；i++）

6.z+=LR［i］*x［i］//计算自变量组成的Z

7.for（count=1；count＜=max；count++）｛

8. ρ'=person（y，z+count）；//计算每个滑动窗口下的复合相关系数

9.Lρ'.add（count，ρ'）；//把每个窗口下的复合相关系数赋值到一个数组中

10.｝

11.Sortρ'=Bubblesort（Lρ'）；//对计算后的复合相关系数安从大到小的顺序进行冒泡排序

12.Max ρ'=Sortρ'［0］；//赋值复合相关系数最大的值以及当前最有效的滑动窗口尺寸

13.IF（Max ρ'.ρ'＜T*0.1）//判断复合相关系数是否发生了突变

14.warningInfo=OnlieData.time+”类中传感的数据相关性发生了突变”

15.Return warningInfo；//返回预警信息

4 实验与分析

为了有效地验证本文提出的数据驱动的电厂设备故障在线检测方法的有效性，基于真实的电厂设备传感数据，对照故障日志记录，实现第2节中的算法，确定相应的实验指标，验证方法的可行性以及有效性。

4.1 实验环境与数据

实验中采用的数据为2015年1月1号到2016年1月31号某发电厂5个设备的190个传感器产生的数据。数据的真实采集频率为每隔3分钟一次。以及在此时间范围内出现的故障次数。表1展现了数据集的具体信息。

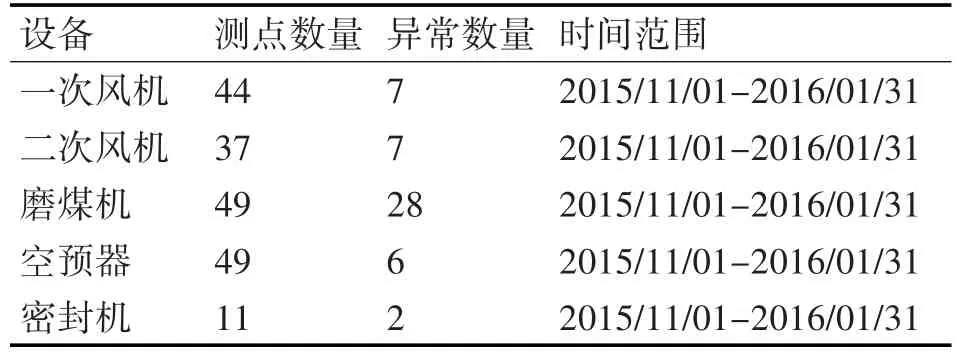
表1 实验数据集介绍

将传统的基于规则的方法与本文提出的方法进行对比。基于规则的方法是利用传感器生产时设定的阈值来判定传感数据是否异常。传感设备出产设定的阈值，通常包括传感设备的上下界限值。当传感数据超过界限值时，认为设备出现异常。

4.2 实验指标

本文将Pearson相关系数的阈值设置为0.8，即当计算的Pearson相关系数超过0.8时，认为存在相关性。

实验指标如下：准确率，衡量本文算法检测出真实异常与检测的全部异常的比例。计算公式为准确率=|真实异常∩检测到异常|/|检测异常|。另一方面，召回率，是衡量本文算法发现的真实异常与所有真实异常的比例，计算公式为召回率=|真实异常∩检测到异常|/|真正的异常|。

4.3 实验结果与分析

首先讨论方法的有效性。利用基于皮尔逊系数进行聚类的结果见表2所示。

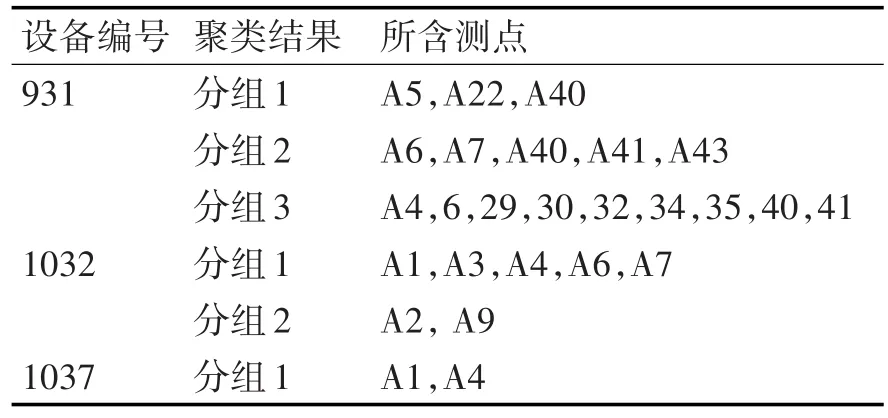
表2 聚类结果集

对各个聚类中传感的关联关系进行分析，根据关系的变化计算设备的故障预警结果集。具体结果见表3所示。

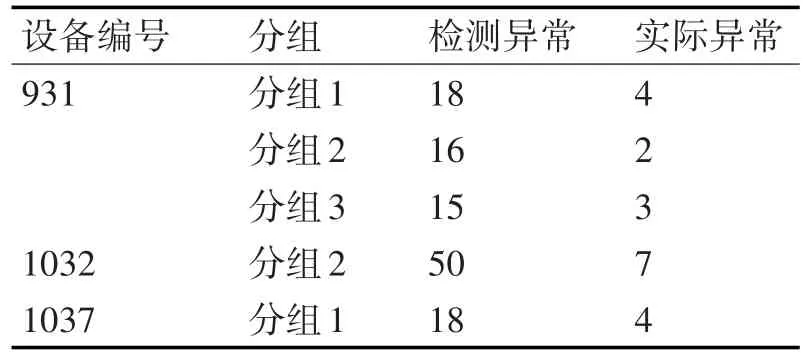
表3 故障预警结果集

如图3所示，在每个设备中，本文方法具有80%以上的准确率。五台设备检测结果的平均准确率为81.20%。对一次风机的预警结果的准确率最高，达到83%。另一方面，本文实现了基于规则的传统方法进行异常检测。基于规则的异常检测方法以电厂传感器的阈值作为判断异常的依据。当传感器数值超出阈值范围时认为设备发生异常。本节将本文方法的检测结果与该方法进行了对比。对比结果显示该方法的准确率明显低于本文方法。如图3所示，基于规则的传统方法准确率平均值为57.66%，最高值为64.52%。

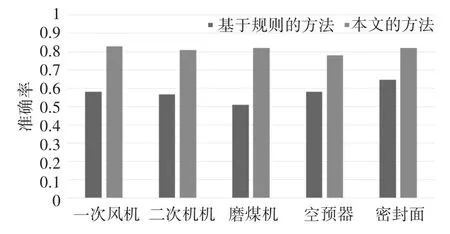
图3 基于规则的方法和本文的方法的准确度对比图

如图4所示，实验验证了在五个设备中，本文的方法比基于规则的方法检测到更多的真实故障。事实上，本文方法在每个设备上的召回率结果几乎达到90%，而基于规则的方法约为50%。这表明本文方法比传统的基于规则的方法更有效。

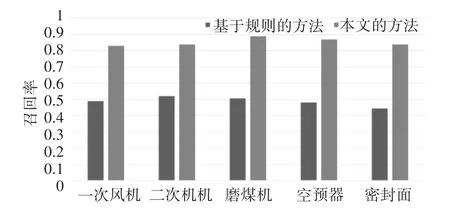
图4 基于规则的方法和本文的方法的召回率对比图

5 相关工作

5.1 相关性分析

文献［7］针对具有白噪声特性的时间序列数据流，提出一种快速检测相关性的技术，通过将草图、卷积、结构化随机向量和网格等多种数据约减技术结合起来，实现滑动窗口内高效的相关性分析。文献［8～9］提出的动态时间弯曲技术基于动态规划思想度量两组离散数据相似性的方法。文献［10］利用混合高斯分布模型对多个有关联关系的异构监控数据系统建立潜在关联关系模型，使用一个概率分布模型来检测异常。文献［11］借鉴聚类分析方法提出了一个基于相关性度量的故障检测算法（MCFD），借鉴一种改进的基于近邻的局部密度聚类分析算法来对相似的相关值的视图进行聚类，而那些不属于任何集群的异常视图就是潜在的故障传感器。文献［12］提出了基于相关分析的多元回归估计方法对无线传感器网络监测的数据序列进行相关分析，找出与当前数据相关性较强的其他历史监测数据，采用这些历史监测数据进行多元回归建模和估计。

5.2 故障检测

Santanu Das［13］针对航空数据分析提出了一种动态的数据驱动的异常检测方法，方法中实现了通过特征值提取算法来检测、分类、预测异常和故障。Osman Salem［14］使用支持向量机对医疗无线传感网中的传感数据进行分类，分出异常实例，再利用线性回归对这些异常实例定期的重建回归预测模型，判断病人传回的数据是否处于一个异常临界状态或者传感器是否读数错误。文献［15］提出了利用传感器采集的振动数据进行近似值及EMD的高铁故障诊断方法。

6 结语

本文提出的基于多源传感数据在线分析的电厂设备故障检测方法，避免了传统方法中对数据分布的已知性以及对参数设置的敏感性，完全从数据的角度出发，利用数据本身的特性，有效降低了数据分布不均对检测算法的影响。本文方法主要分为两个部分，一是利用历史数据进行离线的训练，实现对测点的聚类，并对聚类后的测点进行线性回归，建立线性模型；二是利用聚类结果和线性模型，对在线数据流进行在线的检测，找出数据层面的异常状态，从而给出对应的故障预警信息。最后本文利用电厂的实际监测数据验证分析，结果表明该算法不仅具有较高的召回率，而且本文所发现的故障时间大部分都能够早于日志记录中的故障日志时间。本文将针对如何提高准确率进行更进一步的研究与探索。